Planning motions for robots isn't too difficult if the robot is very tiny, so we can approximate it as a point. However, that's usually not the case. So a key problem in robotics is
Where can the robot move when the robot has significant size?We'll model robot and obstacles as simple geometrical shapes to develop the ideas.
Suppose that we're moving a circular robot in 2D. We can simplify planning using the following idea:
Idea: expand obstacles so we can shrink robot to a point.
This modified space is called a configuration space. It shows all the possible positions for the center of the robot.
Obstacles for a circular robot (from Howie Choset)
Another standard simple example is a robot arm with two links connected by rotating joints, like this:
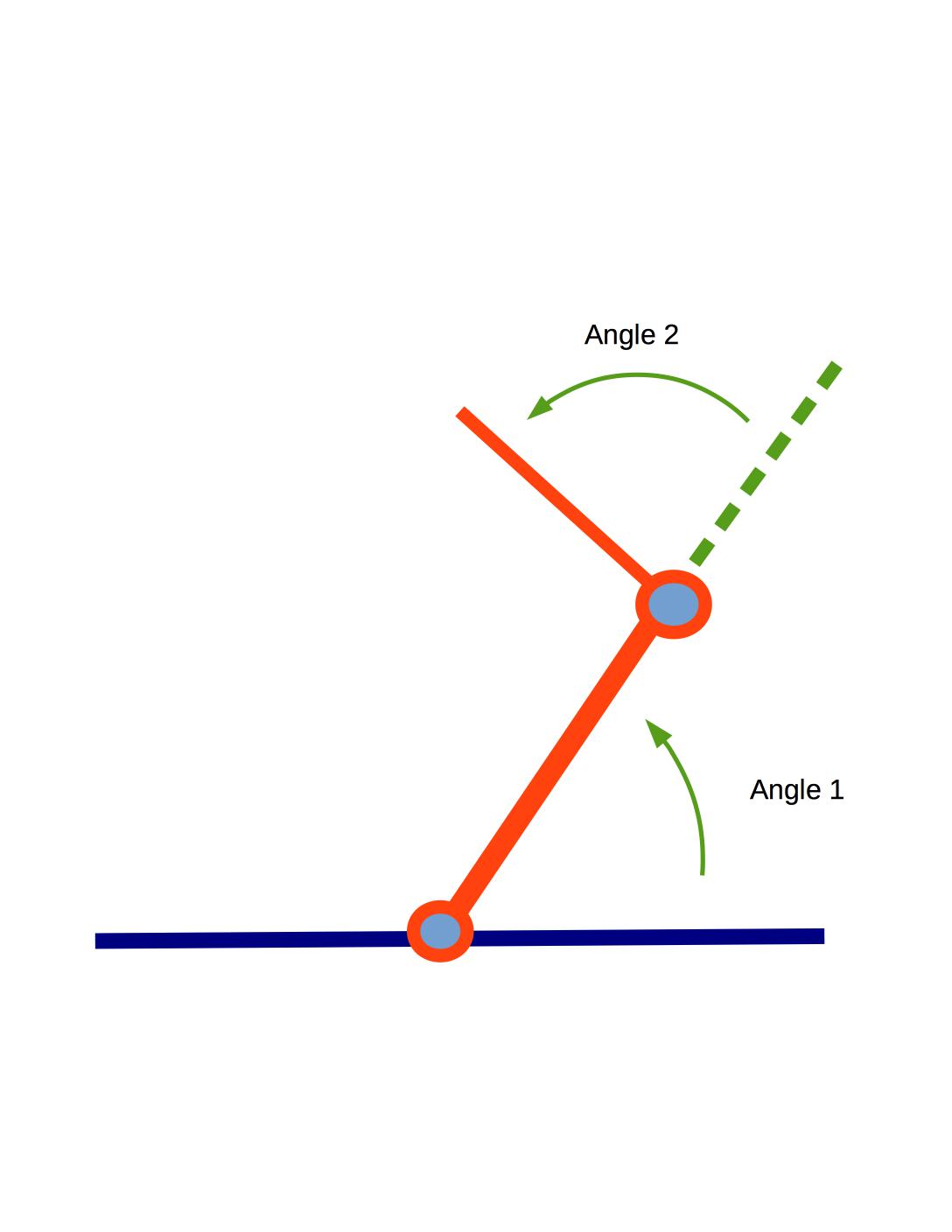
To get a sense of how the arm can move around obstacles, play around with this 2-link robot simulator by Jeffrey Ichnowski. Or look at these pictures of a physical robot model .
Our high-level planning task is expressed in normal 2D coordinates, e.g. move the tip from one (x,y) location to another. However, we control the robot via the angles of the joints. These \((\alpha,\beta)\) pairs form a different 2D space, called the configuration space of the problem:
Big idea: do planning in configuration space (Lozano-Perez around 1980).
Configuration space for a 2-link arm (from Howie Choset)
Notice that a goal in real space might correspond to more than one point in configuration space. For 2-link arm, many 2D points can be reached with the elbow pointing in two ways. For arms with more links, we can find multiple solutions to goals that specify the angle, as well as the position, of the hand. Animals can exploit this to maintain several constraints simultaneously, e.g. keep head in a fixed position while feet hold onto a moving branch.
Kingfisher video from the Audobon Society
The figures above credited to Howie Choset came from Howie Choset, CMU 16-311, Spring 2018 and 16-735, Fall 2010. For more details, check out his book Principles of Robot Motion.
Fun book on collision detection by Jeff Thompson