Homework 3 - Due: 02/08
Problem 1
Consider the following matrices:
\[ A_1 = \begin{bmatrix} 1/2 & -1/2 \\ 1/2 & -1/2 \end{bmatrix}, \qquad A_2=\begin{bmatrix}0&1\\-1&0\end{bmatrix},\qquad A_3=\begin{bmatrix}1&0&0\\0&-2&0\\-3&0&-2\end{bmatrix}. \]
- Compute \(e^{A_i t}\) for \(i=1,2,3\). Note that \(A_2\) is a special case of a matrix whose exponential was computed in class.
- For \(i=1,2,3\), write down the solution of \(\dot x=A_i x\) for a general initial condition.
- In each case, determine whether the solutions of \(\dot x=A_i x\) decay to 0, stay bounded, or go to \(\infty\) (for various choices of initial conditions).
- Try to state the general rule which can be used to determine, by looking at the eigenstructure of \(A\), whether the solutions of \(\dot x=A x\) decay to 0, stay bounded, or go to \(\infty\).
Problem 2
The pictures in this demo page show possible trajectories of a linear system \(\dot x= Ax\) in the plane, when the eigenvalues \(\lambda_1\) and \(\lambda_2\) of \(A\) are in one of the following six configurations:
| # | Configuration | # | Configuration |
|---|---|---|---|
| (a) | \(\lambda_1<\lambda_2<0\) | (b) | \(\lambda_1<0<\lambda_2\) |
| (c) | \(0<\lambda_1<\lambda_2\) | (d) | \(\lambda_1,\lambda_2=a\pm ib, \; a<0\) |
| (e) | \(\lambda_1,\lambda_2=a\pm ib, \; a=0\) | (f) | \(\lambda_1,\lambda_2=a, \; a>0\) |
Match each picture with the corresponding eigenvalue distribution. Justify your answers using your knowledge of the solution of \(\dot x = Ax\). Plotting in MATLAB or use of the demo applet cannot be used as a justification.
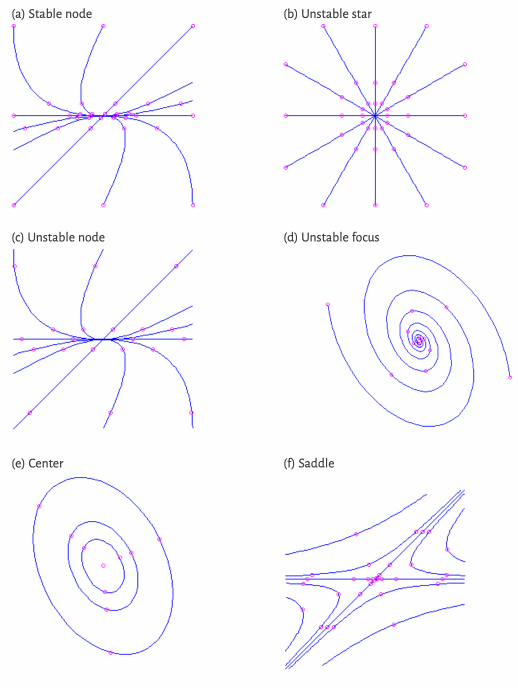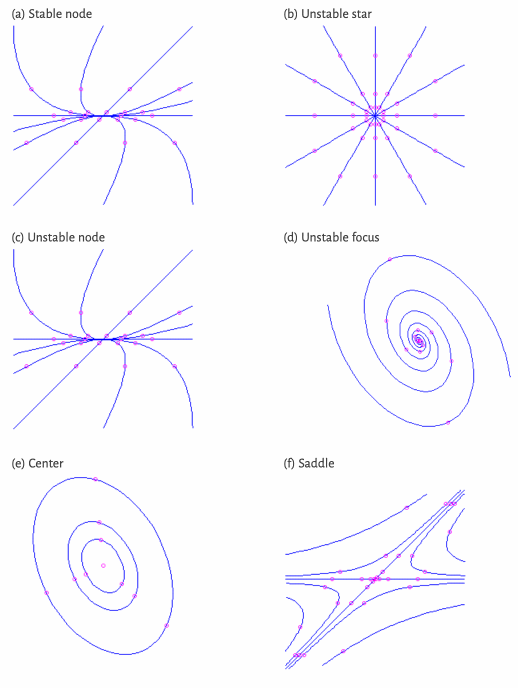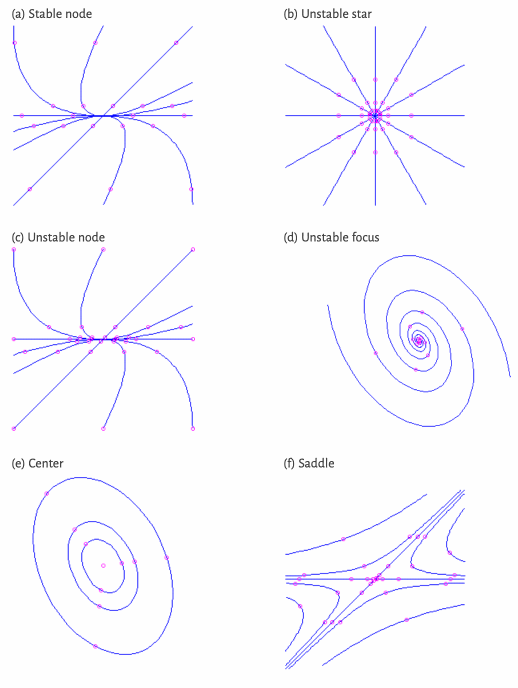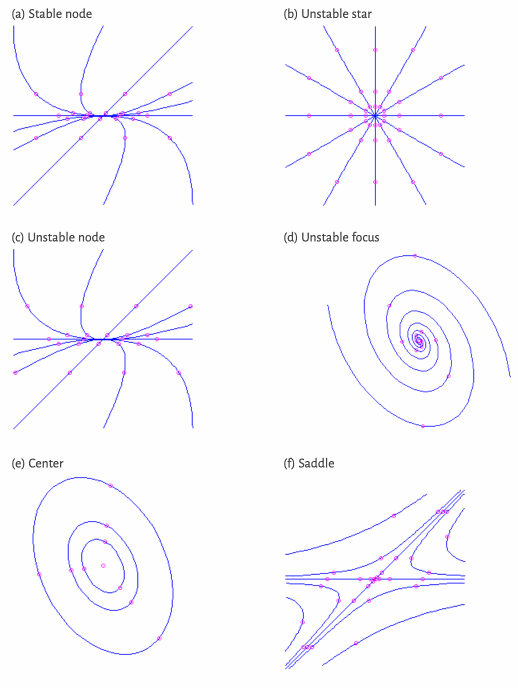
Problem 3
This exercise illustrates the phenomeom known as resonance. Consider the system
\[\begin{align*} \begin{bmatrix} \dot x_1\\ \dot x_2 \end{bmatrix} &= \begin{bmatrix} 0 & \omega \\ -\omega & 0 \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \end{bmatrix} +\begin{bmatrix} 0\\ 1 \end{bmatrix}u,\qquad y=x_2 \end{align*}\]
where \(\omega>0\), \(u\) is the control input, and \(y\) is the output. Let the input be \(u(t)=\cos\nu t\), \(\nu>0\). Using the variation-of-constants formula, compute the response \(y(t)\) to this input from the zero initial condition \(x(0)=0\), considering separately two cases: \(\nu\ne\omega\) and \(\nu=\omega\). In each case, determine whether this response is decaying to 0, bounded, or unbounded.
Problem 4
Compute the state transition matrix \(\Phi(t,t_0)\) of \(\dot x=A(t)x\) with \[A(t) = \begin{bmatrix}-1+\cos t&0 \\0&-2+\cos t \end{bmatrix}\]
Problem 5
Consider the LTV system \(\dot x=A(t)x\), where \(A(t)\) is periodic with period \(T\), i.e., \(A(t+T)=A(t)\). Let \(\Phi(t,t_0)\) denote the corresponding state transition matrix. The goal of this exercise is to show that we can simplify the system and characterize its transition matrix with the help of a suitable (time-varying) coordinate transformation.
Being a nonsingular matrix, \(\Phi(T,0)\) can be written as an exponential: \(\Phi(T,0)=e^{RT}\), where \(R\) is some (possibly complex-valued) matrix. Define also:
\[P(t):=\Phi(t,0)e^{-Rt}\]
- Using the properties of state transition matrices from class, show that \(\Phi(t,t_0)=P(t)e^{R(t-t_0)}P^{-1}(t_0).\)
- Deduce from a) that \(\bar x(t):=P^{-1}(t)x(t)\) satisfies the time-invariant differential equation \(\dot{\bar x}=R\bar x\).
- Prove that \(P(t)\) is periodic with period \(T\).
- Consider the LTV system from Problem 4 . Find new coordinates \(\bar x(t)\) in which, according to part b), this system should become time-invariant. Confirm this fact by differentiating \(\bar x(t)\).
Problem 6
Prove the variation-of-constants formula for linear time-varying control systems stated in class: \[ x(t) = \phi(t,t_0)x_0 + \int \limits _{t_0} ^{t} \phi \left(t, s \right) B(s) u(s) ds \] satisfies the LTV controlled systems’ differential equation.
Hint: Differentiate both sides. See also Class Notes, end of Section 3.7.