Homework 1 - Due: 01/25

Problem 1

Which of the following are vector spaces over \(\mathbb{R}\) (with respect to standard addition and scalar multiplication). Justify your answers.

  1. The set of real valued \(n \times n\) matrices with nonnegative entries where \(n\) is a given positive integer.
  2. The set of rational functions of the form \(\dfrac{p(s)}{q(s)}\) where \(p\) and \(q\) are polynomials in the complex variable \(s\) and the degree of \(q\) does not exceed a given fixed positive integer \(k\).
  3. The space \(L^2\left(\mathbb{R}, \mathbb{R}\right)\) of square-integrable functions, i.e., functions \(f : \mathbb{R} \to \mathbb{R}\) with the property that

\[ \int \limits _{-\infty} ^{\infty} f^2 (t) dt < \infty \]

Problem 2

Let \(A\) be the linear operator in the plane corresponding to the counter-clockwise rotation around the origin by some given angle \(\theta\). Compute the matrix of \(A\) relative to the standard basis in \(\mathbb{R}^2\).

Problem 3

Let \(A: X \to Y\) be a linear transformation.

  1. Prove that \(\dim N (A) + \dim R(A) = \dim X\) (the sum of the dimension of the nullspace of \(A\) and the dimension of the range of \(A\) equals the dimension of \(X\)).
  2. Now assume that \(X = Y\). It is not always true that \(X\) is a direct sum of \(N(A)\) and \(R(A)\). Find a counterexample demonstrating this. Also, describe a class of linear transformations (as general as you can think of) for which this statement is true.

Problem 4

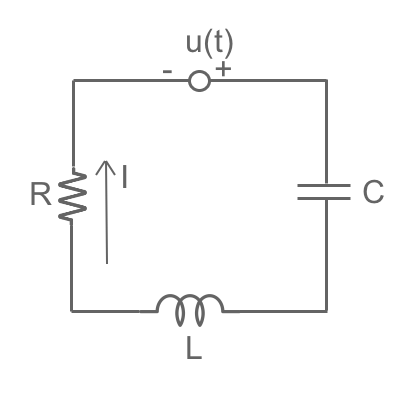
Consider the standard RLC circuit, except now allow its characteristics \(R, L\) and \(C\) to vary with time. Starting with the same non-dynamic physical laws as in class (\(q = CV_c\) for the capacitor charge, \(\varphi = LI\) for the inductor flux), derive a dynamical model of this circuit. It should take the form:

\[ \dot{x} = A(t) x + B(t) u \]

Problem 5

Three employees — let’s call them Alice, Bob, and Cheng — received their end-of-the-year bonuses which their boss calculated as a linear combination of three performance scores: leadership, communication, and work quality. The coefficients (weights) in this linear combination are the same for all three employees, but the boss doesn’t disclose them. Alice knows that she got the score of 4 for leadership, 4 for communication, and 5 for work quality. Bob’s scores for the same categories were 3, 5, and 4, and Cheng’s scores were 5, 3, and 3. The bonus amounts are $18000 for Alice, $16000 for Bob, and $14000 for Cheng. The employees are now curious to determine the unknown coefficients (weights).

  1. Set up this problem as solving a linear equation of the form \(Ax = b\) for the unknown vector \(x\).
  2. Calculate the unknown weights. It’s up to you whether you use part (a) for this or do it another way.
  3. Are the weights that you computed unique? Explain why or why not.