Remember that a queen in chess threatens another piece if there is a direct path between the two either horizontally, or vertically, or diagonally. In the n queens problem, we have to place n queens on a n by n board so that no queen threatens another. Here is a solution for n=8:
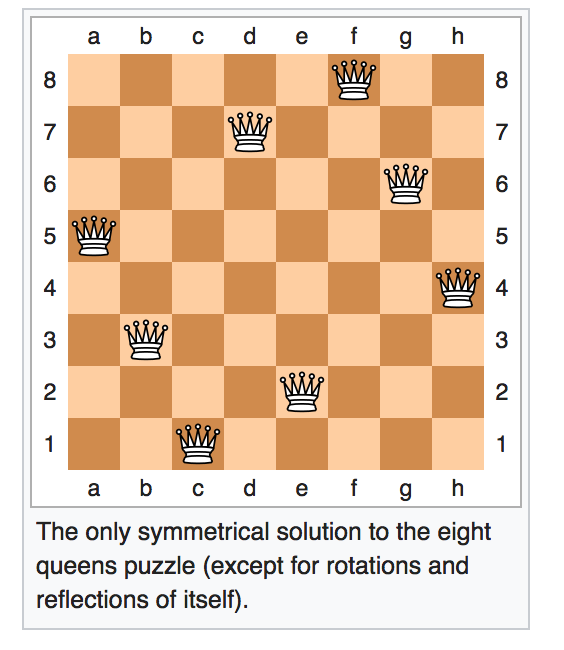From Wikipedia
Since each column must contain exactly one queen, we can model this as follows
We can visualize this as a graph in which each variable is a node and edges link variables involved in binary constraints. So X1 in the following diagram is a variable representing a column. Its possible values {1,2,3,4} are the row to place the queen in.
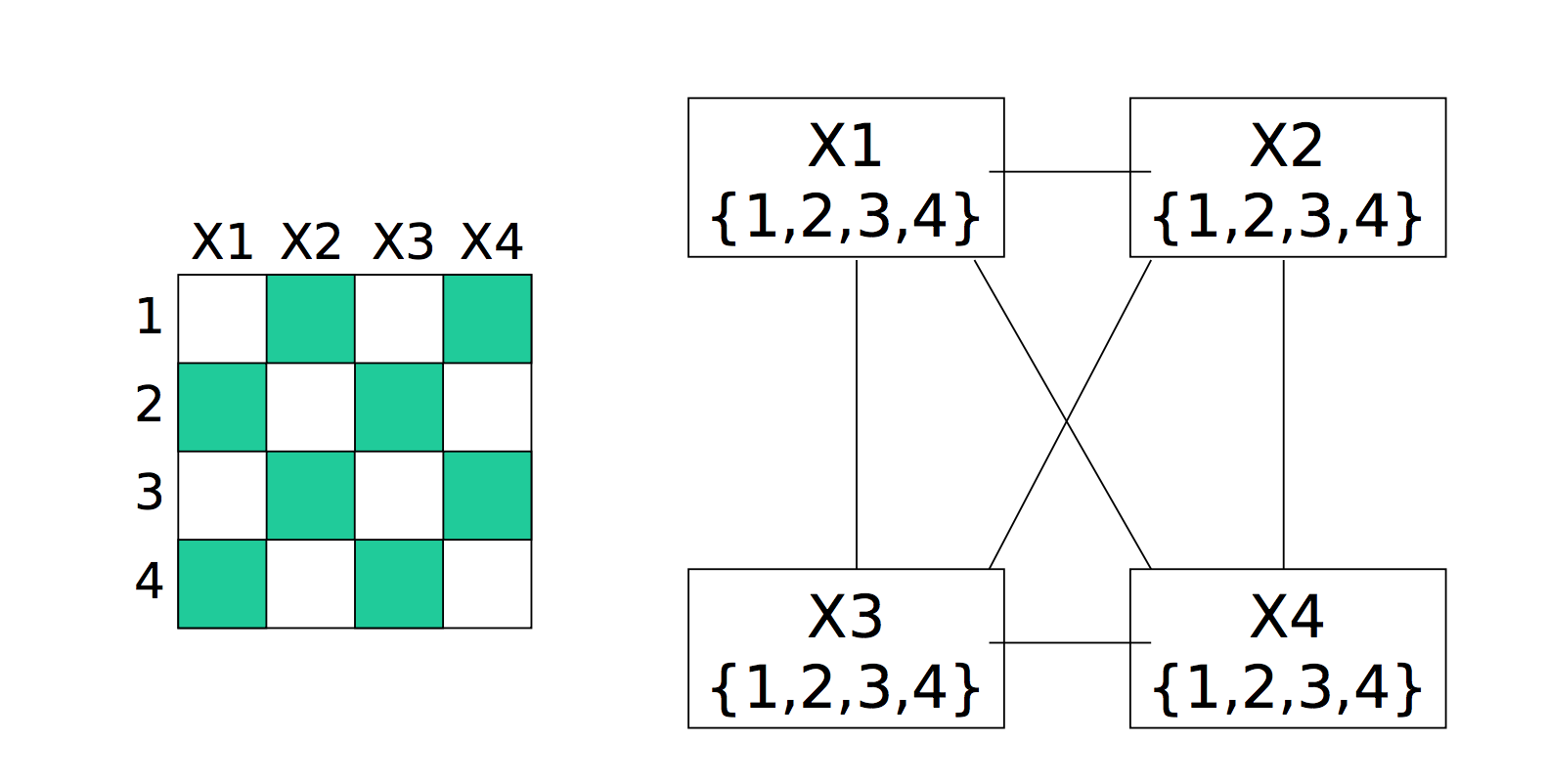
from Bonnie
Dorr, U. Maryland
(via Mitch Marcus at U. Penn).
CSP problem consists of
In many examples, all variables have the same set of allowed values. But there are problems where different variables may have different possible values.
Need to find a complete assignment (one value for each variable) that satisfies all the constraints
In basic search problems, we know the goal and want to find a path to it. In a constraint-satisfaction problem, we have only a test for whether a state is a goal. Our problem is to find a goal state. The path to the goal is only temporary scaffolding.
From
Wikipedia
Viewed as a CSP problem
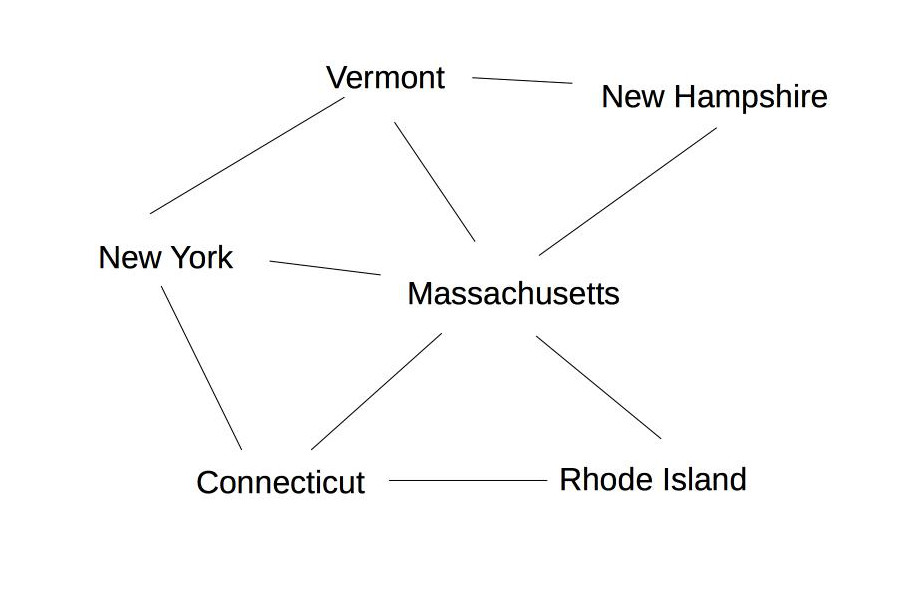
Pictured as a constraint graph: states/countries are nodes, edges connect adjacent states. Theoretical work is mostly under the keyword "graph coloring." Applications of graph coloring include register allocation, final exam scheduling.
The "4 color Theorem" states that any planar map can be colored with only four colors. It was proved at U. Illinois in 1976 and required a computer program to check almost 2000 special cases.
Notice that graph coloring is NP complete. We don't know for sure if NP problems require polynomial or exponential time, but we suspect they require exponential time. However, many practical applications can exploit domain-specific heuristics (e.g. linear scan for register allocation) or loopholes (e.g. ok to have small conflicts in final exams) to produce fast approximate algorithms.
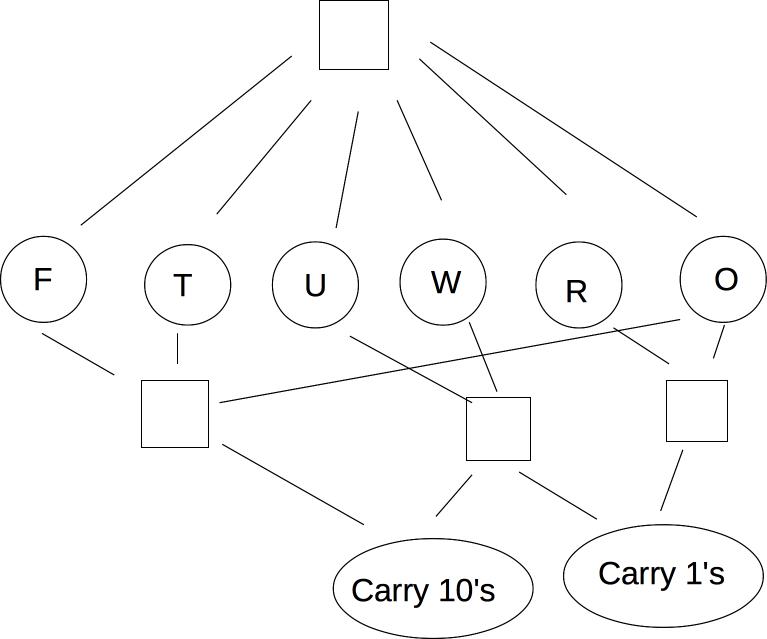
Cryptarithmetic is another classic CSP problem. Here's an example:
T W O
+ T W O
---------
= F O U R
We can make this into a CSP model as follows:
"Addition works as intended" can be made concrete with these equations, where C_1 and C_10 are the carry values.
O + O = R + 10 * C_1
W + W + C_1 = U + 10*C_10
T + T + C_10 = O + 10*F
"All different" and the equational constraints involve multiple variables. Usually best to keep them in that form, rather than converting to binary. We can visualize this using a slightly different type of graph with some extra nodes:
from
Wikipedia
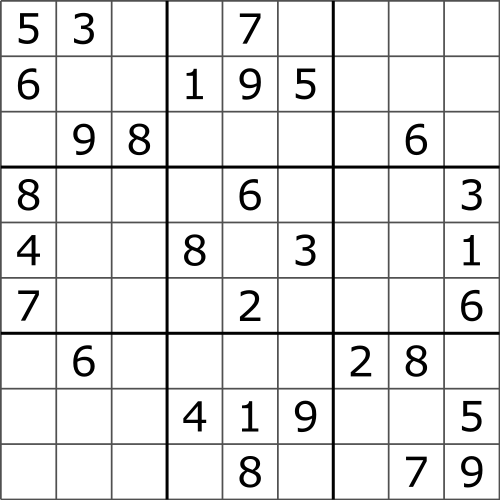
Sudoku can be modelled as a CSP problem,
We can also use this framework to model scheduling problems, e.g. planning timing and sequence of operations in factory assembly.
More CSP examples can be found at the CSPLib web page.
CSP is a search problem, similar to the ones we saw earlier in the term. For example, we can set up search as follows:
However, CSP search has some special properties which will affect our choice of search method. If our problem has n variables, then all solutions are n steps away. So DFS is a good choice for our search algorithm.
We can use a very stripped down DFS implementation, without explicit loop detection. This can be made to use only a very small amount of memory. In this type of AI context, DFS is often called "backtracking search" because it spends much of its time getting blocked and retreating back up the search tree to try other options.
A variety of other heuristics can be used to speed up CSP search. Let's start by looking at when to detect that our path is failing and we need to backtrack.
Stupid method: Always go down n levels to create a complete solution. Then check if it meets the constraints. If not, retreat back up the DFS search tree.
Smart method (forward checking): During search, each variable keeps a list of its possible values. At each search step, remove values from these lists if they violate constraints, given the values we've already assigned to other variables. Back up if any variable has no possible values left.
See this little demo of solving the 4-queens problem (from Bonnie Dorr, U. Maryland, via Mitch Marcus at U. Penn.)
We can do better than forward checking. When a value is chosen for a node X, forward checking looks for updates to the value sets for X's neighbors. Constraint propagation continues looking for updates, moving outwards from X until it runs out of changes to make. We'll see the details next class.
Constraint propagation was developed by David Waltz in the early 1970's for the Shakey project. The original task was line labelling (from Lana Lazebnik based on David Waltz's 1972 thesis). This contemporary video of a line labeller shows how constraint propagation can sometimes nail down the exact solution without any search. A more typical approach is to use a combination of backtracking search and constraint propagation.
Google's assistant demo: was it faked? was it ethical?
People are overly willing to trust robots if they claim to be making deliveries: summary, full details at Serena Booth et al. "Piggybacking Robots" (use the university's network or VPN so you can access the pdf).