Graphs and Markov chains

Learning Objectives

Graphs

Undirected Graphs:

The following is an example of an undirected graph:

The adjacency matrix, \({\bf A}\), for undirected graphs is always symmetric and is defined as:

\[a_{ij} = \begin{cases} 1 \quad \mathrm{if} \ (\mathrm{node}_i, \mathrm{node}_j) \ \textrm{are connected} \\ 0 \quad \mathrm{otherwise} \end{cases},\]

where \(a_{ij}\) is the \((i,j)\) element of \({\bf A}\). The adjacency matrix which describes the example graph above is:

\[ {\bf A} = \begin{bmatrix} 0 & 1 & 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 \end{bmatrix}.\]

Directed Graphs:

The following is an example of a directed graph:

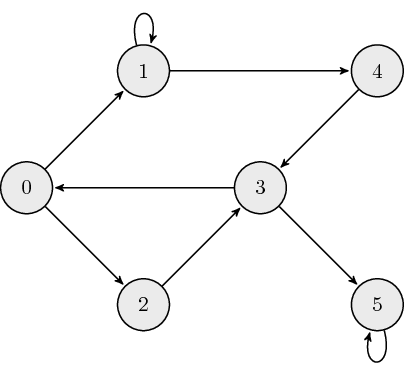
The adjacency matrix, \({\bf A}\), for directed graphs is defined as:

\[ a_{ij} = \begin{cases} 1 \quad \mathrm{if} \ \mathrm{node}_i \leftarrow \mathrm{node}_j \\ 0 \quad \mathrm{otherwise} \end{cases}, \]

where \(a_{ij}\) is the \((i,j)\) element of \({\bf A}\). The adjacency matrix which describes the example graph above is:

\[ {\bf A} = \begin{bmatrix} 0 & 0 & 0 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 \end{bmatrix}.\]

Weighted Directed Graphs:

The following is an example of a weighted directed graph:

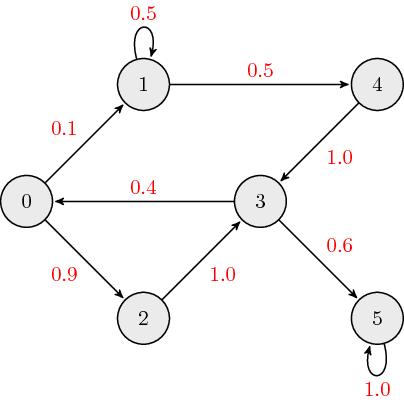
The adjacency matrix, \({\bf A}\), for weighted directed graphs is defined as:

\[ a_{ij} = \begin{cases} w_{ij} \quad \mathrm{if} \ \mathrm{node}_i \leftarrow \mathrm{node}_j \\ 0 \quad \ \ \mathrm{otherwise} \end{cases}, \]

where \(a_{ij}\) is the \((i,j)\) element of \({\bf A}\), and \(w_{ij}\) is the link weight associated with edge connecting nodes \(i\) and \(j\). The adjacency matrix which describes the example graph above is:

\[ {\bf A} = \begin{bmatrix} 0 & 0 & 0 & 0.4 & 0 & 0 \\ 0.1 & 0.5 & 0 & 0 & 0 & 0 \\ 0.9 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1.0 & 0 & 1.0 & 0 \\ 0 & 0.5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0.6 & 0 & 1.0 \end{bmatrix}.\]

Typically, when we discuss weighted directed graphs it is in the context of transition matrices for Markov chains where the link weights across each column sum to \(1\).

Markov Chain

A Markov chain is a stochastic model where the probability of future (next) state depends only on the most recent (current) state. This memoryless property of a stochastic process is called Markov property. From a probability perspective, the Markov property implies that the conditional probability distribution of the future state (conditioned on both past and current states) depends only on the current state.

Markov Matrix

A Markov/Transition/Stochastic matrix is a square matrix used to describe the transitions of a Markov chain. Each of its entries is a non-negative real number representing a probability. Based on Markov property, next state vector \({\bf x}_{k+1}\) is obtained by left-multiplying the Markov matrix \({\bf M}\) with the current state vector \({\bf x}_k\).

\[ {\bf x}_{k+1} = {\bf M} {\bf x}_k \]

In this course, unless specifically stated otherwise, we define the transition matrix \({\bf M}\) as a left Markov matrix where each column sums to \(1\).

Note: Alternative definitions in outside resources may present \({\bf M}\) as a right markov matrix where each row of \({\bf M}\) sums to \(1\) and the next state is obtained by right-multiplying by \({\bf M}\), i.e. \({\bf x}_{k+1}^T = {\bf x}_k^T {\bf M}\).

A steady state vector \({\bf x}^*\) is a probability vector (entries are non-negative and sum to \(1\)) that is unchanged by the operation with the Markov matrix \(M\), i.e.

\[ {\bf M} {\bf x}^* = {\bf x}^* \]

Therefore, the steady state vector \({\bf x}^*\) is an eigenvector corresponding to the eigenvalue \(\lambda=1\) of matrix \({\bf M}\). If there is more than one eigenvector with \(\lambda=1\), then a weighted sum of the corresponding steady state vectors will also be a steady state vector. Therefore, the steady state vector of a Markov chain may not be unique and could depend on the initial state vector.

Markov Chain Example

Suppose we want to build a Markov Chain model for weather predicting in UIUC during summer. We observed that:

The state diagram is shown below:

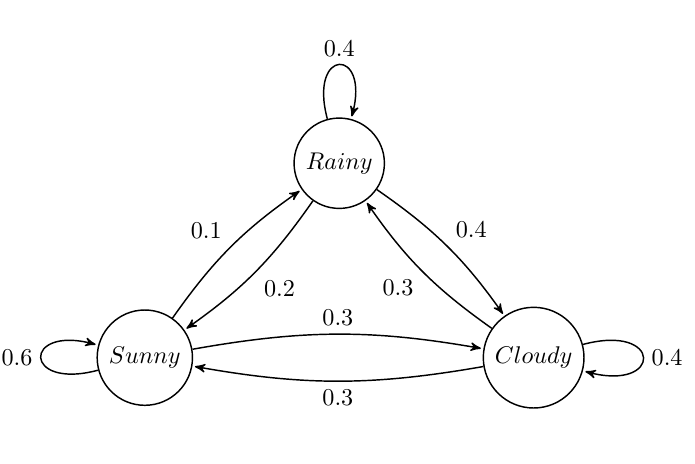
The Markov matrix is

\[ {\bf M} = \begin{bmatrix} 0.6 & 0.2 & 0.3 \\ 0.1 & 0.4 & 0.3 \\ 0.3 & 0.4 & 0.4 \end{bmatrix}. \]

If the weather on day \(0\) is known to be rainy, then

\[ {\bf x}_0 = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}; \]

and we can determine the probability vector for day \(1\) by

\[ {\bf x}_1 = {\bf M} {\bf x}_0. \]

The probability distribution for the weather on day \(n\) is given by

\[ {\bf x}_n = {\bf M}^{n} {\bf x}_0. \]

Review Questions

ChangeLog