ECE 486 Control Systems
Lecture 2

[486 Home]
Prev	ECE 486 Handbook (from Fall 2019)	Next

State-Space Representation of a System

State-Space Model – a Unified Framework

Recall from last time, we introduced the basic concept of control diagram, where the terminology we used include

System input ( $R$ )
System output ( $Y$ )
Controller block ( $C$ )
Plant block ( $P$ or $\tilde{P}$ for plant and actuator combined)
Feedback loop ( $F$ )

We also discussed the situation where the controller gain $C$ (at the moment proprotional gain only) is large, we can achieve since $C \to \infty$ implies $Y \to R$ . At the same time, the contribution of disturbance inputs $D_1$ and $D_2$ to the system output is minimal, we call it good disturbance rejection.

Now for a brief moment, we will look at another way of describing system dynamics – the state-space model. First off, a few quick examples.

Example 1: Consider the Mass-Spring system as in Figure 1. Derive the governing differential equation and rewrite it in matrix form by reducing a higher order ODE to a set of first order ones.

Correction: The displacement $x$ in the figure should be interpreted as measured against the resting position ( $x = 0$ ) of the spring, not against the wall. Since a spring can be stretched also compressed.

Mass-Spring system

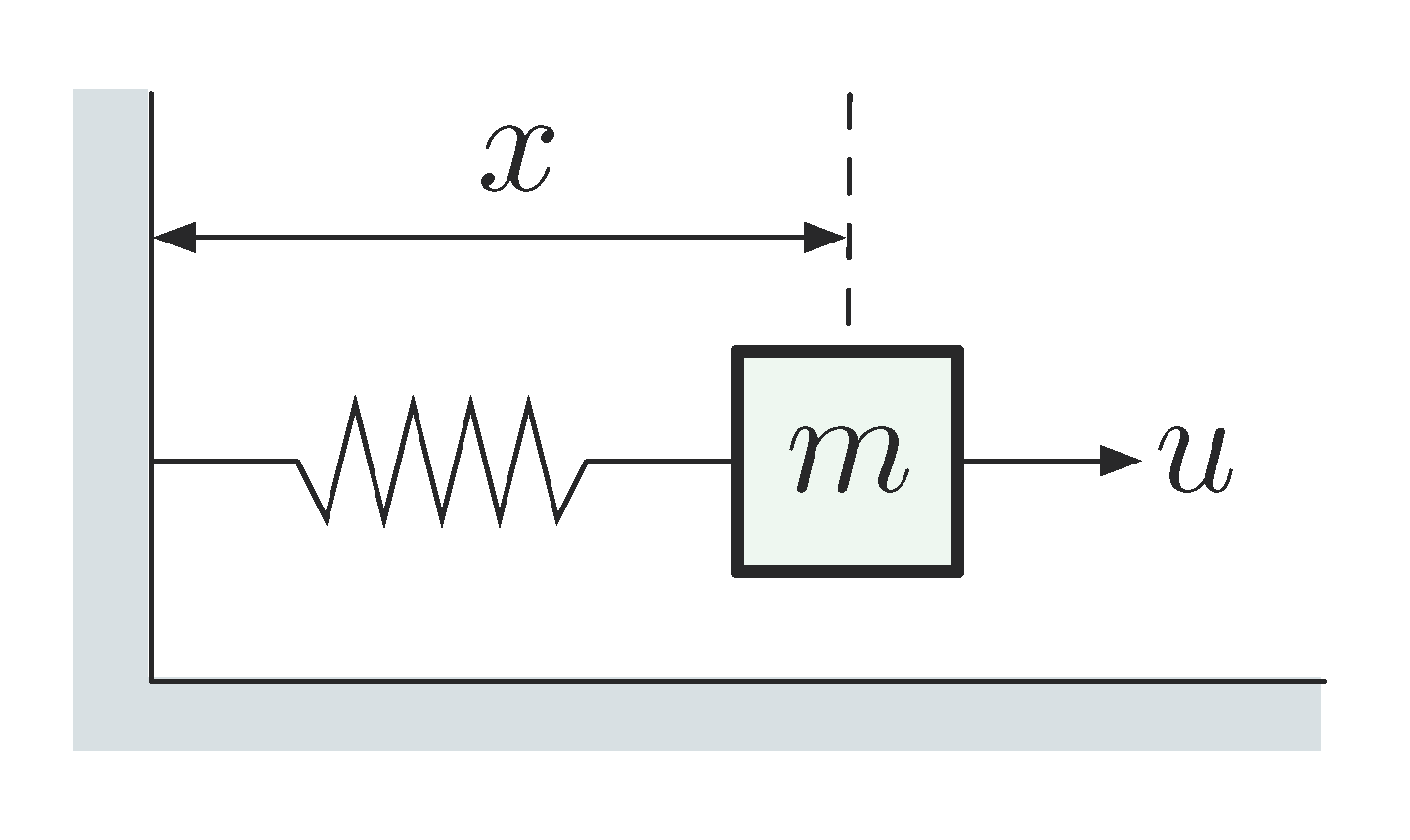
Figure 1: Example 1 – Mass-Spring system

Solution: By Newton’s second law, total force equals mass times acceleration. Therefore in this case,

$\begin{align*} \underbrace{F}_{\text{total force}} &= ma \\ &=\text{spring force} + \text{friction} + \text{external force}, \end{align*}$

where

$\begin{align*} \mbox{spring force } &= -kx \quad \mbox{(by Hooke's law)} \\ \mbox{friction force } &= -\rho\dot{x} \quad \mbox{(by Stokes' law, linear drag pegged to velocity)}, \end{align*}$

i.e., we have the governing equation

$\begin{align*} { -kx - \rho \dot{x} + u = m\ddot{x} }. \end{align*}$

We can move $x$ , $\dot{x}$ , $\ddot{x}$ to one side, leaving $u$ on the other, and normalize the leading coefficient,

$\begin{align*} \ddot{x} + \frac{\rho}{m}\dot{x} + \frac{k}{m}x = \frac{u}{m}. \end{align*}$

This gives us a second order linear ODE.

To rewrite it in canonical form, we convert it to a system of first order ODEs by introducing veloctiy variable $v = \dot{x}$ ,

$\begin{align} \label{d2_eq1} \left\{ \begin{array}{ll} \dot{x} = v \hspace{5cm} \text{(by definition of velocity)} \\ \dot{v} = - \frac{\rho}{m}v - \frac{k}{m}x + \frac{1}{m}u \end{array} \right. . \end{align}$

Equation $\eqref{d2_eq1}$ can also be written as (in order to see the matrix form more easily)

$\begin{align*} \left\{ \begin{array}{lrrrrr} \dot{x} =& (0)x &+ &(1) v &+& (0) u \\ \dot{v} =& (- \frac{k}{m})x &+ &(- \frac{\rho}{m})v &+& (\frac{1}{m})u \end{array} \right. . \end{align*}$

Finally, we can express it in matrix form,

$\begin{align*} \left(\begin{matrix} \dot{x} \\ \dot{v} \end{matrix}\right) &= \left( \begin{matrix} 0 & 1 \\ -\frac{k}{m} & -\frac{\rho}{m} \end{matrix}\right) \left(\begin{matrix} x \\ v\end{matrix}\right) + \left(\begin{matrix} 0 \\ \frac{1}{m} \end{matrix}\right)u. \end{align*}$

Example 2: Consider RL circuit as in Figure 2. Derive the governing differential equation and rewrite it in matrix form by reducing a higher order ODE to a set of first order ones.

RL circuit

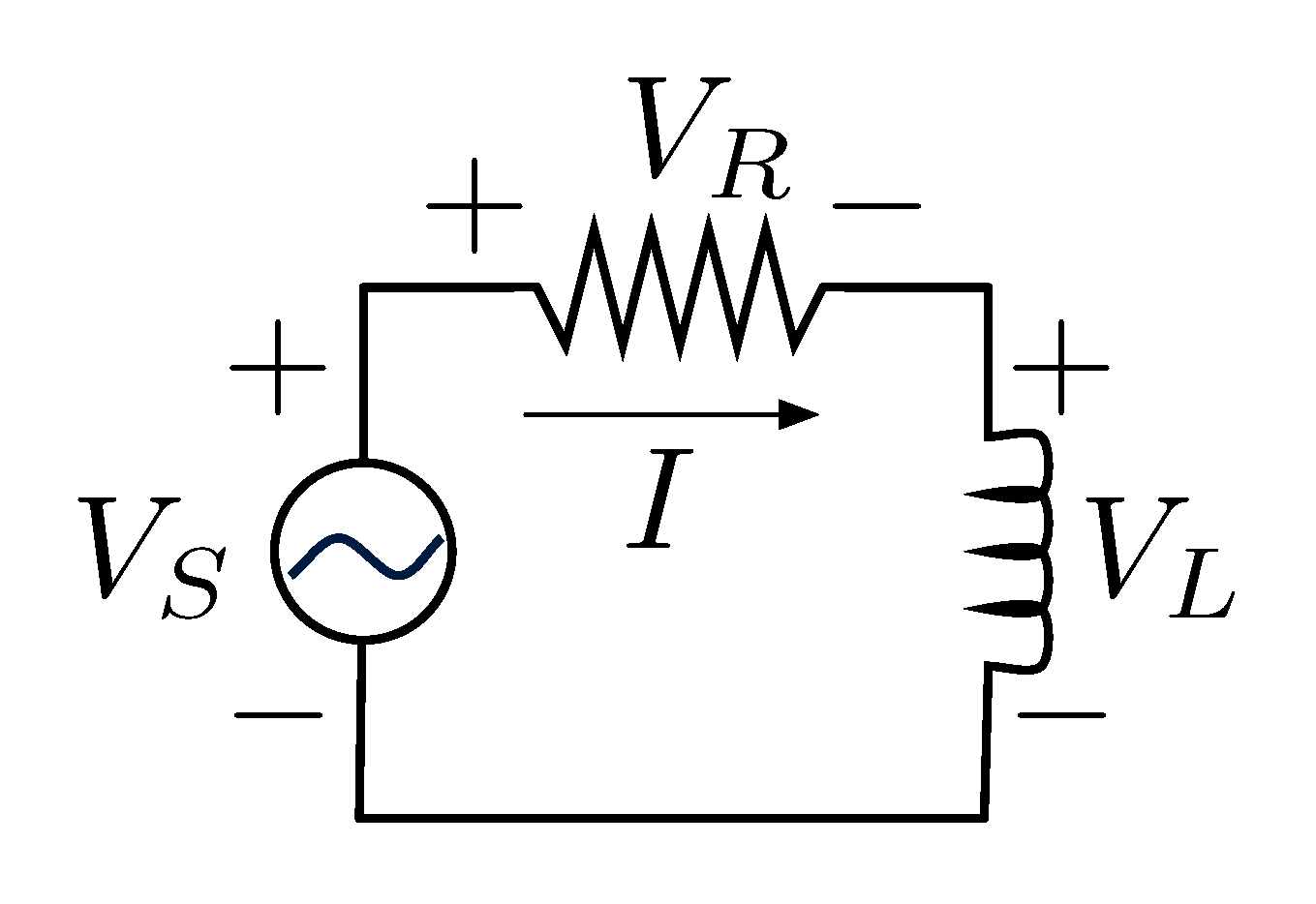
Figure 2: Example 2 – RL circuit

Solution: We can largely repeat what we did in Example 1 but instead apply Kirchhoff’s voltage law, total voltage drop along the circuit loop is $0$ .

$\begin{array}{rll} - V_S + V_R + V_L &=\, 0, & \text{(by Kirchhoff's voltage law)} \\ V_R &= \,RI, & \text{(by Ohm's law)} \\ V_L &= \,L\dot{I}. &\text{(by Faraday's law)} \end{array}$

Therefore, we have ${-V_S + RI + L\dot{I} = 0}$ .

$\begin{align*} \dot{I} = -\frac{R}{L}I + \frac{1}{L}V_S. \end{align*}$

Note this is a first order system.

General $n$ -Dimensional State-Space Model

If we apply abstraction to both Example 1 and Example 2 above, for a system with $n$ states and $m$ inputs,

$\begin{align*} \text{state } x = \left( \begin{matrix} x_1 \\ \vdots \\ x_n \end{matrix}\right) \in \RR^n, \qquad \text{input } u = \left( \begin{matrix} u_1 \\ \vdots \\ u_m \end{matrix}\right) \in \RR^m, \end{align*}$

a linear state space representation is a set of ODEs in matrix form

$\begin{align*} \left( \begin{matrix} \dot{x}_1 \\ \vdots \\ \dot{x}_n \end{matrix}\right) = \left( \begin{matrix} {\Huge A} \\ \\ {\text{$n \times n$}\atop\text{matrix}}\end{matrix}\right) \left(\begin{matrix} x_1 \\ \vdots \\ x_n \end{matrix}\right) + \left( \begin{matrix} {\Huge B} \\ \\ {\text{$n \times m$}\atop\text{matrix}}\end{matrix}\right) \left(\begin{matrix} u_1 \\ \vdots \\ u_m \end{matrix}\right). \end{align*}$

Or for short,

$\dot{x} = A_{n\times n}x + B_{n \times m}u.$

This is called the dynamics equation of the state-space representation. Sometimes we can augment this dynamics equation with output equation. Denote the $p$ outputs as a vector $y$ ,

$\begin{align*} \text{output } y &= \left( \begin{matrix} y_1 \\ \vdots \\ y_p \end{matrix}\right) \in \RR^p, \qquad y = Cx, \end{align*}$

where $C$ is a $p \times n$ matrix. For example, if we only care about (or can only measure) $x_1$ , then

$\begin{align*} y = x_1 = \left( \begin{matrix} 1 & 0 & \ldots & 0 \end{matrix} \right)\left( \begin{matrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{matrix}\right). \end{align*}$

The state-space representation of a system can be written as

$\begin{align*}\dot{x} &= Ax + Bu,\\ y &= Cx. \end{align*}$

State-space models are useful and convenient for writing down system models for different types of systems, in a unified manner.

We will use the classic example of a simple pendulum to illustrate how to work with state-space models.

Example 3: Consider the simple pendulum as in Figure 3. Derive the governing differential equation and write it in the state-space representation.

Simple pendulum

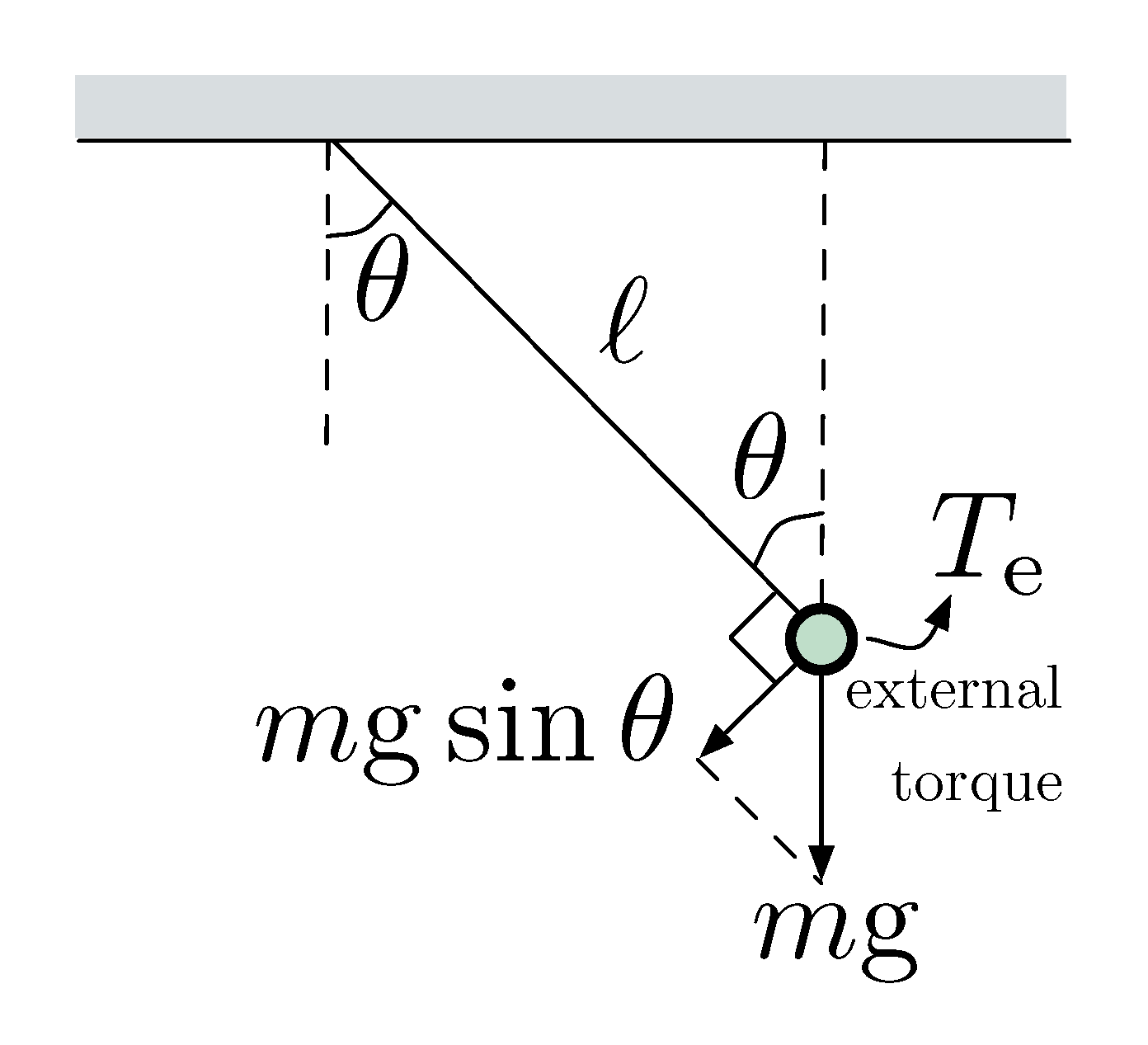
Figure 3: Example 3 – Simple pendulum

Solution: Similar to Example 1, we apply here Newton’s second law but in its rotational version. It says total torque equals moment of inertia times angular acceleration.

$\begin{align*} T &= J \alpha \\ \text{(pendulum torque } + \text{ external torque} &= \text{inertia} \times \text{angular acceleration),} \end{align*}$

where

$\begin{align*} \text{pendulum torque} &= \underbrace{-m {\rm g} \sin \theta}_{\text{force}} \times \underbrace{\ell}_{\text{lever arm}},\\ \text{moment of inertia } J &= m\ell^2. \end{align*}$

By substitution,

$\begin{align} \label{d2_eq2} \ddot{\theta} &= - \frac{{\rm g}}{\ell}\sin \theta + \frac{1}{m\ell^2}T_{\rm e}. \end{align}$

It is a nonlinear equation though. Recall for small $\theta$ , use the approximation $\sin \theta \approx \theta$ in Equation $\eqref{d2_eq2}$ ,

sinxx

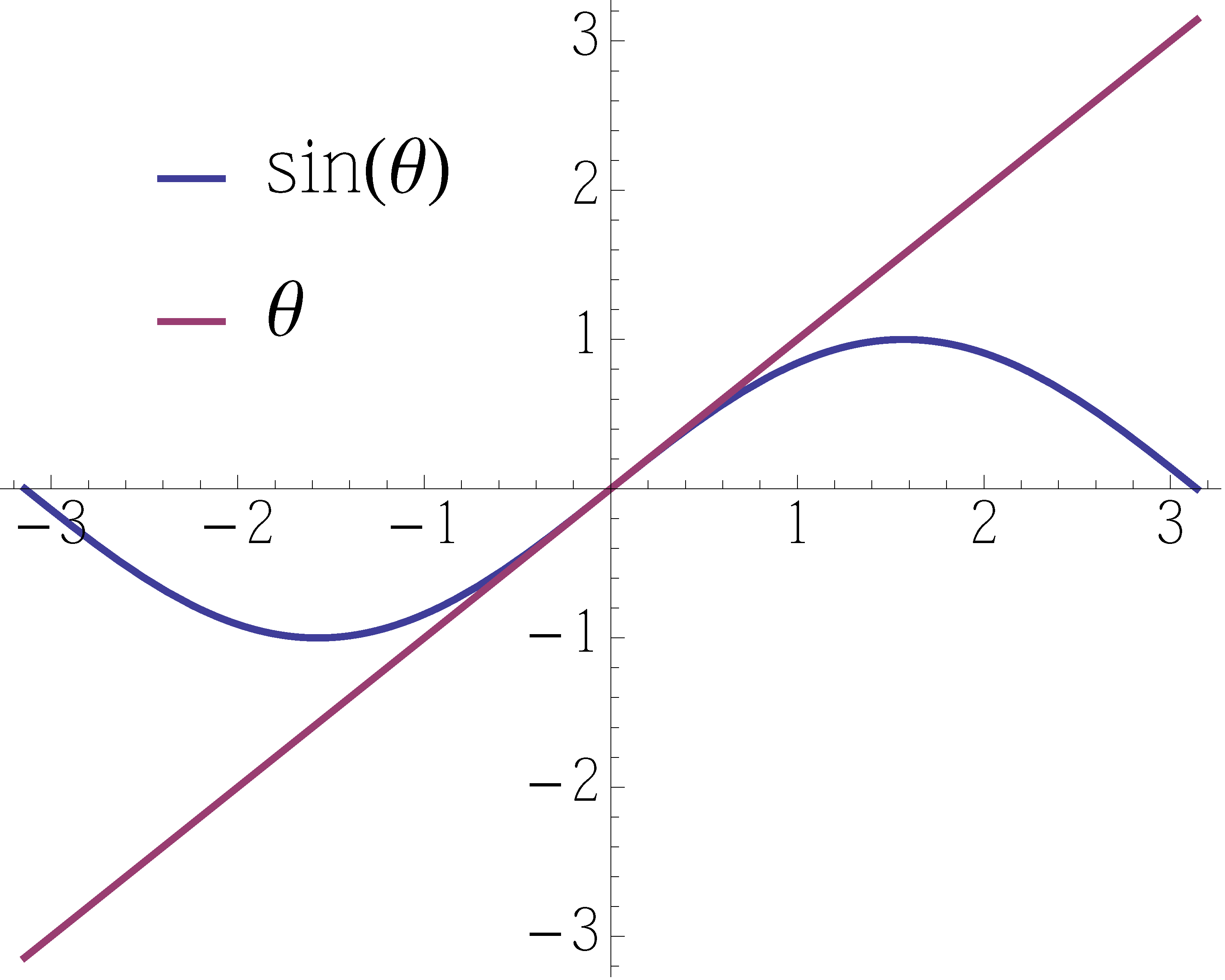
Overlaid $\sin x$ and $x$

We get

$\begin{align} \label{d2_eq3} \ddot{\theta} &= - \frac{{\rm g}}{\ell} \theta + \frac{1}{m\ell^2}T_{\rm e}. \end{align}$

Repeat what we did at the end of Example 1 to rewrite Equation $\eqref{d2_eq3}$ in state-space form: we introduce $\theta_1 = \theta,\,\, \theta_2 = \dot{\theta}$ , then

$\begin{align*} \dot{\theta}_2 &= - \frac{{\rm g}}{\ell} \theta + \frac{1}{m\ell^2} T_{\rm e} \\ &= -\frac{{\rm g}}{\ell}\theta_1 + \frac{1}{m\ell^2}T_{\rm e}. \end{align*}$

So the state-space representation of a simple pendulum is

$\begin{align*} \left( \begin{matrix} \dot{\theta}_1 \\ \dot{\theta}_2 \end{matrix} \right) = \left( \begin{matrix} 0 & 1 \\ -\frac{{\rm g}}{\ell} & 0 \end{matrix} \right) \left( \begin{matrix} {\theta}_1 \\ {\theta}_2 \end{matrix} \right) + \left( \begin{matrix} 0 \\ \frac{1}{m\ell^2} \end{matrix} \right)T_{\rm e}. \end{align*}$

Question: What if $\theta$ is not small? say, $\theta$ is around $\pi$ .

Answer: $\sin \theta \approx \pi - \theta$ if $\theta$ is around $\pi$ . (Why?)

Linearization of State-Space Models

Though in Example 3 we used the trick $\sin x \approx x$ around $x$ to obtain the linear state-space model, we are wondering if there is a general strategy to linearize state-space model. The answer is using Taylor series. Recall Taylor series expansion in one variable,

$\begin{align*} f(x) &= f(x_0) + f'(x_0)(x-x_0) + \frac{1}{2}f''(x_0)(x-x_0)^2 + \ldots \\ &\approx f(x_0) + f'(x_0)(x-x_0). \hspace{2cm} \text{(linear approximation around $x=x_0$)} \end{align*}$

For a general nonlinear control system

$\begin{align*} & \dot{x} = f(x,u) &\text{(nonlinear state-space model)} \\ & x = \left( \begin{matrix} x_1 \\ \vdots \\ x_n\end{matrix}\right), \quad u = \left( \begin{matrix} u_1 \\ \vdots \\ u_m \end{matrix}\right), \quad f = \left( \begin{matrix} f_1 \\ \vdots \\ f_n \end{matrix}\right), \end{align*}$

we can apply Taylor expansion in multivariables. Assume $x=0$ , $u=0$ is an equilibrium point: $f(0,0) = 0$ , i.e., when the system is at rest and no control is applied, the system does not move. Around $(x,u)=(0,0)$ , for each $f_i(x, u)$ of $f(x,u)$ , $i=1,\ldots,n$ ,

$\begin{align*} f_i(x,u) = \underbrace{f_i(0,0)}_{=0} &+ \frac{\partial f_i}{\partial x_1}(0,0)x_1 + \ldots + \frac{\partial f_i}{\partial x_n}(0,0) x_n \\ &+ \frac{\partial f_i}{\partial u_1}(0,0)u_1 + \ldots + \frac{\partial f_i}{\partial u_m}(0,0) u_m. \end{align*}$

After we assemble those $n$ equations, we get the linearized state-space model

$\dot{x} = Ax + Bu, \text{ where $A_{ij} = \frac{\partial f_i}{\partial x_j} \Bigg|_{x=0 \atop u=0},\,\, B_{ik} = \frac{\partial f_i}{\partial u_k} \Bigg|_{x=0 \atop u=0}$}.$ $A$ is nothing but the Jacobian of $f(x,u)$ w.r.t. $x$ at equilibrium and similarly $B$ is the Jacobian of $f(x,u)$ w.r.t. $u$ at equilibrium.

Important: Since we have ignored the higher-order terms, this linear system is only an approximation that holds only for small deviations from equilibrium.

Let’s use the general strategy instead of a trick to relinearize the nonlinear dynamics of a simple pendulum in Example 3.

Example 3 (revisted): Relinearize the state-space model of a simple pendulum in Example 3 above.

Solution: The original nonlinear state-space model:

$\begin{align*} \dot{\theta}_1 &= f_1(\theta_1,\theta_2,T_{\rm e}) = \theta_2, \hspace{5cm} \text{(already linear)}\\ \dot{\theta}_2 &= f_2(\theta_1,\theta_2,T_{\rm e}) = -\frac{{\rm g}}{\ell} \sin \theta_1 + \frac{1}{m\ell^2} T_{\rm e}. \end{align*}$

Linearize $f_2$ around equilibrium $(\theta_1,\theta_2,T_{\rm e}) = (0,0,0)$ :

$\begin{array}{rlrlrl} \frac{\partial f_2}{\partial \theta_1} &=\, - \frac{{\rm g}}{\ell} \cos \theta_1, & \frac{\partial f_2}{\partial \theta_2} &=\, 0, \qquad \frac{\partial f_2}{\partial T_{\rm e}} &\,= \frac{1}{m\ell^2}, \\ \frac{\partial f_2}{\partial \theta_1}\Bigg|_0 &=\, - \frac{{\rm g}}{\ell}, & \frac{\partial f_2}{\partial \theta_2}\Bigg|_0 &\,= 0, \qquad \frac{\partial f_2}{\partial T_{\rm e}}\Bigg|_0 &=\, \frac{1}{m\ell^2}. \end{array}$

Therefore the linearized state-space model of the pendulum is

$\begin{align*} \dot{\theta}_1 &= \theta_2,\\ \dot{\theta}_2 &= - \frac{{\rm g}}{\ell} \theta_1 + \frac{1}{m\ell^2}T_{\rm e}, \end{align*}$

which is the same as Example 3.

General Linearization Procedure

Note that if systems have different equilibria other than $(x, u) = (0,0)$ , we may apply translation to shift nonzero equilibrium to the origin:

$\begin{align*} &\underline{x} = x-x_0, \qquad \underline{u} = u - u_0, \\ &\underline{f}(\underline{x},\underline{u}) = f(\underline{x} + x_0, \underline{u} + u_0) = f(x,u). \end{align*}$

Since $\dot{\underline{x}} = \underline{f}(\underline{x},\underline{u})$ is a system with origin as its equilibrium, we can apply the aforementioned linearization method we discussed for such systems. After we compute Jacobians and formulate the linearization in terms of $\underline{x}$ and $\underline{u}$ , we substitute $\underline{x} = x-x_0$ , $\underline{u} = u - u_0$ to get a linearized model in terms of $x$ and $u$ .

Observation: For any linear system, it must have an equilibrium point at $(x,u) = (0,0)$ since if $f$ is already linear

$\begin{align*} f(x,u) = Ax + Bu \xrightarrow{x = 0,~u = 0} f(0,0) = A0 + B0 = 0. \end{align*}$

Prev	Top	Next
	ECE 486 Handbook

ECE 486 Control Systems Lecture 2

State-Space Representation of a System

State-Space Model – a Unified Framework

General nn-Dimensional State-Space Model

Linearization of State-Space Models

General Linearization Procedure

ECE 486 Control Systems
Lecture 2

General $n$ -Dimensional State-Space Model