Lattice Monte Carlo: Ising Model
Jump to 2-D Monte Carlo Simulation
The
Lenz-Ising Hamiltonian
The
Ising Model is the "fruit fly" of the study of phase transitions.
The notes on potentials , such as Jij,
discussed the generic points associated with performing lattice type Monte Carlo,
in particular how potentials might be obtained for a variety of different problems
that can be simulated via a lattice model. The basic Hamiltonian, or Energy functional,
required is
H({sl})=
-  ij Jij
sisj -
i
ij Jij
sisj -
i i hisi. (1)
where
we assume that the term i=j is ignored. Here, we shall only talk
about the Lenz (1920) or Ising (1925) type model (rather than a vector-type,
or Heisenburg, model) in which si are the thermodynamic "spin
variables" which can take the values ±1. Here, J can be (Ferromagentic)
FM-like interactions tending to cluster like spins together, or (Anti-ferromagnetic)
AFM tending to order spins periodically (e.g., ...up...dn...up...dn). (Ising
only studied this model in 1-D, where there is no phase transition.) For
generality, I have included an external magnetic field (in fact, I have
made it site dependent which for mathematical convienience allows one to
take derivatives with respect to field, useful for getting susceptibilities).
i hisi. (1)
where
we assume that the term i=j is ignored. Here, we shall only talk
about the Lenz (1920) or Ising (1925) type model (rather than a vector-type,
or Heisenburg, model) in which si are the thermodynamic "spin
variables" which can take the values ±1. Here, J can be (Ferromagentic)
FM-like interactions tending to cluster like spins together, or (Anti-ferromagnetic)
AFM tending to order spins periodically (e.g., ...up...dn...up...dn). (Ising
only studied this model in 1-D, where there is no phase transition.) For
generality, I have included an external magnetic field (in fact, I have
made it site dependent which for mathematical convienience allows one to
take derivatives with respect to field, useful for getting susceptibilities).
The
Ensemble Average
Within
any simulation the goal is to calculate some average of interest (which
varies with model). Thus, for quantity A, the
Ensemble Average over G states
<
A > NVT =  G A(G) e-H(G)/kBT
(2)
G A(G) e-H(G)/kBT
(2)
Probability Distribution (Ensemble Dependent)
p(G)
= e-H(G)/kBT/Z(N,V,T)
(3)
Partition Function
Z=
 G e-H(G)/kBT
(4)
G e-H(G)/kBT
(4)
The Metropolis Algorithm
The
Metropolis et al. (1954) came up with an efficient means of sampling the
required distribution function. The method works because of its relation
to a Markov Chain (random walk). A Markov Chain requires:
-
The
outcome of each trial belongs to a finite set of outcomes, {G1,
....,Gm, Gn....}.
-
The
outcome of each trial depends only on the outcome of the trial immediately
proceeding it.
Thus,
Gm and Gn are linked by some transition probability,
PImn. Here
 n
PImn=1, so that there is SOME OUTCOME.
n
PImn=1, so that there is SOME OUTCOME.
Repeated
application of PI with a starting probability pm can generate
all sequences in the Markov chain, i.e.,
 m pmPImn=pn,
m pmPImn=pn,
 n pnPInq=pq,
and so on.
n pnPInq=pq,
and so on.
Thus,
if you know pm and PImn you have everything to solve
problem. Unfortunately, you usually do not know pm and rarely
known anything about PImn. Within the Metropolis approach,
PImn
= Tmn ( 1 )
pn > pm m.ne.n
PImn
= Tmn (pn/pm)
pn < pm m.ne.n
Here,
Tmn (the 'a priori' probability) is a symmetric stochastic matrix
which determines entirely the properties of the Markov Process. The symmetric
property is not required, but using it establishes microscopic reversibility
of the probabilities in the simulation. Furthermore, it is straightforward
to show that PImm, the probability to stay in same state, is
always finite. The possibility to stay in same state is required to model
Markov process.
Metropolis
et al. chose to evaluate < A >NVT = < A >MC run
using an criteria which accepts (or rejects) a "Monte Carlo move" according
to the required statistical weight. More physically, it accepts an energy
lowering move with probability 1, so you always move "downhill" towards
a minima. However, it accepts an "uphill" move randomly if a random number
between (0,1) is less than pn/pm= e-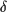 Emn/kBT. In other words p= min( 1, e-
Emn/kBT. In other words p= min( 1, e-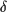 Emn/kBT ). This allows the system to explore
other minima rather than just local ones.
Emn/kBT ). This allows the system to explore
other minima rather than just local ones.
Notice
this ratio pn/pm does not depend on the partition
function, which is unknown. Furthermore, the ratio requires only determination
of 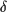 Emn rather than the entire configuration.
When considering long-range interactions, these usually cancel out and
never have to be considered, and, hence, the Metropolis method is computationally
efficient because it is the calculation of potential that is the time consuming
part.
Emn rather than the entire configuration.
When considering long-range interactions, these usually cancel out and
never have to be considered, and, hence, the Metropolis method is computationally
efficient because it is the calculation of potential that is the time consuming
part.
Nearest-Neighbor
Model and Simulation of Averages
The
so-called Nearest-Neighbor Ising model is one in which Jij
= J if i and j are nearest neighbors, and 0 otherwise.
Even for this very simple interaction the statistical mechanics and phase
transformation can be very interesting depending on the type of Bravais
lattice and dimensionality of lattice. In other words, you do not need
complexity of potential to get complex phase behavior.
For
the Nearest-Neighbor Ising Model, the interesting thermal averages are
the Energy, E, and the Magnetization, M, and perhaps also the pair correlations
(or susceptibility). The site Magnetization, Mi, is < si
>. Hence, using Eqs. 1-4, you can show that
Mi
= < si > = < tanh B( j Jij sj + hj) >
where
the thermal average <...> is over the remaining spin variables not on
site i. Let us explore a Mean-Field Theory approximation to this
where where the average has been moved through the TANH function, or equivalently,
we have ignored correlations in the variables, or, in other words, rather
than handle si sj we suppose that site i
"feels" the average effect of all other sites, so si < sj
>. In this approximation the statistical averages can be performed because
correlations between specific sites have been ignored. In any case,
Mi
= < si > = tanh B(
j Jij sj + hj) >
where
the thermal average <...> is over the remaining spin variables not on
site i. Let us explore a Mean-Field Theory approximation to this
where where the average has been moved through the TANH function, or equivalently,
we have ignored correlations in the variables, or, in other words, rather
than handle si sj we suppose that site i
"feels" the average effect of all other sites, so si < sj
>. In this approximation the statistical averages can be performed because
correlations between specific sites have been ignored. In any case,
Mi
= < si > = tanh B( j Jij < sj > + hj) .
This
is a transcendental equation whose solution may be found graphically. The
R.H.S. TANH function is a slanted s-like curve and the L.H.S. is a straight
line. Their intersection is a solution. We find two types. For temperatures
above a certain TCritical, the solution is at M=0, whereas at
some lower T there are two solution ±M. These two solutions are
the two possible ground states of the Ising model: all +1 spins, or all
-1 spins (both have same E). We find that there is then a phase transition
that can occur, i.e. a TCritical where above M=0 and below M
is finite.
j Jij < sj > + hj) .
This
is a transcendental equation whose solution may be found graphically. The
R.H.S. TANH function is a slanted s-like curve and the L.H.S. is a straight
line. Their intersection is a solution. We find two types. For temperatures
above a certain TCritical, the solution is at M=0, whereas at
some lower T there are two solution ±M. These two solutions are
the two possible ground states of the Ising model: all +1 spins, or all
-1 spins (both have same E). We find that there is then a phase transition
that can occur, i.e. a TCritical where above M=0 and below M
is finite.
-
In
1-D, however, there is no phase transition. The fully-correlated state
with all spins up can be easily destroyed by just moving one spin down.
Hence only at T=0 K, are all spins aligned.
-
In
2-D, there is finite phase transition, along with usual latent heat, etc.
This has been solved exactly by Onsager, but only for h=0. The critical
behavior also depends on type of lattice. On a square lattice with n.n.
only, the spins align when (kBT)-1 > 0.4407/J, in
zero field.
-
In
3-D there is no analytic solution, and it may be impossible to do so. Hence
the importance of simulation.
-
Above
TCritical, there is short-range order arising from the correlations
that form, and indicated by the pair correlations. Below TCritical,
there is long-range order that forms due to these correlations becoming
infinite ranged, indicated by the appropriate order parameter, which is
M for the Ising model.
So
based on intuition from MFT, we at least can expect some interesting critical
behavior associated with the numerical investigation of the Ising Model.
Explore
the 2-D Lattice Monte Carlo
with N.N. Ising Model using a JAVA Applet.
Relation
to Physical Systems
The
Ising model appears to be a simple model of little relevance to most physical
problems. The closest physical problem is a magnetic phase transformation
for a simple ferromagnet. However, it is a good model also for:
-
Liquid-Vapor
transformation, where clustering of si= 1 represents condensation
of the gas molecules due to their attractive intereaction. As gas molecules
interact and no longer behave as non-interacting gas (i.e., PV=nRT), then
there can be transition to liquid phase.
-
Liquid
Mixtures. "Critical opalescence" arises from the short-range correlation
of disordered (mixed) phase and there is scattering of light (sample is
opaque) and below transition there is long-range correlation in the single
phase mixture and sample is transparent because light does not scatter.
-
An
Alloy, if one considers up=A atoms and down=B atoms. In this case, we have
a binary alloy and the magnetic field, h, is the chemical potential (for
h=0, we have 50-50 alloy). Nonetheless, non-zero field (finite chemical
potential difference) is important generally. The solution of this finite-field
problem is not even known in 2-D. Hence, numerical simulations are required.
-
Liquid
Crystal and Polymers in some instances can also be modeled via lattices.
For example, molecules that rotate (as with polarization of liquid crystals)
but more-or-less form on a lattice are treated this way.
TOP
October 9 1998 by D.D. Johnson
(updated
Oct 28, 1999)
Calendar
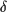 Emn/kBT. In other words p= min( 1, e-
Emn/kBT. In other words p= min( 1, e-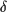 Emn/kBT ). This allows the system to explore
other minima rather than just local ones.
Emn/kBT ). This allows the system to explore
other minima rather than just local ones.
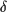 Emn rather than the entire configuration.
When considering long-range interactions, these usually cancel out and
never have to be considered, and, hence, the Metropolis method is computationally
efficient because it is the calculation of potential that is the time consuming
part.
Emn rather than the entire configuration.
When considering long-range interactions, these usually cancel out and
never have to be considered, and, hence, the Metropolis method is computationally
efficient because it is the calculation of potential that is the time consuming
part.