CS440/ECE448 Spring 2022
Assignment 3: Search

i. Introduction

Key terms:

In this assignment, we will implement general-purpose search algorithms and use them to solve pacman-like maze puzzles. This assignment has four parts (last part is extra credit).

  1. Breadth-first search, with one waypoint.
  2. A* search, with one waypoint.
  3. A* search, with many waypoints.
  4. Heuristic search, with many waypoints.

Throughout this assignment, the goal will be to find a path from a given starting position in a maze which passes through a given set of waypoints elsewhere in the maze. We will begin by finding a path from the starting position to a single destination waypoint. Then we will generalize the implementation to handle multiple waypoints. Finally, we will explore heuristics to handle large numbers of waypoints in a reasonable amount of time.

ii. Environment

Key terms:

This assignment is written in Python 3. If you have never used Python before, a good place to start is the Python tutorial. We recommend using Python version 3.8 or later.

This assignment contains visualization tools which depend on pygame. You can install pygame locally using the pip3 tool.

iii. Getting Started

Key terms:

To get started on this assignment, download the template code. The template contains the following files and directories:

The data/ directory contains the maze files we will be using in this assignment.

The main.py file will be the primary entry point for this assignment. Let’s start by running it as follows: 

python3 main.py --human data/part-1/small

This will open a pygame-based interactive visualization of the data/part-1/small maze.

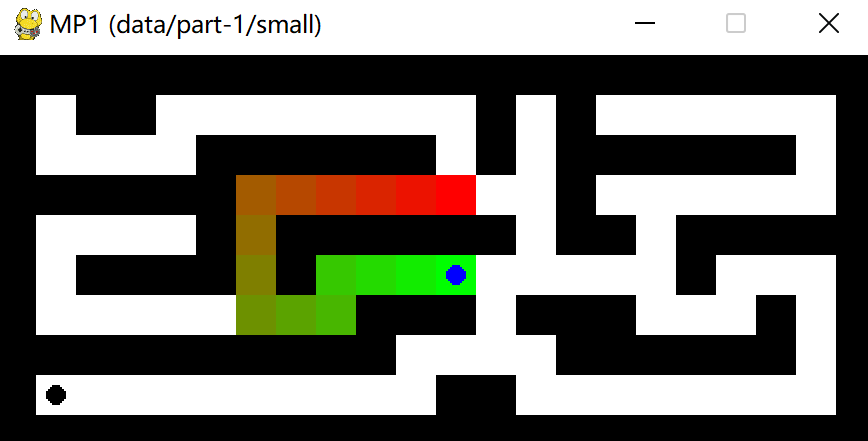
pygame visualization

The blue dot represents the agent. You can move the agent, using the arrow keys, to trace out a path, shown in color.

note: if the red-green gradient is hard for you to see, you can make the visualization use an alternative color scheme by specifying the --altcolor option.

The black dots represent the maze waypoints. Observe that this maze contains a single waypoint, in the lower left-hand corner. When you implement the search algorithms for this assignment, you will need to compute a path that takes the agent through all of the waypoints in the maze.

We will grade your submissions using grade.py. This file is available to you, so that you can understand how this assignment will be graded.

Let's see what happens when we run this script:

./grade.py

running in student mode (instructor key unavailable)
{'visibility': 'visible',
 'tests': ({'name': "part-1: `validate_path(_:)` for 'tiny' maze",
            'score': 0.0,
            'max_score': 0.5,
            'visibility': 'visible'},
           {'name': "part-1: correct path length for 'tiny' maze",
            'score': 0.0,
            'max_score': 0.5,
            'visibility': 'visible'},
           {'name': "part-1: `validate_path(_:)` for 'small' maze",
            'score': 0.0,
            'max_score': 0.5,
            'visibility': 'visible'},
           {'name': "part-1: correct path length for 'small' maze",
            'score': 0.0,
            'max_score': 0.5,
            'visibility': 'visible'},
...

As you can see, we have a score of 0, since we have not implemented any of the functions in search.py. We will do this in the next few sections.

iv. The Maze API

It is helpful to understand some of the infrastructure we have provided in the starter code. All the important functions and variables you should use can be found in maze.py. The Maze class is the abstraction that converts the input ASCII mazes into something whose properties you can access straightforwardly.

You can inspect the ASCII maze cells programatically using the __getitem__(_:_:) subscript. 

cell = maze[row, column]

warning: this subscript uses matrix notation, meaning the first index is the row, not the column. Spatially, this means the y-coordinate comes before the x-coordinate.

In the rest of this guide, we will use i to refer to a row index, and j to refer to a column index.

The maze size is given by the size member. The size.x value specifies the number of columns in the maze, and the size.y value specifies the number of rows in the maze. 

rows    = maze.size.y
columns = maze.size.x

Keep in mind that the coordinate order in size is reversed with respect to the two-dimensional indexing scheme!

Each cell in the maze is represented by a single character of type str. There are four kinds of cells, which should be self-explanatory:

For obvious reasons, a maze will only ever contain one starting position, but it can contain an arbitrary number of waypoint cells. However, for Part 1, you can assume there is only one waypoint cell in the maze.

You can determine what kind of cell a particular maze cell is by using the maze legend, available in the legend property.

# `True` if the cell is a wall cell
cell == maze.legend.wall 

# `True` if the cell is the starting position
cell == maze.legend.start

# `True` if the cell contains a waypoint
cell == maze.legend.waypoint

You can assume that any cell that is not a wall, start position, or waypoint is empty.

The Maze type also supports the following interfaces, which may or may not be useful to you:

You will become very familiar with the Maze class as you implement the parts in the next sections. Remember, do not modify maze.py.

Key terms:

For Part 1 of this assignment, we will implement breadth-first search (BFS) for a single waypoint. Specifically, we will implement a function bfs(_:) in search.py with the following signature:

# search.py
def bfs(maze):

Your bfs(_:) implementation should return a maze path, which should be a sequence of (i, j) coordinates. The first vertex of the path should be start, and the last vertex should be waypoints[0].

hint: the deque type, available in the collections module, may be useful.

The diffculty in this question mostly arises from the choice of the state space. What information should we hold about the maze? Sure, the current position is useful, but is there anything else you should keep track of? Hint: in the future parts of the assignment, you will have to go through multiple waypoints, but as you will see, looping over the waypoints will not work. Handling this generalization now will save you from doing extra work in future parts.

You can view your generated path, and some interesting statistics about it, by running main.py as follows:

python3 main.py data/part-1/small --search bfs

You can test the other mazes by replacing the specified maze file small (in data/part-1/) with one of tiny, small, no_obs, or open.

python3 main.py data/part-1/tiny --search bfs
python3 main.py data/part-1/small --search bfs
python3 main.py data/part-1/no_obs --search bfs
python3 main.py data/part-1/open --search bfs

If you have implemented bfs(_:) correctly, you should see your score from grade.py increase to 50% for the Part 1 test cases. This is because we have not provided the full answer key containing the expected path vertices in key-student, for obvious reasons. However, if you upload your search.py file to Gradescope, the autograder will show you your complete score for Part 1.

2. A*

Key terms:

For Part 2 of this assignment, solve the same set of mazes as in the previous part, this time using the A* search algorithm.

Write your implementation as a function astar_single(_:) in search.py with the following signature: 

def astar_single(maze):

hint: the heapq module may be useful.

Since all the test mazes contain only a single waypoint, you can use the Manhattan Distance from the agent's current position to the singular waypoint as the A* heuristic function. For two grid coordinates a and b, the manhattan distance is given by:

abs(a[0] - b[0]) + abs(a[1] - b[1])

You can test your implementation by running main.py as follows, replacing data/part-2/small as needed: 

python3 main.py data/part-2/tiny --search astar_single

You should find that the path lengths returned by A* are the same as those computed by breadth-first search, but A* explores fewer states.

3. A* for Multiple Waypoints

Now, consider the more general and harder problem of finding the shortest path through a maze while hitting multiple waypoints. As suggested in Part 1, your state representation, goal test, and transition model should already be adapted to deal with this scenario. The next challenge is to solve different mazes using A* search with an appropriate admissible heuristic that takes into account the multiple waypoints.

In the past, one popular approach that has been taken is what we refer to as the "greedy" method, that is to greedily choose the closest waypoint to the current position, run A* on it, and repeat until all waypoints have been reached. Why is this suboptimal? Think about what happens if the nearest waypoint is in the center of a long line of waypoints. Clearly, this strategy will not always choose the best path.

Instead, there is a beautiful heuristic that will not only find the optimal path through all the waypoints, but is admissable as well. It is based on a data structure you hopefully have seen before: the Minimum Spanning Tree (MST). Instead of computing the distances to each waypoint from the current position, it would be more helpful to obtain an estimate of the cost of reaching the rest of the unreached waypoints once we have reached one. Obtaining this estimate can be done with an MST: by constructing a graph where the vertices are the waypoints and each edge connecting w_i to w_j has weight manhattan_distance(w_i, w_j) for all pairs of vertices (w_i, w_j), the MST represents the approximate lowest cost path that connects all the waypoints. Since it strictly underestimates the cost of going through all the waypoints, this is an admissable heuristic.

To help you, we have included a function MST(_:) in search.py that will generate an MST for you. It is up to you to utilize this to obtain the information you want, depending on how many waypoints remain. In addition, to make things faster, you can also cache/memoize values since many states would use the same value from the MST.

So, suppose you are in the middle of a search. You're at some location (x,y) with a set of S waypoints still to reach. Your heuristic function h should be the sum of the distance from (x,y) to the nearest waypoint, plus the MST length for the waypoints in S.

Write your implementation as a function astar_multiple(_:) in search.py with the following signature: 

def astar_multiple(maze):

You can test your implementation by running main.py as follows, replacing data/part-3/small as needed: 

python3 main.py data/part-3/tiny --search astar_multiple

4. Extra Credit: Suboptimal Heuristic Search for Many Waypoints

Sometimes, even with A* and a good heuristic, finding the optimal path through all the waypoints is hard. In these cases, we'd still like to find a reasonably good path, quickly. Write a suboptimal search algorithm that will do a good job on the maze with many waypoints. You are given a medium maze for local testing. Note that applying part 3 code to this maze will be very slow. Your algorithm could either be A* with a non-admissible heuristic, or something different altogether. To earn full credits, your function must solve both medium and large (hidden on gradescope) mazes in less than 6 minutes (when we test on gradescope). Assuming that it finishes in that amount of time, grading will be based on the length of your returned path and its validity.

Write your implementation as a function fast(_:) in search.py with the following signature: 

def fast(maze):

You can test your implementation by running main.py as follows: 

python3 main.py data/part-4/medium --search fast

Submitting to Gradescope

Submit this assignment by uploading search.py to Gradescope. You can upload other files with it, but only search.py will be retained by the autograder. We encourage you to submit to Gradescope early and often as you will be able to see your final score there. The local grade.py is purely for your convenience and does not include the full suite of tests you will be graded on.

This assignment is worth 100 points, plus 10 extra credits. The grading rubric is as follows:

part total points points per maze
1 30 points 5 points
2 25 points 5 points
3 45 points 5 points
Extra credit 10 points 5 points

Plagiarism

It's ok to copy small amounts of utility code from 3rd party sources, as long as the source is acknowledged. However, it is not ok to consult or copy from full implementations of the algorithm in question, e.g. old code from similar MPs (at UIUC or elsewhere). We will use a code similarity detection system. Please do not copy code from your classmates. Thanks!