Kirchhoff's Laws
Using KVL to find voltages across generic elements
Learn It!
Pre-Requisite Knowledge
To understand this section, you need to know the following concepts:
Goal
Using KVL
Use KVL to find the voltages across generic elements in a circuit
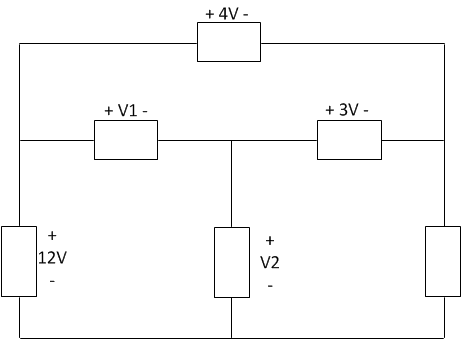
Find the values of V_1 and V_2 in the diagram at left.
\begin{equation} a. V_1 = 1 \text{ V} \text{ and } V_2 = 13 \text{ V} \\b. V_1 = 1 \text{ V} \text{ and } V_2 = 11 \text{ V} \\c. V_1 = 5 \text{ V} \text{ and } V_2 = 7 \text{ V} \\d. V_1 = 7 \text{ V} \text{ and } V_2 = 5 \text{ V} \\e. V_1 = 7 \text{ V} \text{ and } V_2 = 19 \text{ V} \end{equation}
\begin{equation} a. V_1 = 1 \text{ V} \text{ and } V_2 = 13 \text{ V} \\b. V_1 = 1 \text{ V} \text{ and } V_2 = 11 \text{ V} \\c. V_1 = 5 \text{ V} \text{ and } V_2 = 7 \text{ V} \\d. V_1 = 7 \text{ V} \text{ and } V_2 = 5 \text{ V} \\e. V_1 = 7 \text{ V} \text{ and } V_2 = 19 \text{ V} \end{equation}
+
?
What are these boxes?
Part 1
Find the first unknown voltage
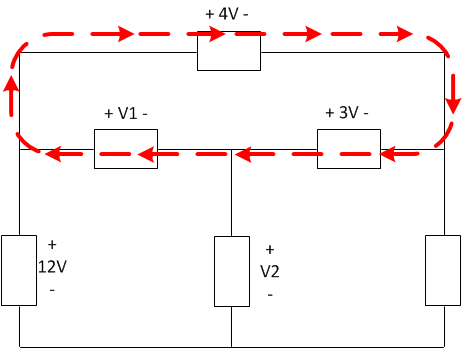
Let's pick a loop to analyze. We would prefer to use a loop that contains only one unknown. The left loop has both V_1 and V_2, but the top one contains only V_1.
+
⇨
Finding the signs
V_1 \quad 4 \quad 3 = 0
Now we apply KVL to find the (unknown) V_1. We know it will involve V_1, 4 and 3.
+V_1 \quad 4 \quad 3 = 0
Now we need to determine what sign each of the elements takes. Getting this wrong will mess up everything, so let's be careful. When traveling from the - terminal to the + terminal, we assign that a positive sign because it's a voltage rise. This means that V_1 will be positive.
+V_1 -4 +3 = 0
However, across the 4 V element we are traveling from the + terminal to the - terminal. That's a voltage drop, so we assign a negative sign. This means that 4 will be negative.
Across the 3 V element, we are traveling from the - terminal to the + terminal, another rise. So the 3 is positive.
Across the 3 V element, we are traveling from the - terminal to the + terminal, another rise. So the 3 is positive.
+V_1 -4 +3 = 0
Final KVL Equation
+
?
Reasoning behind this loop
We chose the loop to be going clockwise because that would make V_1 positive in our equation, which makes it more convenient to solve. We could have made it counterclockwise but that would have been a little more work.
+
!
Alternative loop
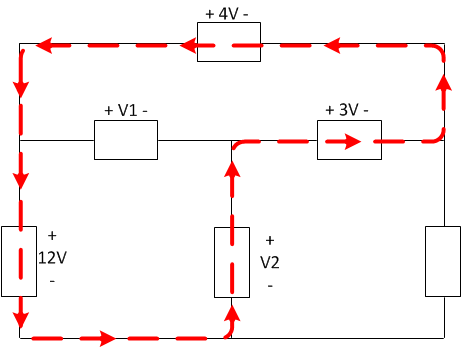
We could have chosen this loop and started by solving for V_2. But since this loop has 4 elements rather than 3, it would be more work. Extra loops can be an effective way to check your work, though, because you didn't use them to construct your answer
★
V_1 = 1
Combining terms and moving the constants to the right hand side gives us an answer.
+
?
What if we got a negative value?
Note that it is possible we could have obtained a negative value for V_1. That is fine because the polarity labels around voltage just indicate a reference polarity and don't mean that the polarity should be one way or the other.
Part 2
Finding the second unknown voltage

Now that we have V_1, we can find another loop that gives us V_2.
+V_2 + V_1 - 12 = 0
Now we use KVL again. The voltage across the 12 V element is a drop, so it appears as negative in our equation.
+
?
Why this loop?
We chose counter-clockwise this time, because we want V_2 to be positive in our final equation.
+
⇨
Solve KVL equation
V_2 = 12- V_1
Move everything except V_2 to the right hand side by subtraction.
Note that we kept V_1 as a variable. If we had made a mistake, having it in variable form makes it easier to fix when re-doing a problem.
Note that we kept V_1 as a variable. If we had made a mistake, having it in variable form makes it easier to fix when re-doing a problem.
V_2 = 12-1
Substitute V_1=1
V_2 = 11
Substitute V_1=1
★
V_1 = 1 \text{ V} \text{ and } V_2 = 11 \text{ V}
Choice b was the correct answer


