Equivalent Resistance
Use Series, Parallel, and Ohm's law to find Equivalent
Resistance
Learn It!
Pre-Requisite Knowledge
Goal
Find the equivalent resistance.
This group of resistors will
act like one equivalent resistor. What is its resistance?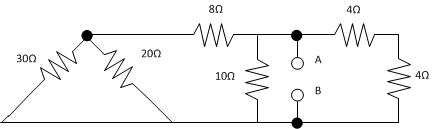
Part 1
Redraw The Circuit
+
1A
Circuit transformation
Circuit diagrams are an abstraction of
a real circuit, there are many ways to draw and redraw them. This example shows you how
to redraw circuit diagrams to suit out purposes
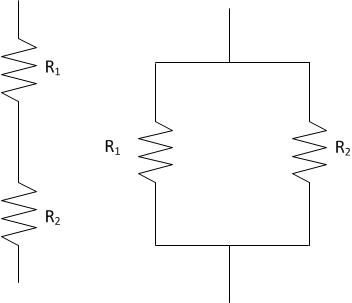
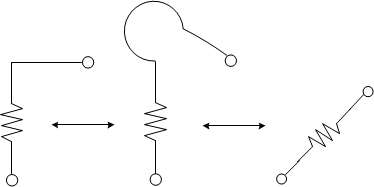
We want stuff that looks like this. Just trust me. All the
resistors are oriented vertically. Terminals exiting from the middle out of the top
and bottom.
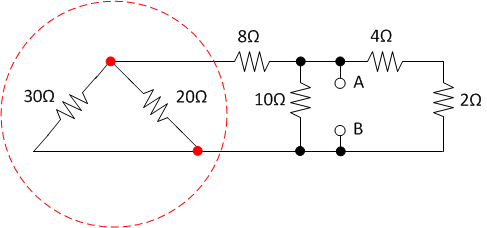
Ultimately we want only vertical resistors. Our first task
is try to resolve this diagonal part on the left side. We don't like
diagonals.
+
?
Stretch and bend
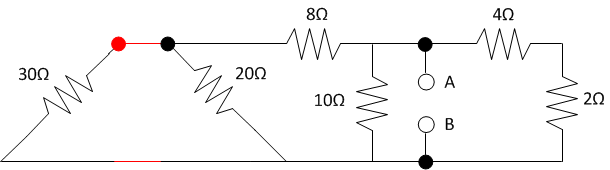
As our first move, we'll
stretch some wire to make that T junction a little nicer to look at.
+
?
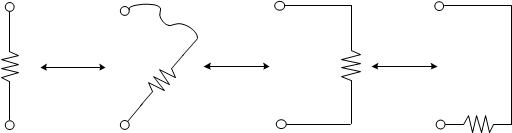
Rotate
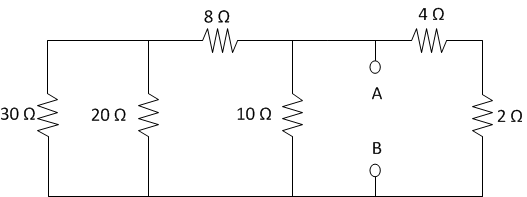
Let's
rotate them to get them vertical. We'll make them immediately recognizable
later, after we work on other parts of the circuit.
+
?
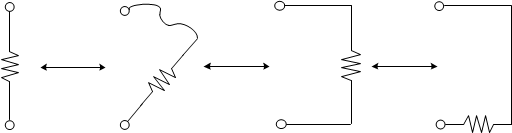
Slide
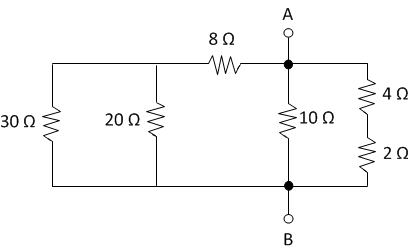
Now let's clean up the right side a bit. we can
slide the \(4 \Omega\) resistor around the corner, YAY!
We can also T-slide points A and B to coincide with the junction of the \(10 \Omega\) resistor
We can also T-slide points A and B to coincide with the junction of the \(10 \Omega\) resistor
+
?
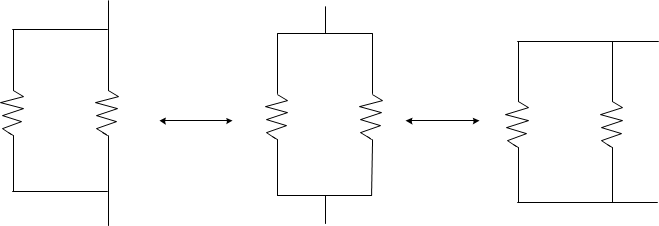
T-Slide
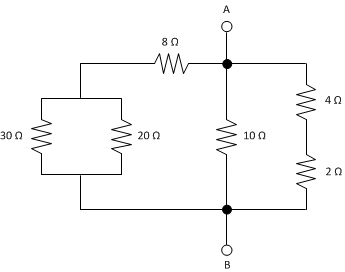
Now we want to work on getting that \(8 \Omega\) resistor
in line. First, let's do a
T-slide to move that corner to the center of the wire. This gives us
terminals poking out the top and bottom.
Now we slide resistor 8 along the wire around the corner onto the vertical segment.
Now we slide resistor 8 along the wire around the corner onto the vertical segment.
★
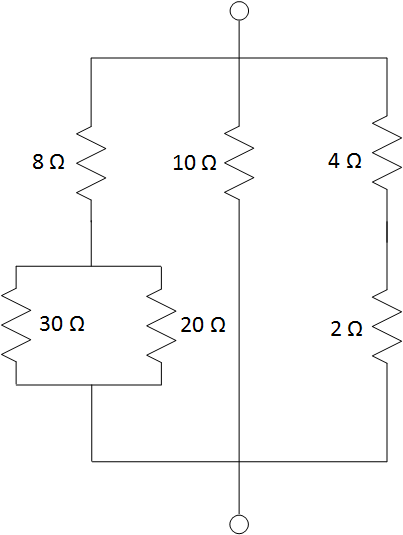
Now our circuit is nicely transformed. After doing this a few
times, you will be able to do all this in your head. It just takes a little
practice.
+
!
Are the legal moves 'real'
These "legal moves" are analogous to
operations on a breadboard, too. They are not just pure abstractions for
diagrams.
Part 2
Finding Equivalent Resistance
Use parallel and series formulas to decompose circuits one piece at a
time.
+
2A
Reduce two series resistors on the right

This circuit is nice. The circled segments look like those
special patterns mentioned earlier in the example.
These configurations are common and important enough to have names.
The one on the right is called Series
These configurations are common and important enough to have names.
The one on the right is called Series
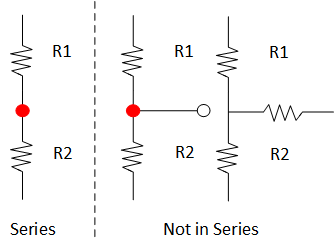
Two resistors are in series when they share a single node that no other
element is connected to.
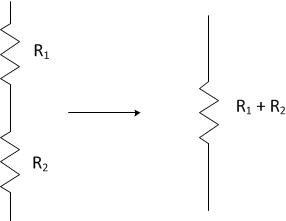
We can replace a series pattern of resistors with a single
resistor with the
Equivalent resistance denoted with the symbol \(R_{eq} \)
\(R_{eq} =R_1+R_2\)
\(R_{eq} =R_1+R_2\)
+
?
How to understand and remember this formula?
+
!
Proof
\[R_{eq1} = R_1 + R_2 = 4+2 = 6 \]
Now our circuit is nicely transformed. After doing this a few
times, you will be able to do all this in your head. It just takes a little
practice.
+
2B
Reduce two parallel resistors on the left
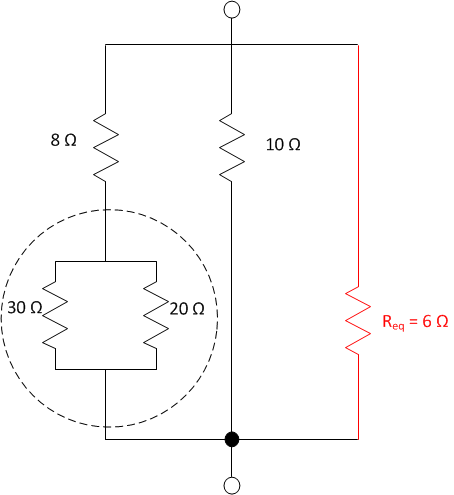
Redraw the diagram with the equivalent resistor.
The circled configuration is also a special configuration. it is called Parallel
The circled configuration is also a special configuration. it is called Parallel
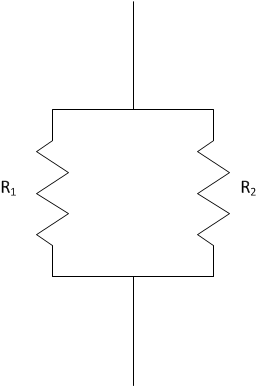
Resistors are in parallel if they share the same nodes but
go along different wires
It has an equivalent resistance of
\(R_{eq} = \dfrac{1} {\dfrac{1}{R_1} + \dfrac{1}{R_2}} \)
Another way of representing this is the Product over sum rule
\(R_{eq} = \dfrac {R_1 * R_2} {R_1 + R_2} \)
It has an equivalent resistance of
\(R_{eq} = \dfrac{1} {\dfrac{1}{R_1} + \dfrac{1}{R_2}} \)
Another way of representing this is the Product over sum rule
\(R_{eq} = \dfrac {R_1 * R_2} {R_1 + R_2} \)
+
?
How to understand and remember this formula?
Remember the
formula with resistivity? Putting two identical resistors in parallel is like
doubling the area of a piece of wire. This lowers resistance by providing a wider
path for the current.
+
!
Proof
\[R_{eq2} = \dfrac{1}{\dfrac{1}{R_1} + {\dfrac{1}{R_2}}} =
\dfrac {1} {\dfrac{1}{20} + \dfrac{1}{30}} = 12 \]
Apply the parallel resistance formula! Note that our answer is
reasonable: a parallel configuration reduces resistance.
+
2C
Reduce the series resistors on the left
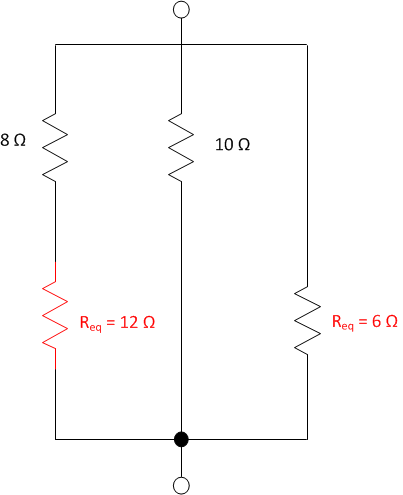
Redraw the diagram with the parallel resistors replaced
with their equivalent resistance.

Search for easy reductions. The \(8\Omega\) resistor and
Req (\(12\Omega\) together) are in
series.
\[R_{eq3} = 8 +12 = 20 \]
Apply the series equivalent resistance formula.
+
2D
Combine three parallel resistors
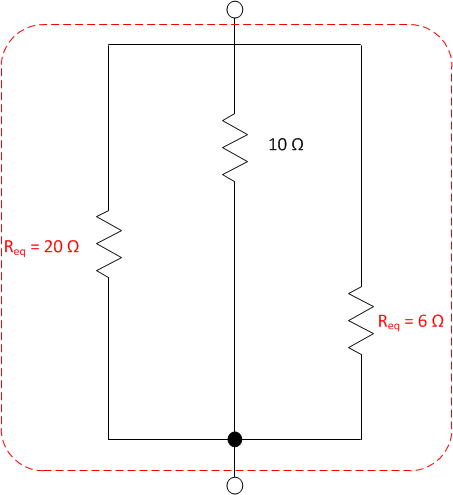
Let's redraw the diagram with the third reduction
inserted.
We're in the home stretch, After doing a few of these, you will be able to do more than one step at a time.
We're in the home stretch, After doing a few of these, you will be able to do more than one step at a time.

The parallel formula works for more than two resistors as
well. The three or four resistor version of the "product over sum" rule is ugly.
don't use it
In general...
For parallel combinations of resistors
\(R_{eq}=\dfrac{1}{\dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3} + \dfrac{1}{R_4} + ...}\)
In general...
For parallel combinations of resistors
\(R_{eq}=\dfrac{1}{\dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3} + \dfrac{1}{R_4} + ...}\)
\(R_{eq} = \dfrac{1}{\dfrac{1}{20} + \dfrac{1}{10} +
\dfrac{1}{6}} = 3.157 \Omega \)
★
\[R_{eq} = \dfrac{1}{\dfrac{1}{20} + \dfrac{1}{10} +
\dfrac{1}{6}} = 3.157 \Omega \]
Apply the parallel resistance formula to three resistors.
We have succeeded! The whole mess we started with behaves as though it were a
single resistor with a resistance of about \(3.1 \Omega \).
+
!
Can all circuits be broken down with series and parallel?
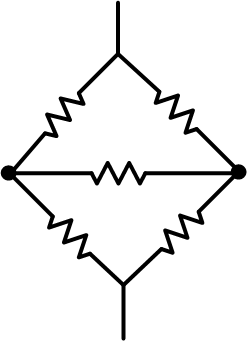
Some circuits can't be reduced with series and
parallel, such as this one
In such cases, you can use the \(Y - \Delta\) Transform to reduce it
In such cases, you can use the \(Y - \Delta\) Transform to reduce it