Recap

Organize search using a priority queue.

Queue priority is f(x) = g(x) + h(x).

• g(x) is actual cost so far
• h(x) is estimated ("heuristic") distance to goal.

Search technique demo by Xueqiao Xu.

Data structures

Data structures

• priority queue (frontier)
• table of best cost and corresponding backpointer for each state

Algorithm outline

Search loop

• pop lowest cost state off the priority queue,
• if it's a goal state, halt and return path
• otherwise
  • find its neighbors, and
  • add them to the priority queue if unvisited or new path is shorter.

When we revisit a state using a better path

• Update cost and backpointer and
• Update state's priority in the priority queue.

A* gotchas

Don't try to empty the queue

Returning immediately only works for BFS/DFS

• Push newly made goal states into the queue
• Return when you pop a goal state off the front of the queue

Use backpointer table to generate output path

Check for revisiting a state via a shorter path

To update a state's priority in the priority queue, just push a new copy of the state onto the queue.

Heuristics

Required properties for heuristic:

• quick to compute
• underestimates true distance to the goal ("admissible")

Maze:

• Straight-line distance
• Manhattan distance (change in x + change in y) if robot can't move diagonally.

Idea: simplify problem (e.g. ignore obstacles)

15-puzzle

Heuristics for the 8-puzzle or 15-puzzle

• Number of misplaced tiles
• Sum of Manhattan distances between each tile's current location and its goal location.

Why Admissibility?

Admissibility guarantees that the output solution is optimal.

When search stops:

• Best state in queue has actual cost C
• All other states in queue have estimated cost \(\ge C\).
• Estimated costs are \(\le\) actual costs.

"Suboptimal" search

• Heuristic might be a slight overestimate
• E.g. tie breaking
• Return path not guaranteed optimal
• Big speed-up if many paths of similar length

Consistency

When we reach a state via a shorter path, is that state still in the queue?

Approach #1: Don't fuss, just push updated state into the queue regardless of whether it's already there or not.

Approach #2: Ensure that the heuristic is "consistent"

Suppose we can get from s to s' with cost c(s,s'). Heuristic h is consistent if

\( h(s) \le c(s,s') + h(s') \)

I.e. g(x)+h(x) stays constant or increases as we extend path.

UCS is consistent (h is always zero).

Straight-line distance is consistent (triangle inequality).

Non-consistent examples are typically contrived.

State design

An adventure game

• Time = 5:     I'm at the Sacred Oak Tree carrying a hand axe.
• Time = 30:     I'm at the Sacred Oak Tree carrying an enchanted mithril sword, an oaken shield, two medical kits, and a Jimmy John's sandwich.

Are these the same state?

• I'm across the river from the portal and the river level is low.
• I'm across the river from the portal and the river is at flood stage.

Each state stored in the search queue must contain all information that might be relevant to extending your path towards the goal.

Reaching the goal might mean

• At a certain (x,y) position and/or
• Have enough money and/or
• Have finished some quest.

Edit distance

Good problem representation matters

Edit Distance: find the best alignment between two strings

Best: fewest character edits (delete, add, substitute)

     A L G O R   I   T H M
     A L   T R U I S T I C
         D S   A   A   S S

D = delete character
A = add character
S = substitute

Domains

• theory
• computational biology
• evaluating speech recognizers
• machine translation

Naive method

A state is a string.

An action applies one edit operation

Each state has many successors: about \( 28^9 \) possible hanges to ALGORITHM

    LGORITHM, AGORITHM, ..., ALGORIHM, ...
    BLGORITHM, CLGORITHM, ....
    AAGORITHM, ....
    ...
    ALBORJTHM, ...
    ....

Better method

A state is an alignment of the initial sections (prefixes) of the two strings.

Start state is an alignment of two empty strings

End state is an alignment of the full strings.

An action extends the alignment by one character.

• pair the next characters in the two strings
• skip a character in the first string
• skip a character in the second string

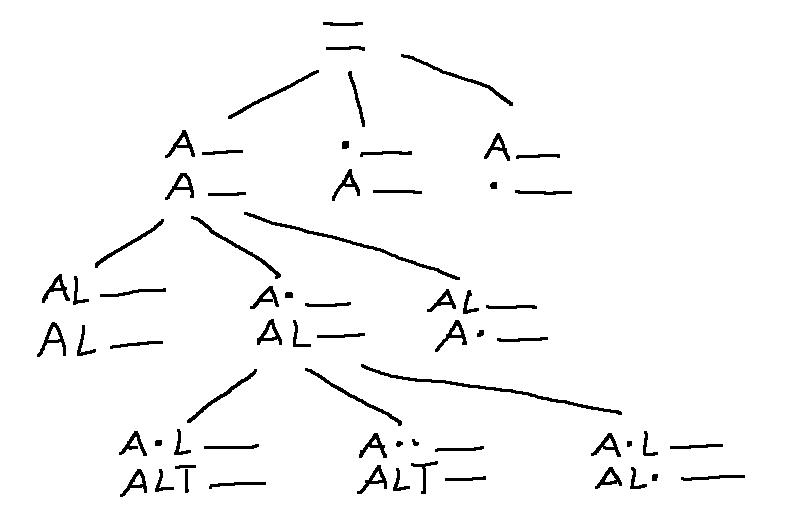
Nifty compact 2D table.

Memory efficient methods:

• Beam search: prune alignments with very bad ratings
• Compute just the distance (not the alignment) using sliding window