Problem Statement
Many animals can change their aspect ratio by extending or bunching up.
This allows animals like cats and rats to fit into small places and squeeze
through
small holes.


You will be moving an alien robot using straight-line paths between waypoints, based on this idea, to reach a goal. Specifically,
the robot lives in 2D and has three degrees of freedom:
- It can move the (x,y) position of its center of mass.
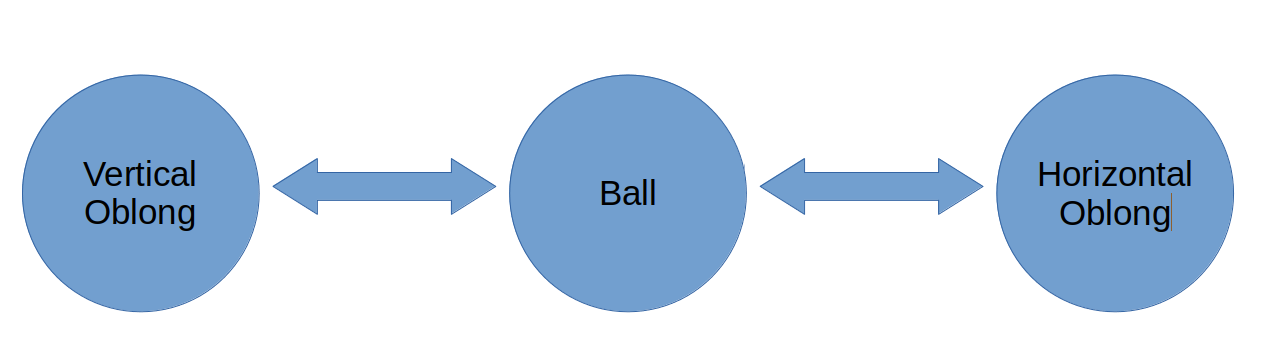
- It can switch between three forms: a long horizontal form,
a round form, and a long vertical form.
Notice that the robot cannot rotate. Also, to change from the
long vertical form to/from the long horizontal form, the robot must
go through the round form, i.e., it cannot go from its vertical oblong shape to its horizontal oblong shape directly. The robot also cannot make both a shape change and position change in the same move. These transitions must be done separately.

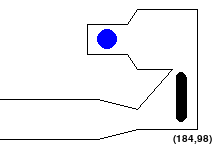

The round form is a disk (or a filled circle). The horizontal or vertical long form is a "sausage" shape, defined by
a line segment and a distance "d", i.e., any point within a given distance "d" of the LINE SEGMENT between the alien's head and tail is considered to be within the alien .
For each planning problem you will be given a 2D environment specified by:
- The size of the workspace.
- The widths of the long and round forms.
- The starting (x,y) center-of-mass position and shape of the alien.
- A list of waypoints, described by an (x, y) position.
- A list of goals, each of which is defined by an (x, y) position.
- A set of obstacles, each of which is a line segment.
You need to find a shortest path for the alien robot from its starting position
to ONE of the goal positions using straight-line paths between waypoints.
The tricky bit is that the alien may not pass through any of the
obstacles. Also, no part of the robot should go outside the workspace.
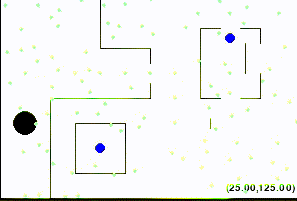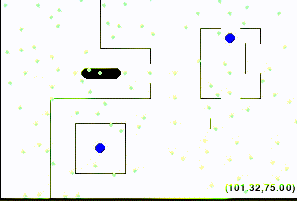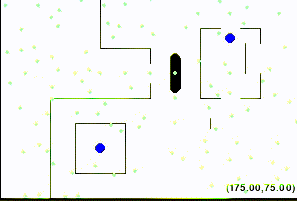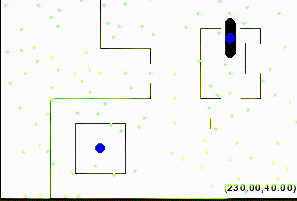
So configurations like the following are NOT allowed:
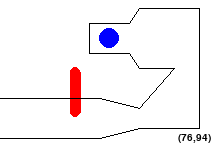
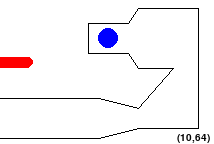
Accordingly, a straight-line path is valid if and only if it connects waypoints or goals and the alien stays in bounds and does not touch obstacles on that path.
Also note that, since we choose waypoints randomly, there may be some waypoints that are too close to the edge or obstacles for particular shapes.
We consider the maze solved once the alien's centroid is at the goal position,
as long as the alien is not violating any constraint (i.e., not out of bounds or touching a wall).
To solve MP5 and MP6, you will go through three main steps:
- Write geometry functions to check if straight-line paths are valid.
- Finish implementing a new state representation for this problem.
- Adapt your MP3/4 State and A* code to be able to search in three dimensions. (x, y, and shape)
- This is primarily a housekeeping activity to ensure your code is not hardcoded to work for a specific type of search, but can handle generic search spaces.
Search Formulation
In order to adapt A* to this problem, we need to understand how searching in the maze can be formulated as
searching through a weighted graph.
First, the nodes of the graph will include the entire state space. In this problem, the state space is a set
of tuples (x, y, shape) for all waypoints and goals (x, y) and shapes such that (x, y, shape) is in bounds and doesn't touch
an obstacle.
An edge exists between two nodes if there is a valid straight-line path between their states in the maze. Next, we define the
cost, or edge weights:
- if the centroid changes, but shape does not, the cost is the euclidean distance between the positions
- if the alien changes shape, then there is a constant cost of 10
The objective, then, is to find the lowest cost path to a goal node. However, in this case, to improve runtime, we
only consider the K-nearest neighbors in our search.
Part 0: Understanding Map configuration
Each scene (or problem) is defined in a settings file. We wrote the code to read each settings file for you.
The settings file must specify the alien's inital position, geometry of the alien in its different configurations, the waypoints (in a separate file), the goals and the edges of
the workspace.
Here is a sample scene configuration:
[Test1]
Window : (300, 200) # (Width, Height)
Obstacles : [
(0,100,100,100), #(startx,starty,endx,endy)
(0,140,100,140),
(100,100,140,110),
(100,140,140,130),
(140,110,175,70),
(140,130,200,130),
(200,130,200,10),
(200,10,140,10),
(175,70,140,70),
(140,70,130,55),
(140,10,130,25),
(130,55,90,55),
(130,25,90,25),
(90,55,90,25)
]
Goals : [
(110, 40, 10) # (x-coordinate, y-coordinate, radius)
]
Lengths: [40,0,40]
Widths: [11,25,11]
StartPoint: [30,120]
- Window: The window size for the given example map is 300x200 pixels. Note that (0, 0) is the top-left corner and (300, 200) is the bottom-right corner .
- Lengths: The lengths of the robot are in the form ['Horizontal Length', 'Ball length (always 0)', 'Vertical Length']. The length of the robot is defined by the distance between its head and tail
- Widths: widths of the robot represent the diameter of the circle that is added to the line segment "body" of the alien, i.e.. how far away from the line segment defining the body is still considered to be "inside" the robot. These are ordered in the same manner as the Lengths. These widths are twice what is returned by the get_widths function in the Alien class.
- Obstacles: There are many walls in the maze which are represented by a list of endpoints for line segments in the format (startx, starty, endx, endy)
- A list of waypoints and a list of goals specified in the form (x,y,radius). In this particular maze, there is one goal at (110,40).
- The alien is set to start at the position (30,120), in its default disk configuration
- The name of this map is Test1
Here is how the map from this configuration looks without waypoints:

You can play with the maps (stored in config file "maps/test_config.txt") by manually controlling the robot by executing the following command:
python3 mp5_6.py --human --map Test1 --config maps/test_config.txt
Feel free to modify the config files to do more self tests by adding test maps of your own.
Once the window pops up, you can manipulate the alien using the following keys:
- w / a / s / d: move the alien up / left / down/ right
- q / e: switch between horizontal, ball, and vertical forms of the alien. "q" will cycle backwards (Vertical -> Ball -> Horizontal) and "e" will cycle forwards (Horizontal -> Ball -> Vertical
While implementing your geometry.py file, you can also use this mode to manually verify parts of your solution, as the alien should turn red when touching an obstacle or out of bounds, and should turn green when validly completing the course, as shown in the initial figures.
Part 2: Adapt A*
The first part of this MP is to extend your A* code from MP 3/4 to handle our new 3D state representation, using position and shape.
Your A* code must be able to handle the possibility that there are multiple goals.
However, unlike MP 3/4, your code does not have to touch all the goals.
It should consider the maze "solved" when it reaches the first goal.
Your new A* code should be added to this file:
search.py
- astar(maze): returns optimal path in a list, which contains start and objectives. If no path found, return None.
- backtrack(visited_states, current_state): this should be similar to your MP 3/4 implementation.
To implement search, you will also need to finish the implementation of MazeState in state.py. It might help to review some of the states you made in the previous MP. Complete all of the TODOs to finish the implementation. Note that unlike the previous MP, we do not include the MST in the heuristic, because we only need to reach one goal. Given the new objective, our old heuristic would not be consistent and admissible.
NOTE: unlike MP 3/4, in this MP, the maze might not have a path! So be sure to handle this case properly and return None!
To complete the MazeState code, you will need to complete:
- euclidean_distance(a,b): which is similar to manhattan distance from MP 4
- get_neighbors(self): returns the MazeState neighbors using self.maze_neighbors. When computing move (edge) costs, note that changing shape has a cost of 10.
- __hash__(self): hash the MazeState using the centroid, shape, and goals.
- __eq__(self): check if two states are equal
- compute_heuristic(self): compute the heuristic, which is the euclidean distance to the nearest goal.
- __lt__(self, other): This method allows the heap to sort States according to f = g + h value.