CS440/ECE448 Fall 2024, MP 4: A* Search on Grids

Due: Monday, September 30, 11:59pm

I. Overview

In this assignment you will be implementing the A* search algorithm for solving GridSearch. You can safely reuse some of the code you wrote for MP3 (e.g. A* search) to solve this problem. You will see both the power of A* as an algorithm that applies to arbitrary discrete state spaces, and the power of heuristics to speed up search.

II. Getting Started

To get started on this assignment, download the template code. The template contains the following files and directories:

search.py. You will edit and submit this - your implementation of A* goes here.
state.py. You will edit and submit this - your implementation of each problem’s State goes here.
utils.py. Some utilities we provide for computing a minimum spanning tree.
maze.py. Some utilities for reading and working with grid mazes.
main.py. You will run this file to test your code.
data/. Files containing example mazes to solve

Please ONLY submit search.py and state.py (NOTE that search.py should be unchanged from MP3).

For each of the remaining parts of the assignment you will find TODOs in search.py and state.py where you need to write your own code. For example, for part V you will find TODOs marked # TODO(V). We’ve provided many comments and instructions in the code under those TODOs.

III. Single Goal Grid Search

In grid search we find a path through a 2D maze from some starting location to a single goal location. Each state is a discrete (x,y) location in the maze, and the goal is an additional location in the maze. From any location you can transition to a neighboring location assuming there is no obstacle there (obstacles colored black). In the visualization above green indicates the end of the path and red indicates the beginning. The start is capitalized and goal is lowercase.

Run the following to see mazes and navigate them yourself with the arrow keys:

python3 main.py --problem_type=GridSingle --human --maze_file=[path_to_maze_file in data/grid_single]

note: if the red-green gradient is hard for you to see, you can make the visualization use an alternative color scheme by specifying the --altcolor option

Now you will need to implement the SingleGoalGridState class. If you would like to see how the maze is built navigate to maze.py, but otherwise we’ve provided you everything you need and instructions in state.py where you have 2 “TODO(III)” in search.py to complete (copy previous code) and 4 “TODO(III)” in state.py (including in AbstractState). The heuristic we use for grid search is the manhattan distance from the current location to the goal. You may assume all actions cost 1 (meaning the dist_from_start for every neighbor should be 1 more than its parent), and this remains true for the rest of this assignment.

You can test your code with:

python3 main.py --problem_type=GridSingle --use_heuristic --maze_file=[path_to_maze_file in data/grid_single]

If you would like to also visualize the resulting solution in PyGame add the --show_maze_vis flag.

Make sure to pass in the use_heuristic flag if you wish to test your heuristic

IV. Multi Goal Grid Search

**Now we consider grid search problems with multiple goals that can be reached in any order**

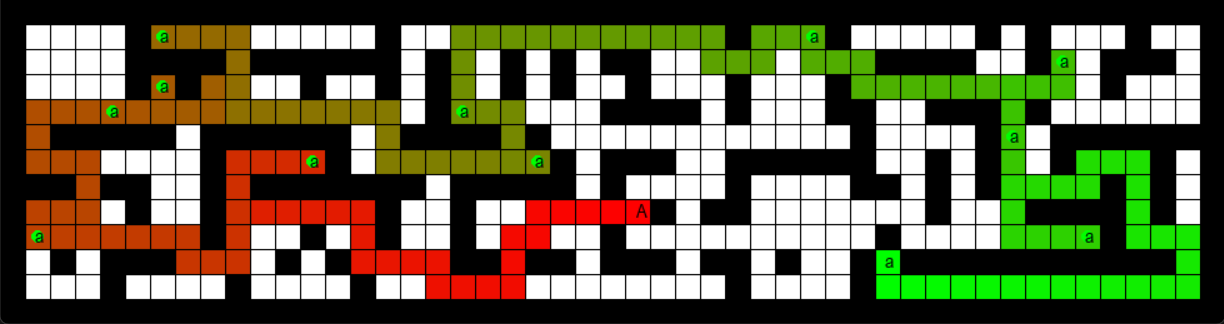
We now generalize single goal grid search to finding the shortest path in multi goal grid search. There are 2 “TODO(IV)” for you to complete in state.py.

Multiple goals requires a new heuristic. The one we use is based on the Minimum Spanning Tree (MST). Specifically, given a state and a set of goals, the heuristic cost for visiting all the goals is computed as follows:

Treat the set of goals as nodes in a complete graph
The edge weights on this graph are the distances between the goals (or approximate distances using manhattan)
To solve the multi goal search problem (i.e., a version of the Traveling Salesman Problem) we must travel AT LEAST the cost of the MST of this graph
In addition to the cost of the MST we also need to reach some goal, therefore our final heuristic is:
- h(state, goals) = manhattan(state, closest_goal) + MST(goals)

We provide you with most of the code you need to compute this MST heuristic, you can call compute_mst_cost(self.goal, manhattan) to compute the cost of the minimum spanning tree for a set of goals. Note that because computing the mst takes some time, you should store the computed mst values in the cache we provide you.

You also need to implement the other AbstractState methods of MultiGoalGridState. Be careful! They are not necessarily the same as for single goal search. In particular, think about whether self.state alone is sufficient for determining whether two states are the same. If the agent has two goals left to visit and is in position \((x,y)\) or has only one goal left to visit but is in the same position \((x,y)\), is this the same state? No! Your visited_states dictionary and frontier need to know when two states are the same, which must be reflected in the __eq__ and __hash__ methods…

You can test your code with:

python3 main.py --problem_type=GridMultiGoal --use_heuristic --maze_file=[path_to_maze_file in data/grid_multi_goal]

Once again, if you would like to also visualize the resulting solution in PyGame add the --show_maze_vis flag.

V. Multi Agent Grid Search

Now we consider grid search problems with multiple agents that all need to reach their own goals. Each agent’s start is capitalized, and their respective goals are matching lowercase characters. Again, green color is the end of the path while red is the beginning. Notice how the gradients seem less smooth - this is because the agents can now wait in place. It’s harder to see what’s going on, but here A is moving down and right, waiting for B to pass, and then going through the corridor to its goal.

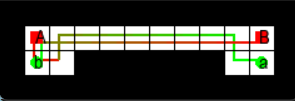
We now change our state space to include multiple agents, each of which has a single goal. We want to find the shortest path, which in this case means the sequence of actions for all agents that gets the last agent to their goal the fastest (this is called the makespan). For this problem you will finish the implementation of MultiAgentGridState. In particular, you should implement one admissible and one inadmissible heuristic, both of which must be at least as good as ours on the autograder with respect to number of states explored and path length. In get_neighbors you will now need to check for inter-agent collision, which can occur when two agents cross paths (swap cells) or try to move to the same cell at the same time. There are 2 TODO(V) for you to complete.

You can test your code with:

python3 main.py --problem_type=GridMultiAgent --use_heuristic --maze_file=[path_to_maze_file in data/grid_multi_agent] --heuristic_type=[admissible, inadmissible] --allow_waiting

Don’t forget the --allow_waiting flag, which allows agents to stay in place. Notice the --heuristic_type flag, which determines which heuristic function to use.

Once again, if you would like to also visualize the resulting solution in PyGame add the --show_maze_vis flag.

VI Submission Instructions

Submit the main part of this assignment by uploading search.py and state.py to Gradescope.

Policies

You are expected to be familiar with the general policies on the course syllabus (e.g. academic integrity) and on the top-level MP page (e.g. code style). In particular, notice that this is an individual assignment.