CS 440/ECE448 Fall 2024 Assignment 11

CS440/ECE448 Fall 2024

Assignment 11: Reinforcement Learning

Deadline: Monday, November 18th, 11:59PM

Snake
From Wikipedia

Snake is a famous video game originated in the 1976 arcade game Blockade. The player uses up, down, left and right to control the snake which grows in length (when it eats the food pellet), with the snake body and walls around the environment being the primary obstacle. In this assignment, you will train an AI agent using reinforcement learning to play a simple version of the game snake. You will implement a TD version of the Q-learning algorithm.

The external libraries required for this project are numpy and pygame. To play the game yourself and get acquainted with it, you can run

python mp11_12.py --human

Viewing Snake as a Reinforcement Learning Problem

For us to program an AI that plays Snake by itself, we first need to understand how the game can be viewed from the lens of reinforcement learning (RL). Broadly, RL can be completely described as an agent acting in an environment.

The Environment


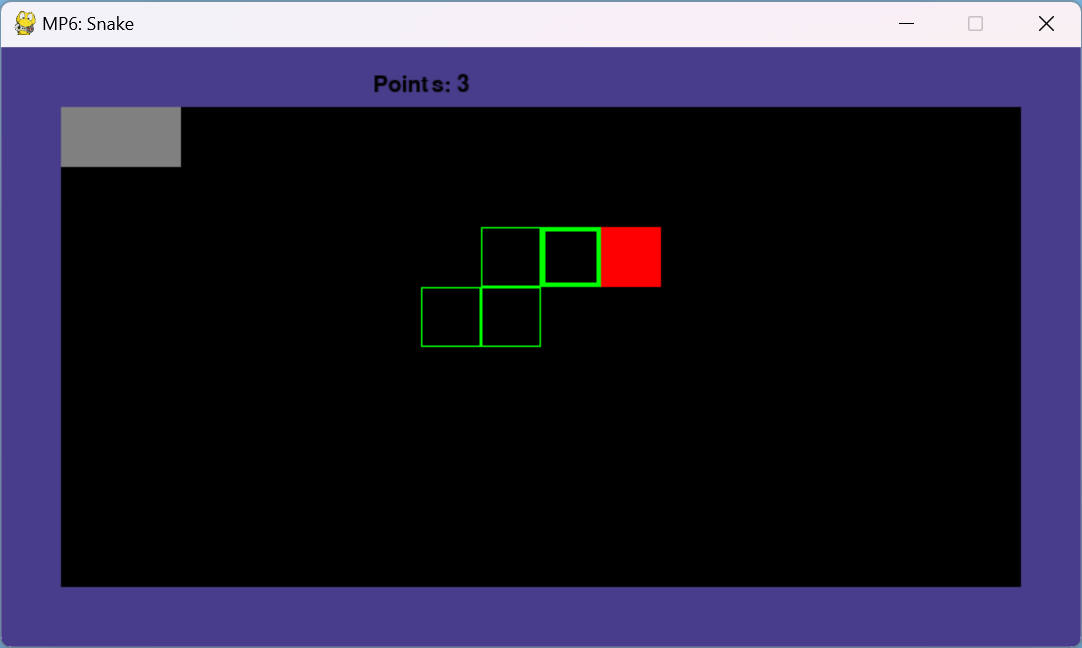
Our environment is the game board, visualized in the picture above. The green rectangle is the snake agent, and the red rectangle is the food pellet. The snake head is marked with a thicker border for easier recognition. In utils.py, We define some constants that control the pixel-wise sizes of everything:

In the above picture, we have set our game board to be 18x10, with size 1 walls, size 1 snake body, a rock at (1,1), and food. Therefore, we can treat the valid operating space of the snake to be a grid of blocks surrounded by a wall on each side. Note that the our coordinate system has the top left is (1,1). In other words, (2,2) is below and to the right of (1,1).

Implementation Tips: when computing quantities such as collisions with walls, use the top left corner of each “grid block” for its overall position. Also, check utils.py before hard coding any constants; if it is provided there, use the constant and not a hard coded value.

The objective of the game is to move the snake around the grid to collect food pellets. Every time the snake/agent eats a food pellet, the points increase by 1 and the snake’s body grows one segment. When a food pellet is eaten, a new food pellet is generated randomly on the board.

The game ends when the snake dies, after which the environment rests. The snake dies if the snake head touches any of the 4 walls, or if it touches its own body (which occurs if the head goes backwards). The snake will also die after taking \(8 *\) DISPLAY_SIZE steps without food. The DISPLAY_SIZE equals to the width times the height of the display area (18 x 10 = 180 in the above example).

The Agent

With our environment defined, we can now move on to the agent. The agent operates in the environment by defining a Markov Decision Process (MDP), which contains

  1. States: the agent’s internal representation of the environment
  2. Actions: the possible actions the agent can take in the environment
  3. Rewards: the numerical representation of the outcome of each action in the environment.

States

Each state in the MDP is a tuple (food_dir_x, food_dir_y, adjoining_wall_x, adjoining_wall_y, adjoining_body_top, adjoining_body_bottom, adjoining_body_left, adjoining_body_right).

Actions

In each timestep, your agent will choose an action from the set {UP, DOWN, LEFT, RIGHT}. You should use the respective variables defined in utils.py for these quantities.

Rewards

In each timestep, your agent will receive a reward from the environment after taking an action. The rewards are:

Q-Learning Agent

You will create a snake agent that learns how to get as many food pellets as possible without dying, which corresponds to maximizing the reward of the agent. In order to do this, we will use the Q-learning algorithm. Your task is to implement the TD Q-learning algorithm and train it on the MDP outlined above.

RL Loop

In Q-learning, instead of explicitly learning a representation for transition probabilities between states, we let the agent observe its environment, choose an action, and obtain some reward. In theory, after enough iterations, the agent will implicitly learn the value for being in a state and taking an action. We refer to this quantity as the Q-value for the state-action pair.

Explictly, our agent interacts with it’s environment in the following feedback loop:

  1. At step \(t\), the agent is in current state \(s_t\) and chooses an “optimal” action \(a_t\) using the learned values of \(Q(s_t, a)\). This acton is then executed in the environment.
  2. From the result of the action on the environment, the agent obtains a reward \(r_t\).
  3. The agent then “discretizes” this new environment by generating a state \(s_{t+1}\) based off of the new, post-action environment.
  4. With \(s_t\), \(a_t\), \(r_t\), and \(s_{t+1}\), the agent can update its Q-value estimate for the state-action pair: \(Q(s_t, a_t)\).
  5. The agent is now in state \(s_{t+1}\), and the process repeats.

Often, the notations for the current state \(s_t\) and next state \(s_{t+1}\) are written as \(s\) and \(s'\), respectively. Same for the current action \(a\) and next action \(a'\).

The Q-Update

The Q update formula is:

Q-learning Equation

where \(\gamma\) is the Temporal-Difference (TD) hyperparameter discounting future rewards, and

\[ \alpha = \frac{C}{C + N(s,a)} \]

is the learning rate controlling how much our Q estimate should change with each update. Unpacking this equation: \(C\) is a hyperparameter, and \(N(s,a)\) is the number of times the agent has been in state \(s\) and taken action \(a\). As you can see, the learning rate decays as we visit a state-action pair more often.

Choosing the Optimal Action

With its current estimate of the Q-states, the agent must choose an “optimal” action to take. However, reinforcement learning is a balancing act between exploration (visiting new states to learn their Q-values) and greed (choosing the action with the highest Q-value). Thus, during training, we use an exploration policy defined below:

\[ a^* = \text{argmax}_{a}\ \ f(Q(s,a), N(s,a))\] \[ f(Q(s,a), N(s,a)) = \begin{cases}1 & N(s,a) < Ne \\ Q(s,a) & else\end{cases}\]

where \(Ne\) is a hyperparameter. Intuitively, if an action hasn’t been explored enough times (when \(N(s,a) < Ne\)), the exploration policy chooses that action regardless of its Q-value. If there are no such actions, the policy chooses the action with the highest Q value. This policy forces the agent to visit each state and action at least \(Ne\) times.

Implementation Note: If there is a tie among actions, break it according to the priority order RIGHT > LEFT > DOWN > UP.

Implementing Your Agent

When implementing Q-learning as described above, you will need to read and update Q and N-values. For this, we have created appropriately large tables that are defined in the Agent constructor in agent.py. You should read and write from these tables, as we will be grading part of your implementation on their contents. The order of parameters in the Q and N-tables are mentioned at the end of these instructions. Alternatively, you can look in the body of create_q_table() in utils.py to see how they are initialized.

Update the N-table before the Q-table, so that the learning rate for the very first update will be a little less than 1. This is an arbitrary choice (as long as the learning rate decays with time we effectively get the same result), but it is necessary to get full-credit on the autograder. To make your code cleaner, we recommend doing the N and Q-updates right next to each other in the code.

When testing, your agent no longer needs to update either table. Your agent just needs to observe its environment, generate the appropriate state, and choose the optimal action without the exploration function.

Implementation Note: Don’t forget the edge case for updating your Q and N tables when \(t=0\). At \(t = 0\), both \(s\) and \(a\) will be None. In that case, is there anything for us to update the Q and N-tables with? Only at \(t = 1\) will \(s\) and \(a\) correspond to a state and action for which you need to update the tables.

Implementation Note: When the agent “dies”, any arbitrary action can be chosen as the game will be reset before the action can be taken. This does not need to be recorded in the Q and N tables. But, you will still need to update Q and N for the action you just took that caused the death.

Early Check

Before you start implementing the Q-learning algorithm, we recommend that you run the following tests to make sure the state are generated (discretized) correctly and your Q and N-tables are being updated correctly. This will be the primary task of MP11.

You can test this without implementing the act function. In this test, we give several specific environments to check your state generation and specific action sets to check if your Q and N-tables match ours.

Test data are stored in test_data.py. We have provided the expected Q and N-tables of these tests in the template code’s data/early_check folder. The file game_1_N.npy and game_1.npy correspond to the first game, game_2_N.npy and game_2.npy to the second game, and so on.

All other parameters are the same as the default values in utils.py. To trigger the test, run:

python mp11_12.py --early_check

Running Locally

The autograder will perform early checking for MP11, and train and test your agent given a certain set of parameters for MP12.

Some of these commands will be more relevant to MP12, but we include them for your reference here.

To see the available parameters you can set for the game, run:

python mp11_12.py --help

To train and test your agent, run:

python mp11_12.py [parameters]

To see more examples, you can take a look at MP12.

This will train the agent, test it, and save a local copy of your Q and N-tables in checkpoint.npy and checkpoint_N.npy, respectively.

By default, it will train your agent for 10,000 games and test it for 1000, though you can change these by modifying the --train-episodes and --test-episodes arguments appropriately. In addition, it will also display some example games of your trained agent at the end! (If you don’t want this to happen, just change the --show-episodes argument to 0)

You will not be tested on parameter tuning to achieve a high number of points. The autograder will pass in our choice of hyperparameter values. (So do not hard code them!) If you have implemented Q-learning correctly, you should pass all the tests with full credit. However, for fun, we recommend playing around with the hyperparameters to see how well you can train your agent!


Trained Agent

Provided Code

The file template.zip contains the supplied code (described below) and the debugging examples described above.

Do not import any non-standard libraries except pygame and numpy

Use numpy version <= 1.21.3.

You should submit the file agent.py on Gradescope. For MP11, you are only required to implement generate_state(self, environment), update_q(self, s, a, r, s_prime) and update_n(self, state, action). The function act(self, environment, points, dead) is left for MP12.

Inside agent.py, you will find the following variables/methods of the Agent class useful: