Gridworld pictures are from the U.C. Berkeley CS 188 materials (Pieter Abbeel and Dan Klein) except where noted.
Reinforcement learning is a technique for deciding which action to take in an environment where your feedback is delayed and your knowledge of the environment is uncertain. Consider, for example, a driving exam. You excute a long series of maneuvers, with a stony-faced examiner sitting next to you. At the end (hopefully) he tells you that you've passed. Reinforcement Learning can be used on a variety of AI tasks, notably board games. But it is frequently associated with learning how to control mechanical systems. It is often one component in an AI system that also uses other techniques that we've seen.
For example, we can use reinforcement learning (plus neural networks) to learn how to park a car. The car starts off behaving randomly, but is rewarded whenever it parks the car, or comes close to doing so. Eventually it learns what's required to get this reward.
We will start with a somewhat simpler model, Markov decision processes, and then upgrade to reinforcement learning.
The environment for reinforcement learning is typically modelled as a Markov Decision Process (MDP). The basic set-up is an agent (e.g. imagine a robot) moving around a world like the one shown below. Positions add or deduct points from your score. The Agent's goal is to accumulate the most points.

It's best to imagine this as a game that goes on forever. Many real-world games are finite (e.g. a board game) or have actions that stop the game (e.g. robot falls down the stairs). We'll assume that reaching an end state will automatically reset you back to the start of a new game, and no one is going to ask you to stop gaming and come to dinner, so the process continues forever.
Actions are executed with errors. So if our agent commands a forward motion, there's some chance that they will instead move sideways. In real life, actions might not happen as commanded due to a combination of errors in the motion control and errors in our geometrical model of the environment.
Eliminating the pretty details gives us a mathematician-friendly diagram:

Our MDP's specification contains
The transition function tells us the probability that a commanded action a in a state s will cause a transition to state s'.
The reward function tells us how many points we get at each state.
Our solution will be a policy \(\pi(s)\) which specifies which action to command when we are in each state. For our small example, the arrows in the diagram below show the optimal policy.

The reward function could have any pattern of negative and positive values. However, the intended pattern is
For our example above, the unmarked states have reward -0.04.
The background reward for the unmarked states changes the personality of the MDP. If the background reward is high (lower right below), the agent has no strong incentive to look for the high-reward states. If the background is strongly negative (upper left), the agent will head aggressively for the high-reward states, even at the risk of landing in the -1 location.

We'd like our policy to maximize reward over time. So something like
\(\sum_\text{sequences of states}\) P(sequence)R(sequence)
R(sequence) is the total reward for the sequence of states. P(sequence) is how often this sequence of states happens.
However, sequences of states might be extremely long or (for the mathematicians in the audience) infinitely long. Our agent needs to be able to learn and react in a reasonable amount of time. Worse, infinite sequences of values might not necessarily converge to finite values, even with the sequence probabilities taken into account.
So we make the assumption that rewards are better if they occur sooner. The equations in the next section will define a "utility" for each state that takes this into account. The utility of a state is based on its own reward and, also, on rewards that can be obtained from nearby states. That is, being near a big reward is almost as good as being at the big reward.
So what we're actually trying to maximize is
\(\sum_\text{sequences of states}\) P(sequence)U(sequence)
U(sequence) is the sum of the utilities of the states in the sequence and P(sequence) is how often this sequence of states happens.
We're going to define the utility function somewhat indirectly, via a recursive equation.
Suppose our actions were deterministic, then we could express the utility of each state in terms of the utilities of adjacent states like this:
\(U(s) = R(s) + \max_{a \in A} U(move(a,s)) \)
where move(a,s) is the state that results if we perform action a in state s. We are assuming that the agent always picks the best move (optimal policy).
Since our action does not, in fact, entirely control the next state s', we need to compute a sum that's weighted by the probability of each next state. The expected utility of the next state would be \(\sum_{s'\in S} P(s' | s,a)U(s') \), so this would give us a recursive equation
\(U(s) = R(s) + \max_{a \in A} \sum_{s'\in S} P(s' | s,a)U(s') \)
The actual equation should also include a reward delay multiplier \(\gamma\). Downweighting the contribution of neighboring states by \(\gamma\) causes their rewards to be considered less important than the immediate reward R(s). It also causes the system of equations to converge. So the final "Bellman equation" looks like this:
\(U(s) = R(s) + \gamma \max_{a \in A} \sum_{s'\in S} P(s' | s,a)U(s') \)
Specifically, this is the Bellman equation for the optimal policy.
Short version of why it converges. Since our MDP is finite, our rewards all have absolute value \( \le \) some bound M. If we repeatedly apply the Bellman equation to write out the utility of an extended sequence of actions, the kth action in the sequence will have a discounted reward \( \le \gamma^k M\). So the sum is a geometric series and thus converges if \( 0 \le \gamma < 1 \).
There's a variety of ways to solve MDP's and closely-related reinforcement learning problems:
The simplest solution method is value iteration. This method repeatedly applies the Bellman equation to update utility values for each state. Suppose \(U_k(s)\) is the utility value for state s in iteration k. Then
- initialize \(U_1(s) = 0 \), for all states s
- loop for k = 1 until the values converge
- \(U_{k+1}(s) = R(s) + \gamma \max_{a \in A} \sum_{s'\in S} P(s' | s,a)U_k(s') \)
The following pictures show how the utility values change as the iteration progresses. The discount factor \(\gamma\) is set to 0.9 and the background reward is set to 0.



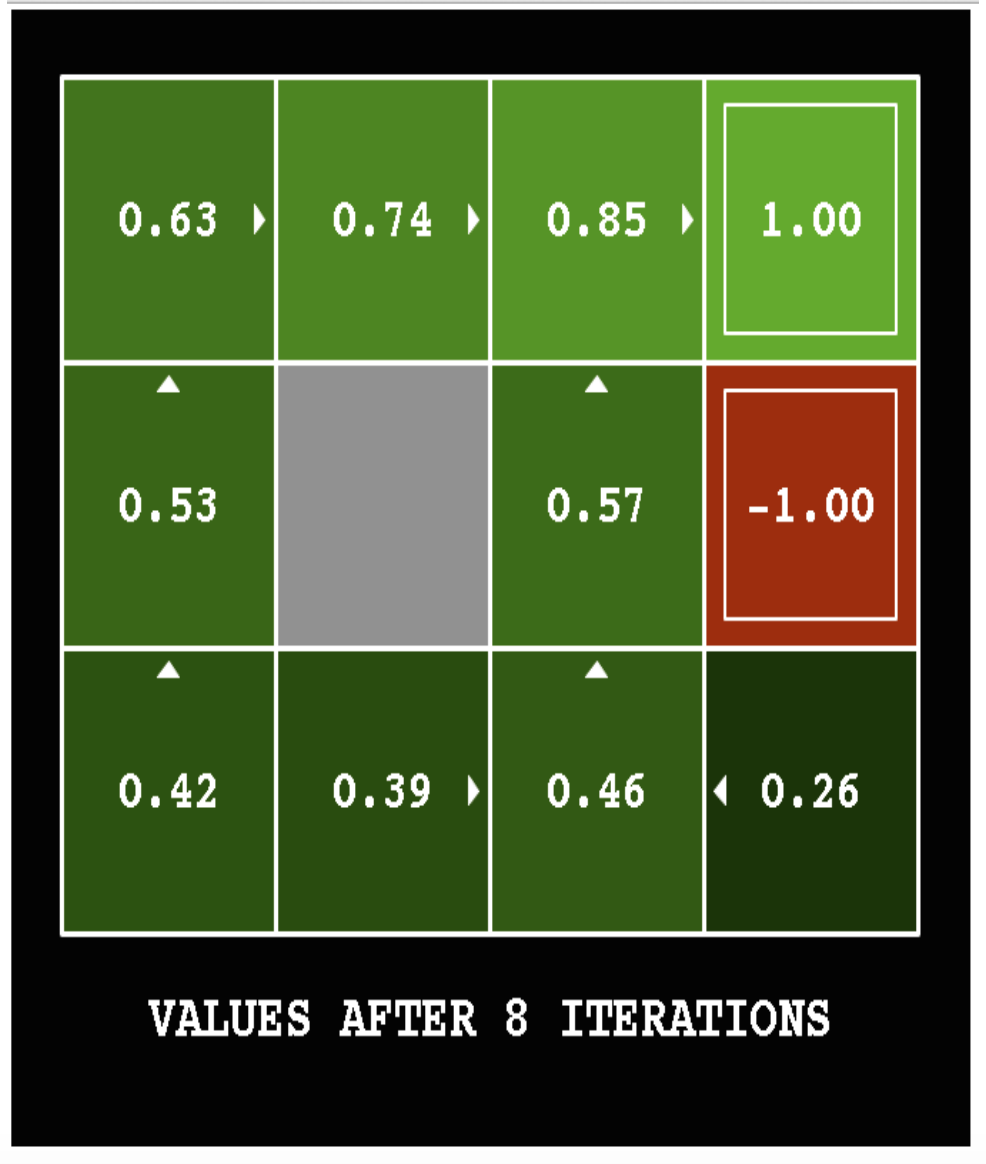

Here's the final output utilities for a variant of the same problem (discount factor \(\gamma = 1\) and the background reward is -0.04).


We can read a policy off the final utility values. We can't simply move towards the neighbor with the highest utility, because our agent doesn't always move in the direction we commanded. So the optimal policy requires examining a probabilitic sum:
\( \pi(s) = \text{argmax}_a \sum_{s'} P(s' | s,a) U(s') \)

You can play with a larger example in Andrej Karpathy's gridworld demo.
Value iteration eventually converges to the solution. The optimal utility values are uniquely determined, but there may be more than one policy consistent with them.
Some authors (notably the Berkeley course) use variants of the Bellman equation like this:
\( V(s) = \max_a \sum_{s'} P(s' | s,a) [R(s,a,s') + \gamma V(s')]\)
There is no deep change involved here. This is partly just pushing around the algebra. Also, passing more arguments to the reward function R allows a more complicated theory of rewards, i.e. depending not only on the new state but also the previous state and the action you used. If we use our simpler model of rewards, then this V(s) these can be related to our U(s) as follows
U(s) = R(s) + V(s)
Suppose that we have picked some policy \( \pi \) telling us what move to command in each state. Then the Bellman equation for this fixed policy is simpler because we know exactly what action we'll command:
Bellman equation for a fixed policy: \(\ \ U(s) = R(s) + \gamma \sum_{s'\in S} P(s' | s,\pi(s))U(s') \)
Because the optimal policy is tightly coupled to the correct utility values, we can rephrase our optimization problem as finding the best policy. This is "policy iteration". It produces the same solution as value iteration, but faster.
Specifically, the policy iteration algorithm looks like this:
Policy iteration makes the emerging policy values explicit, so they can help guide the process of refining the utility values.
The policy improvement step is easy. Just use this equation:
\( \pi(s) = \text{argmax}_a \sum_{s'} P(s' | s,a) U(s') \)
We still need to understand how to do the policy evaluation step.
Since we have a draft policy \( \pi(s) \) when doing policy evaluation, we have a simplified Bellman equation (below).
\( U(s) = R(s) + \gamma \sum_{s'} P(s' | s, \pi(s)) U(s') \)
We have one of these equations for each state s. The equations are still recursive (like the original Bellman equation) but they are now linear. So have two options for adjusting our utility function:
The value estimation approach is usually faster. We don't need an exact (fully converged) solution, because we'll be repeating this calculation each time we refine our policy \( \pi \).
One useful trick to solving Markov Decision Process is "asynchronous dynamic programming." In each iteration, it's not necessary to update all states. We can select only certain states for updating. E.g.
The details can be spelled out in a wide variety of ways.
So far, we've been solving an MDP under the assumption that we started off knowing all details of P (transition probability) and R (reward function). So we were simply finding a closed form for the recursive Bellman equation. Reinforcement learning (RL) involves the same basic model of states and actions, but our learning agent starts off knowing nothing about P and R. It must find out about P and R (as well as U and \(\pi\)) by taking actions and seeing what happens.
Obviously, the reinforcement learner has terrible performance right at the beginning. The goal is to make it eventually improve to a reasonable level of performance. A reinforcement learning agent must start taking actions with incomplete (initially almost no) information, hoping to gradually learn how to perform well. We typically imagine that it does a very long sequence of actions, returning to the same state multiple types. Its performance starts out very bad but gradually improves to a reasonable level.
A reinforcement learner may be
The latter would be safer for situations where real-world hazards could cause real damage to the robot or the environment.
An important hybrid is "experience replay." In this case, we have an online learner. But instead of forgetting its old experiences, it will
This is a way to make the most use of training experiences that could be limited by practical considerations, e.g. slow, costly, dangerous.
A reinforcement learner repeats the following sequence of steps:
There are two basic choices for the "internal representation":
We'll look at model-free learning next lecture.
A model based learner operates much like a naive Bayes learning algorithm, except that it has to start making decisions as it trains. Initially it would use some default method for picking actions (e.g. random). As it moves around taking actions, it tracks counts for what rewards it got in different states and what state transitions resulted from its commanded actions. Periodically it uses these counts to
Gradually transition to using our learned policy \(\pi\).
This obvious implementation of a model-based learner tends to be risk-averse. Once a clear policy starts to emerge, it has a strong incentive to stick to its familiar strategy rather than exploring the rest of its environment. So it could miss very good possibilities (e.g. large rewards) if it didn't happen to see them early.
To improve performance, we modify our method of selecting actions:
"Explore" could be implemented in various ways, such as
The probability of exploring would typically be set high at the start of learning and gradually decreased, allowing the agent to settle into a specific final policy.
The decision about how often to explore must depend on the state s. States that are easy to reach from the starting state(s) end up explored very early, when more distant states may have barely been reached. For each state s, it's important to continue doing significant amounts of exploration until each action has been tried (in s) enough times to have a clear sense of what it does.
We've see model-based reinforcement learning. Let's now look at model-free learning. For reasons that will become obvious, this is also known as Q-learning.
A useful tutorial from Travis DeWolf: Q learning
\( U(s) = R(s) + \gamma \max_a \sum_{s'} P(s' | s,a)U(s') \)
Where
For Q learning, we split up and recombine the Bellman equation. First, notice that we can rewrite the equation as follows, because \( \gamma \) is a constant and R(s) doesn't depend on which action we choose in the maximization.
\( U(s) = \max_a [\ R(s) + \gamma \sum_{s'} P(s' | s,a)U(s')\ ] \)
Then divide the equation into two parts:
Q(s,a) tells us the value of commanding action a when the agent is in state s. Q(s,a) is much like U(s), except that the action is fixed via an input argument. As we'll see below, we can directly estimate Q(s,a) based on experience.
To get the analog of the Bellman equation for Q values, we recombine the two sections of the Bellman equation in the opposite order. So let's make a version of the second equation referring to the following state s' (since it's true for all states). a' is an action taken starting in this next state s'.
\( U(s') = \max_{a'} Q(s',a') \)
Then substitute the second equation into the first
\( Q(s,a) = R(s) + \gamma \sum_{s'} P(s' | s, a) \max_{a'\in A} Q(s',a') \)
This formulation entirely removes the utility function U in favor of the function Q. But we still have an inconvenient dependence on the transition probabilities P.
To figure out how to remove the transition probabilities from our update equation, assume we're looking at one fixed choice of state s and commanded action a and consider just the critical inner part of the expression:
\( \sum_{s'} P(s' | s, a) \max_{a'} Q(s',a') \)
We're weighting the value of each possible next state s' by the probability P(s' | s,a) that it will happen when we command action a in state s.
Suppose that we command action a from state s many times. For example, we roam around our environment, occasionally returning to state s. Then, over time, we'll transition into s' a number of times proportional to its transition probability P(s' | s,a). So if we just average
\( \max_{a'} Q(s',a')\)
over an extended sequence of actions, we'll get an estimate of
\( \sum_{s'} P(s' | s, a) \max_{a'} Q(s',a') \)
So we can estimate Q(s,a) by averaging the following quantity over an extended sequence of timesteps t
\( Q(s,a) = R(s) + \gamma \max_{a'} Q(s',a') \)
We need these estimates for all pairs of state and action. In a realistic training sequence, we'll move from state to state, but keep returning periodically to each state. So this averaging process should still work, as long as we do enough exploration.
The above assumes implicitly that we have a finite sequence of training data, processed as a batch, so that we can average up groups of values in the obvious way. How do we do this incrementally as the agent moves around?
One way to calculate the average of a series of values \( V_1 \ldots V_n \) is to start with an initial estimate of zero and average in each incoming value with a an appropriate discount. That is
Now suppose that we have an ongoing sequence with no obvious endpoint. Or perhaps the sequence is so long that the world might gradually change, so we'd like to slowly adapt to change. Then we can do a similar calculation called a moving average:
The influence of each input decays gradually over time. The effective size of the averaging window depends on the constant \(\alpha \).
If we use this to average our values Q(s,a), we get an update method that looks like:
Our update equation can also be written as
\( Q(s,a) = Q(s,a) + \alpha [R(s) - Q(s,a) + \gamma \max_{a'} Q(s',a')] \)
We can now set up the full "temporal difference" algorithm for choosing actions while learning the Q values.
The obvious choice for an action to command in step 1 is
\( \pi(s) = \text{argmax}_{a} Q(s,a) \)
But recall from a previous lecture that the agent also needs to explore. So a better method to use in step 1 is
The best balance between these two possibilities depends on the state and action. We should do more random exploration in states that haven't been sufficiently explored, with a bias towards choosing actions that haven't been sufficiently explored.
Adding exploration creates an inconsistency in our TD algorithm.
So the update in step 3 is based on a different action from the one actually chosen by the agent. In particular, our construction of the update method assumes that we always followed our currently best policy pi, but our action selection method also includes exploration. So occasionally the agent does random things that don't follow policy.
The SARSA ("State-Action-Reward-State-Action") algorithm adjusts the TD algorithm to align the update with the actual choice of action. The algorithm looks like this, where (s,a) is our current state and action and (s',a') is the following state and action.
So we're unrolling a bit more of the state-action sequence before doing the update. Our update uses the actions that the agent chose rather than maximizing over all possible actions that the agent might choose.
Here's an example from Travis DeWolf that nicely illustrates the difference between SARSA and TD update. The agent is prone to occasional random motions, because it likes to explore rather than just following its optimal policy. The TD algorithm assumes it will do a better job of following policy, so it sends the agent along the edge of the hazard and it regularly falls in. The SARSA agent (correctly) doesn't trust that it will stick to its own policy. So it stays further from the hazard, so that the occasional random motion isn't likely to be damaging.

Mouse (blue) tries to get cheese (green) without falling in the pit of fire (red).

Trained using TD update

Trained using SARSA
There are many variations on reinforcement learning. Especially interesting ones include
Spider robot from Yamabuchi et al 2013
playing Atari games (V. Mnih et al, Nature, February 2015)