CS440/ECE448 Fall 2022, Homework 2: A* Search

Due: Friday, September 30, 11:59pm

I. Overview

In this assignment you will be implementing the A* search algorithm for solving 3 different search problems - EightPuzzle, WordLadder, and GridSearch. Your single implementation of the algorithm will work for all 3 problems, by properly instantiating an AbstractState class for each of them. You will see both the power of A* as an algorithm that applies to arbitrary discrete state spaces, and the power of heuristics to speed up search.

II. Getting Started

To get started on this assignment, download the template code. The template contains the following files and directories:

search.py. You will edit and submit this - your implementation of A* goes here.
state.py. You will edit and submit this - your implementation of each problem’s State goes here.
utils.py. Some utilities we provide.
maze.py. Some utilities for reading and working with grid mazes.
main.py. You will run this file to test your code.
data/eight_puzzle. Text files containing example problems for the eight puzzle task
data/word_ladder. Text file containing example problems for the word ladder task, along with a dictionary of english words
data/mazes. Files containing example mazes to solve

Please ONLY submit search.py and state.py.

For each of the remaining parts of the assignment you will find TODOs in search.py and state.py where you need to write your own code. For example, for part III you will find TODOs marked # TODO(III). We’ve provided many comments and instructions in the code under those TODOs.

III. Implementing Best First Search (and WordLadder)

**WordLadder: find a sequence of English words from some starting word (i.e., “head”) to some goal word (i.e., “tail”), where consecutive words differ by only one letter**

There are 2 “TODO(III)” in search.py.

Your first task is to implement a generic best first search algorithm in the method best_first_search(starting_state) in search.py. Your implementation should:

use a priority queue (heapq) of states on the “frontier”
use a dictionary that keeps track of the states which have been visited
iteratively search through the neighbors of each state until you find the shortest path to the goal
if you do not find the goal you should return an empty list

Notice that the input to best_first_search is just a starting state. You may be wondering:

How do you find the neighbors of a state?
How do you know if you’ve reached the goal?
How can you hash state objects into a dictionary?
How can you push state objects onto a sorted heap?

Now you should look at state.py, there are 3 “TODO(III)” in state.py. These questions should be answered by the comments in the code under those TODOs. You should first read through our AbstractState class, then look at an instantiation of this class called WordLadderState.

In order to test your search code we’ve provided almost all of WordLadderState. Once you’ve filled in the missing code, and implemented the search code, you should be able to test your algorithm. Make sure your algorithm works on all the provided tests before moving on to the next parts. If it works you will not have to touch it again!

Run best_first_search on all WordLadder problems:

python3 main.py --problem_type=WordLadder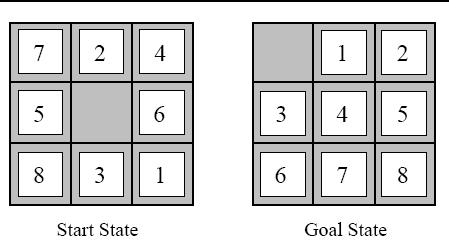

IV. EightPuzzle

EightPuzzle: find a sequence of tile moves that put each number in its final position (right) from some example starting position (left). You can only move a tile that is adjacent to the empty square into the empty square.

Now move on to EightPuzzleState, we’ve provided some but not all of the code you’ll need here. There are 4 “TODO(IV)” in state.py.

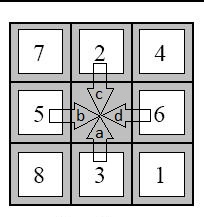
Implement manhattan(a,b)
- you will need this for computing the heuristic, you will also need this for parts V and VI
Implement EightPuzzleState.get_neighbors(self)
- In EightPuzzle the possible actions are to move an adjacent tile into the empty square (indicated by a zero)
- There are up to 4 possible neighbors for each state, though if the empty tile is on the edge there are fewer
- The order you add states onto the frontier matters for tiebreaking
  - You should add them in the order [below, left, above, right], where for example “below” corresponds to moving the empty tile down (moving the tile below the empty tile up). See the figure below for details.
Implement EightPuzzleState.compute_heuristic(self)
- There is more than one valid heuristic for this problem, the one we ask you to implement is Manhattan
  - Manhattan heuristic for Eight Puzzle is the sum of the manhattan distances from each tile to its goal location (not counting the empty tile)
  - This is a valid heuristic because each tile must move at least its manhattan distance times to reach its goal, and you can only move one tile at a time.
Implement EightPuzzleState.__lt__(self, other)

Run best_first_search on EightPuzzle problems (all puzzles with puzzle_len=N can be solved in N steps):

python3 main.py --problem_type=EightPuzzle --puzzle_len=5

You can choose any puzzle length among [5, 10, 27].

Please add neighbors in this move order (a,b,c,d) to be consistent with our implementation. The manhattan heuristic for this example is: 3 (number of moves 1 is away from its goal location) + 1 + 2 + 2 + 2 + 3 + 3 + 2 (number of moves 8 is away from its goal location) = 18. This means this puzzle takes at least 18 moves to solve.

V. Single Goal Grid Search

In grid search we find a path through a 2D maze from some starting location to a single goal location. Each state is a discrete (x,y) location in the maze, and the goal is an additional location in the maze. From any location you can transition to a neighboring location assuming there is no obstacle there (colored black). In the visualization above green indicates the end of the path and red indicates the beginning.

Finally we come to GridSearch.

Run the following to see mazes and navigate them yourself with the arrow keys:

python3 main.py --problem_type=GridSingle --human --maze_file=[path_to_maze_file in data/mazes/grid_single]

note: if the red-green gradient is hard for you to see, you can make the visualization use an alternative color scheme by specifying the --altcolor option

Now you will need to implement the SingleGoalGridState class. If you would like to see how the maze is built navigate to maze.py, but otherwise we’ve provided you everything you need and instructions in state.py where you have 4 “TODO(V)” to complete. The heuristic we use for grid search is the manhattan distance from the current location to the goal.

You can test your code with:

python3 main.py --problem_type=GridSingle --maze_file=[path_to_maze_file in data/mazes/grid_single]

If you would like to also visualize the resulting solution in PyGame add the --show_maze_vis flag.

VI. Multi Goal Grid Search

**Now we consider grid search problems with multiple goals that can be reached in any order**

We now generalize single goal grid search to multi goal grid search. There are 5 “TODO(VI)” for you to complete in state.py.

Multiple goals requires a new heuristic. The one we use is the Minimum Spanning Tree (MST). Specifically, given a state and a set of goals, the heuristic cost for visiting all the goals is computed as follows:

Treat the set of goals as nodes in a complete graph
The edge weights on this graph are the distances between the goals (or approximate distances using manhattan)
To solve the multi goal search problem (i.e., a version of the Travelling Salesman Problem) we must travel AT LEAST the cost of the MST of this graph
In addition to the cost of the MST we also need to reach the first goal, therefore our final heuristic is:
- h(state, goals) = manhattan(state, closest_goal) + MST(goals)

We provide you with most of the code you need to compute this MST heuristic, you can call compute_mst_cost(self.goal, manhattan) to compute the cost of the minimum spanning tree for a set of goals. Note that because computing the mst takes some time, you should store the computed mst values in the cache we provide you.

You can test your code with:

python3 main.py --problem_type=GridMulti --maze_file=[path_to_maze_file in data/mazes/grid_multi]

You can also check backwards compatibility by running GridMulti on a maze file with only one goal.

VII Submission Instructions

Submit the main part of this assignment by uploading search.py and state.py to Gradescope.

Policies

You are expected to be familiar with the general policies on the course syllabus (e.g. academic integrity) and on the top-level MP page (e.g. code style). In particular, notice that this is an individual assignment.