A good search algorithm must be coupled with a good representation of the problem. So transforming to a different state graph model may dramatically improve performance. We'll illustrate this with finding edit distance, and then see another example when we get to classical planning.
Problem: find the best alignment between two strings, e.g. "ALGORITHM" and "ALTRUISTIC". By "best," we mean the alignment that requires the fewest editing operations (delete char, add char, substitute char) to transform the first word into the second. We can get from ALGORITHM to ALTRUISTIC with six edits, producing the following optimal alignment:
A L G O R I T H M
A L T R U I S T I C
D S A A S S
D = delete character
A = add character
S = substitute
Versions of this task appear in
Each state is a string. So the start state would be "algorithm" and the end state is "altruistic." Each action applies one edit operation, anywhere in the word.
In this model, each state has a very large number of successors. So there are about \( 28^9 \) single-character changes you could make to ALGORITHM, resulting in words like:
LGORITHM, AGORITHM, ..., ALGORIHM, ...
BLGORITHM, CLGORITHM, ....
AAGORITHM, ....
...
ALBORJTHM, ...
....
This massive fan-out will cause search to be very slow.
A better representation for this problem explores the space of partial matches. Each state is an alignment of the initial sections (prefixes) of the two strings. So the start state is an alignment of two empty strings, and the end state is an alignment of the full strings.
In this representation, each action extends the alignment by one character. From each state, there are only three legal moves:
Here's part of the search tree, showing how we extend the alignment with each step. (A dot represents a skipped character.)
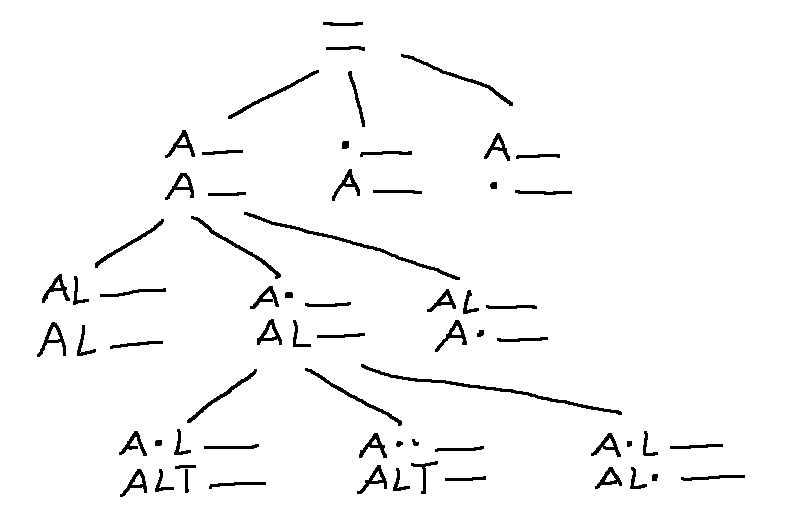
In this specific case, we can pack our work into a nifty compact 2D table.
This algorithm can be adapted for situations where the search space is too large to maintain the full alignment table. for example, we may need to match DNA sequences that are \(10^5\) characters long.
For more detail, see Wikipedia on edit distance and Jeff Erickson's notes.