How do we compute a path in a configuration space?
For simple 2D examples, e.g. MP 2, we can digitize the configuration space positions and use a digitized maze search algorithm. However, this approach scales very badly.
Normally we convert configuration space into a graph representation containing
These graph representations are compact and can be searched efficiently.
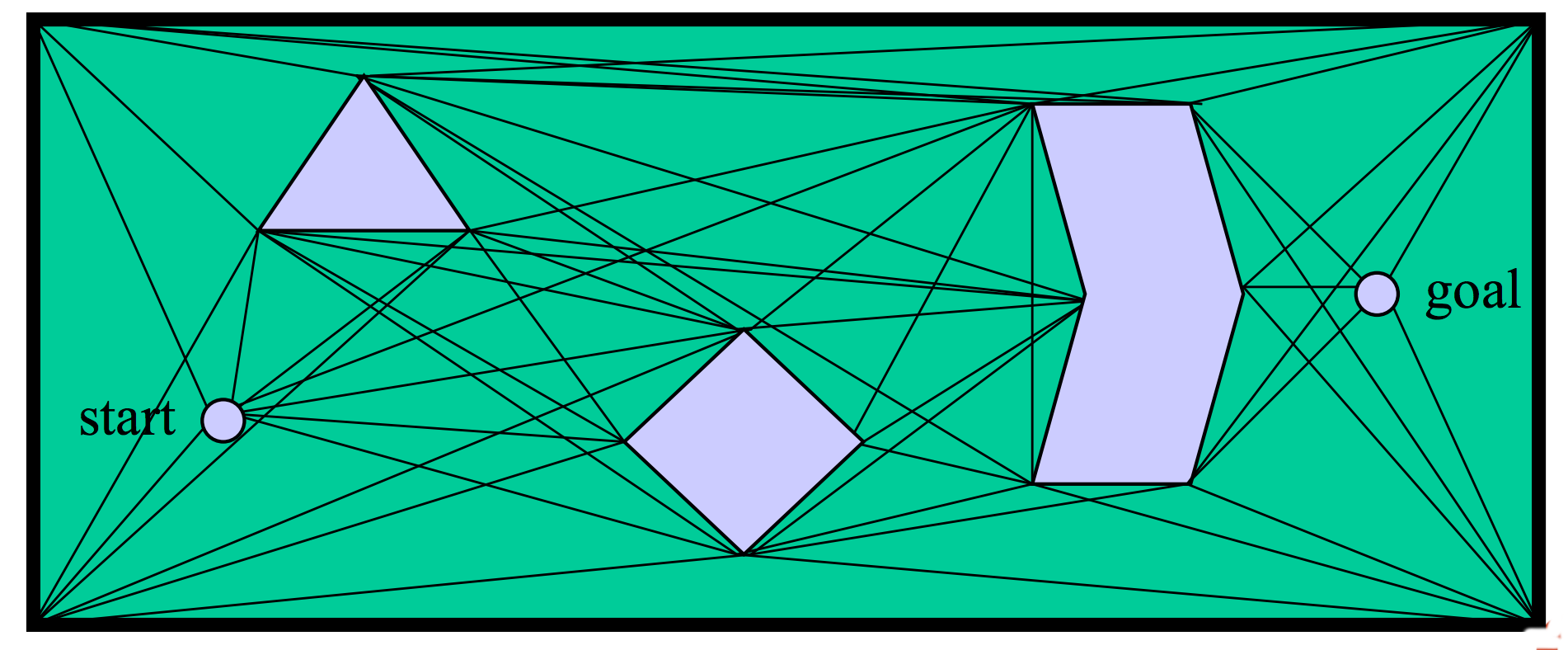
One graph-based approach uses vertices of objects as waypoints. Edges are straight lines connecting vertices. This "visibility graph" can be constructed incrementally, directly from a polygonal representation of the obstacles:
(from Howie Choset's book)
This type of representation was popular in early configuration space algorithms. It produces paths of minimal length. However, these paths aren't very safe because they skim the edges of obstacles. It's risky to get too close to obstacles. We could easily hit the obstacle if there are any errors in our model of our shape, our position, and/or the obstacle position. For most practical applications, it's better to have a somewhat longer path that is reasonably short and doesn't come too close to obstacles.
Another class of methods converts freespace into a skeleton that goes through the middle of regions, called a "roadmap". Paths via the skeleton stay far from obstacles, so they tend to be safe but perhaps overly long.
The "Generalized Voronoi Diagram" places the skeleton along curves that are equidistant from two or more obstacles. The waypoints are the places where these curves intersect.
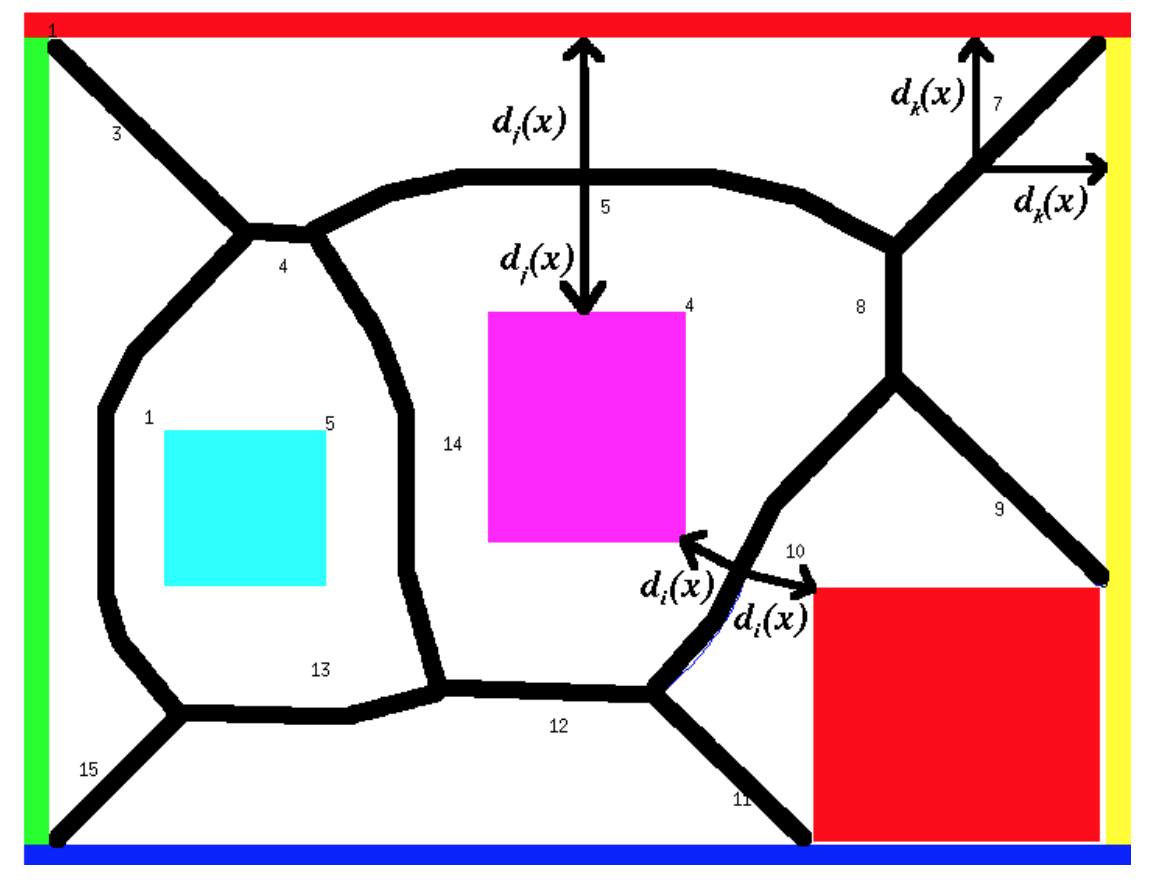(from Howie Choset)
The cell decomposition below divides free space somewhat more arbitrarily into trapezoids aligned with the coordinate axes. Waypoints are then located in the middle of each trapezoid and the middles of its edges.
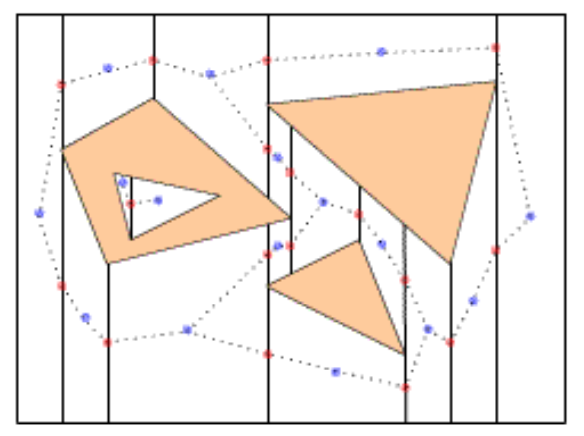(from Philippe Cheng, MIT, 2001)
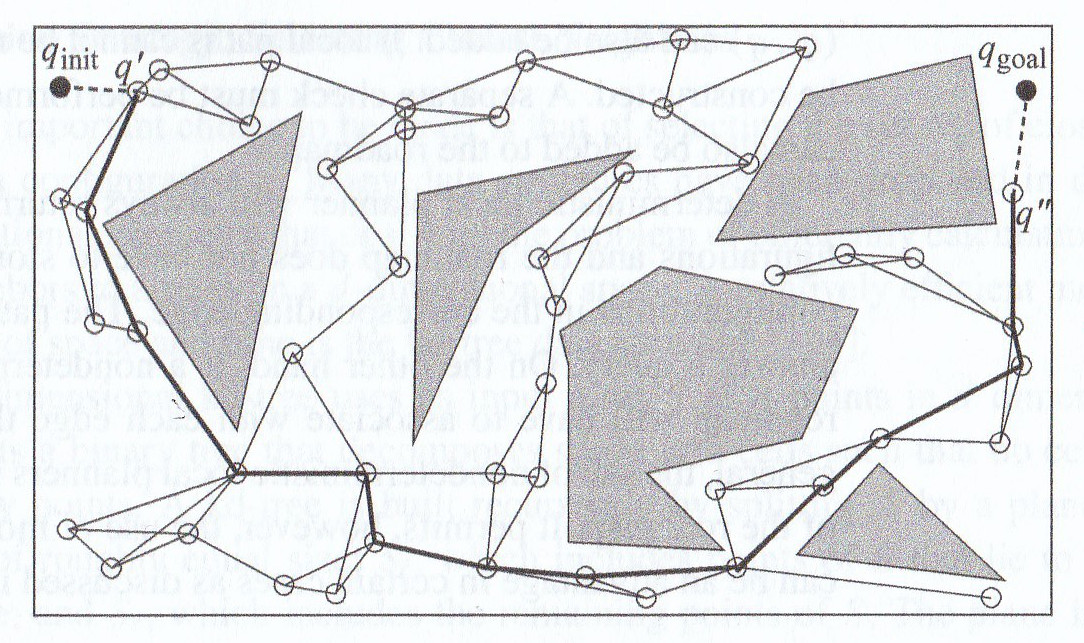
A roadmap for a configuration space is usually precomputed and then used to plan many paths, e.g. as the robot moves around its environment. The start and goal of the path will typically not be on the roadmap. So the path is constructed in three parts:
Paths assembled from roadmap edges may be longer than needed, and the edges aren't joined together smoothly. Sharp changes in orientation may be impossible for the robot to execute and/or cause excessive wear on the joints. So it is standard practice to optimize them (e.g. by smoothing the curve) in a post-processing step.
Recent algorithms create roadmaps more efficiently by sampling the configuration space without every computing the details of all the obstacles. Specifically we
There are fast algorithms for deciding whether a specific point is inside any obstacle. If waypoints are close together, there are also simple methods for connecting them, e.g. check whether the straight line between them is in free space.
Here is a probabilistic roadmap for a simple planning problem (left) and a plan constructed using it (right).
(
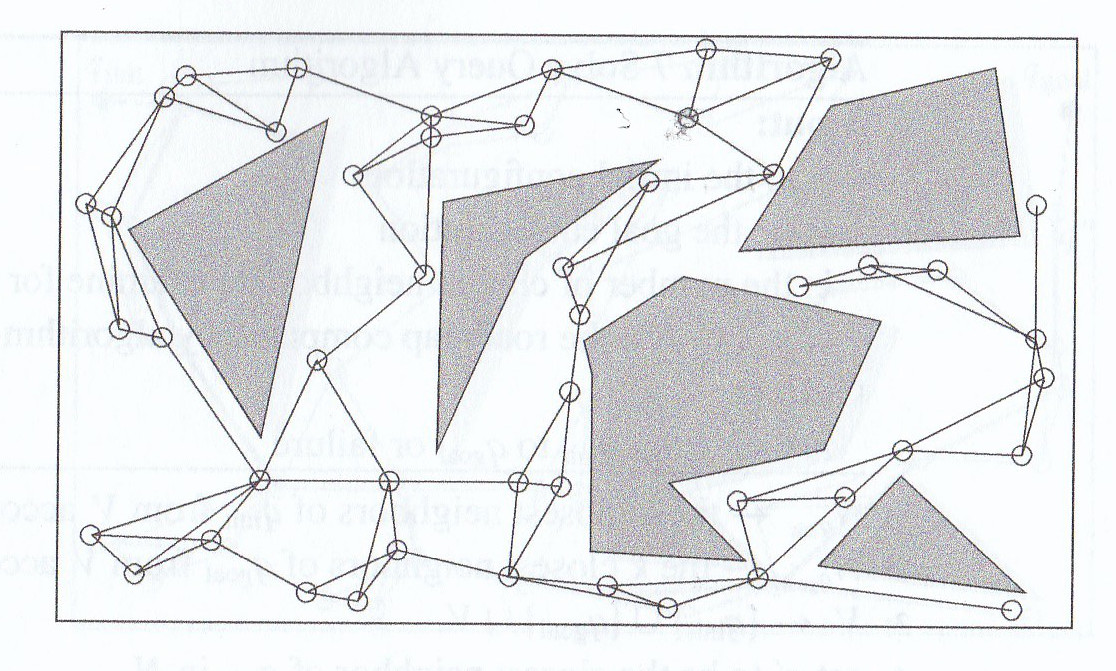(from Howie Choset book)