Temporal difference (TD) learning

We can now set up the full "temporal difference" algorithm for choosing actions while learning the Q values.

• Q(s,a) = 0 for all s and all a
• for t = 1 to forever
  1. in the current state s, select an action a
  2. observe the reward R(s) and the next state s'
  3. update our Q values \( Q(s,a) = Q(s,a) + \alpha [R(s) - Q(s,a) + \gamma \max_{a'} Q(s',a')] \)

The obvious choice for an action to command in step 1 is

\( \pi(s) = \text{argmax}_{a} Q(s,a) \)

But recall from a previous lecture that the agent also needs to explore. So a better method is

• Sometimes choose \( \pi(s) = \text{argmax}_{a} Q(s,a) \)
• Sometimes choose a random (or semi-random) action

The best balance between these two possibilities depends on the state and action. We should do more random exploration in states that haven't been sufficiently explored, with a bias towards choosing actions that haven't been sufficiently explored.

What's wrong with TD?

Adding exploration creates an inconsistency in our TD algorithm.

• The maximization \( \max_{a'} Q(s',a') \) in step 3 assumes we pick the action that will yield the highest value, but
• Step 1 doesn't always choose the action that currently seems to have the highest value.

So the update in step 3 is based on a different action from the one actually chosen by the agent. In particular, our construction of the update method assumes that we always followed our currently best policy pi, but our action selection method also includes exploration. So occasionally the agent does random things that don't follow policy.

SARSA

The SARSA ("State-Action-Reward-State-Action") algorithm adjusts the TD algorithm to align the update with the actual choice of action. The algorithm looks like this, where (s,a) is our current state and action and (s',a') is the following state and action.

• Q(s,a) = 0 for all s and all a
• pick an initial state s and initial action a
• for t = 1 to forever
  • observe the reward R(s) and the next state s'
  • from next state s', select next action a'
  • update our Q values using \( Q(s,a) = Q(s,a) + \alpha [R(s) - Q(s,a) + \gamma Q(s',a')] \)
  • (s,a) = (s',a')

So we're unrolling a bit more of the state-action sequence before doing the update. Our update uses the actions that the agent chose rather than maximizing over all possible actions that the agent might choose.

SARSA vs. TD update

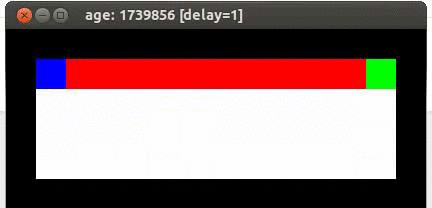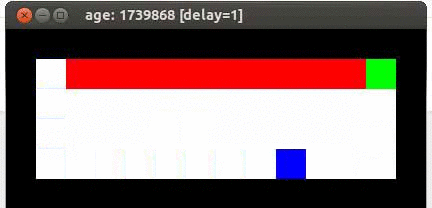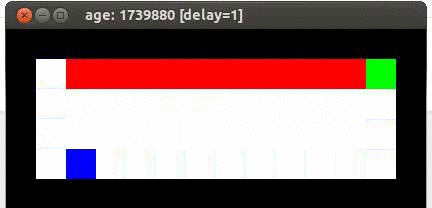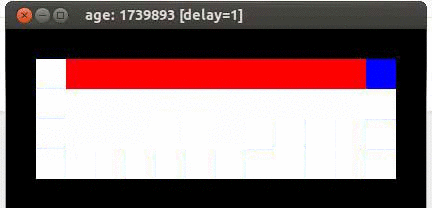
Here's an example from Travis DeWolf that nicely illustrates the difference between SARSA and TD update. The agent is prone to occasional random motions, because it likes to explore rather than just following its optimal policy. The TD algorithm assumes it will do a better job of following policy, so it sends the agent along the edge of the hazard and it regularly falls in. The SARSA agent (correctly) doesn't trust that it will stick to its own policy. So it stays further from the hazard, so that the occasional random motion isn't likely to be damaging.

Mouse (blue) tries to get cheese (green) without falling in the pit of fire (red).

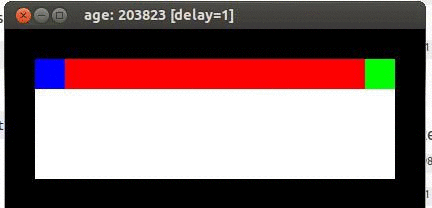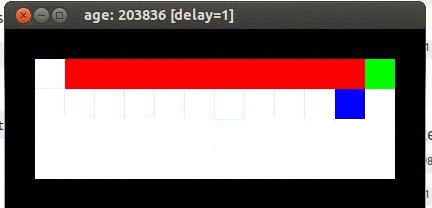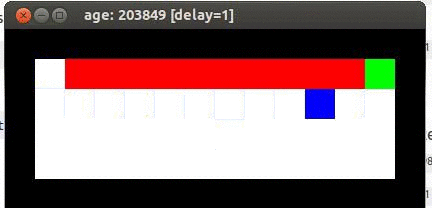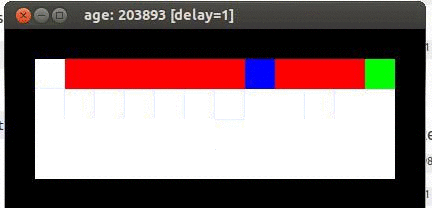
Trained using TD update

Trained using SARSA

Tweaks and extensions

There are many variations on reinforcement learning. Especially interesting ones include

• use features to model states, so we can predict values for unseen states based on familiar states that are similar in some way
• deploy deep learning (e.g. to learn a mapping from features to Q values)
• imitate an expert rather than having numerical rewards.

Reinforcement Learning Demos and Applications

Stanford helicopter

Spider robot from Yamabuchi et al 2013

playing Atari games (V. Mnih et al, Nature, February 2015)