So far, we've seen some systems containing more than one classifier unit, but each unit was always directly connected to the inputs and an output. When people say "neural net," they usually mean a design with more than layer of units, including "hidden" units which aren't directly connected to the output. Early neural nets tended to have at most a couple hidden layers (as in the picture below). Modern designs typically use many layers.
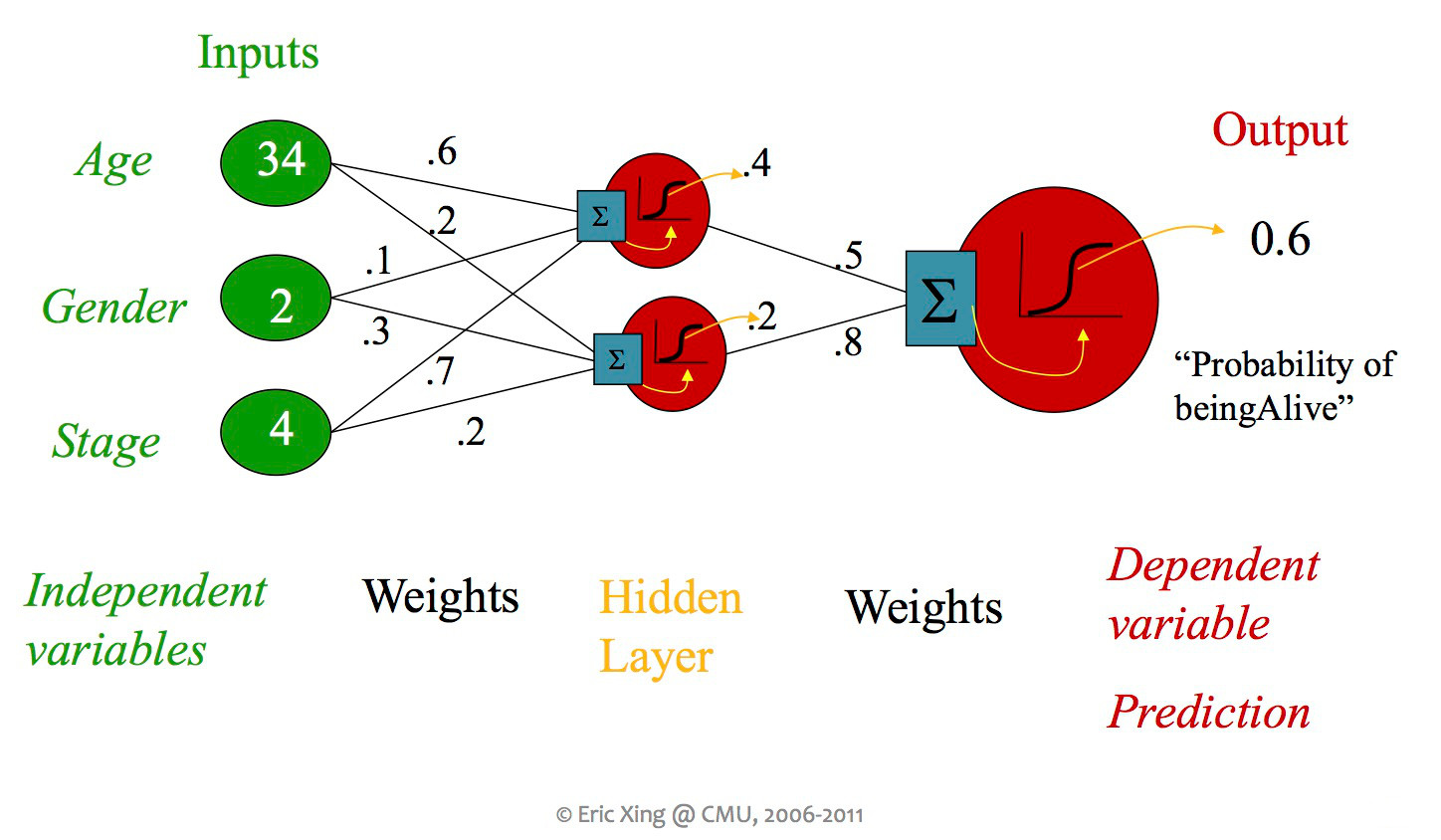
from Eric Xing via Matt Gormley
A single unit in a neural net can look like any of the linear classifiers we've seen previously. Moreover, different layers within a neural net design may use types of units (e.g. different activation functions). However, modern neural nets typically use entirely differentiable functions, so that gradient descent can be used to tune the weights.
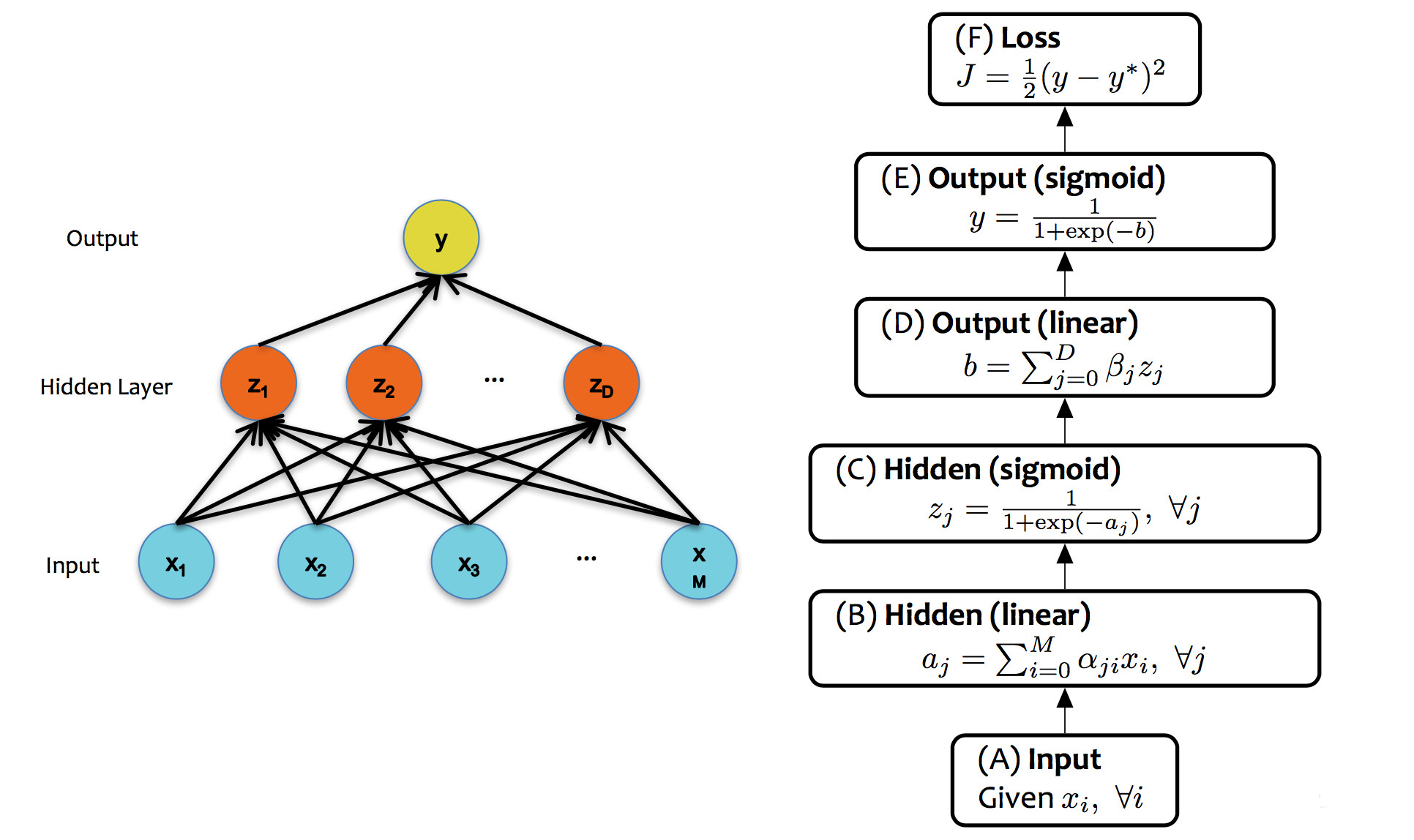
from Matt Gormley
Notice two things about this design. First, each layer has its own activation function, but there is only one loss function, at the very end. Second, the activation functions are non-linear. If we had linear activation functions, we could squash the whole network down into one linear function, so we'd be back to having only linear classification boundaries.
The core ideas in neural networks go back decades. Some of their recent success is due to better understanding of design and/or theory. But perhaps the biggest reasons have to do with better computer hardware and better library support for the annoying mechanical parts of the computation.
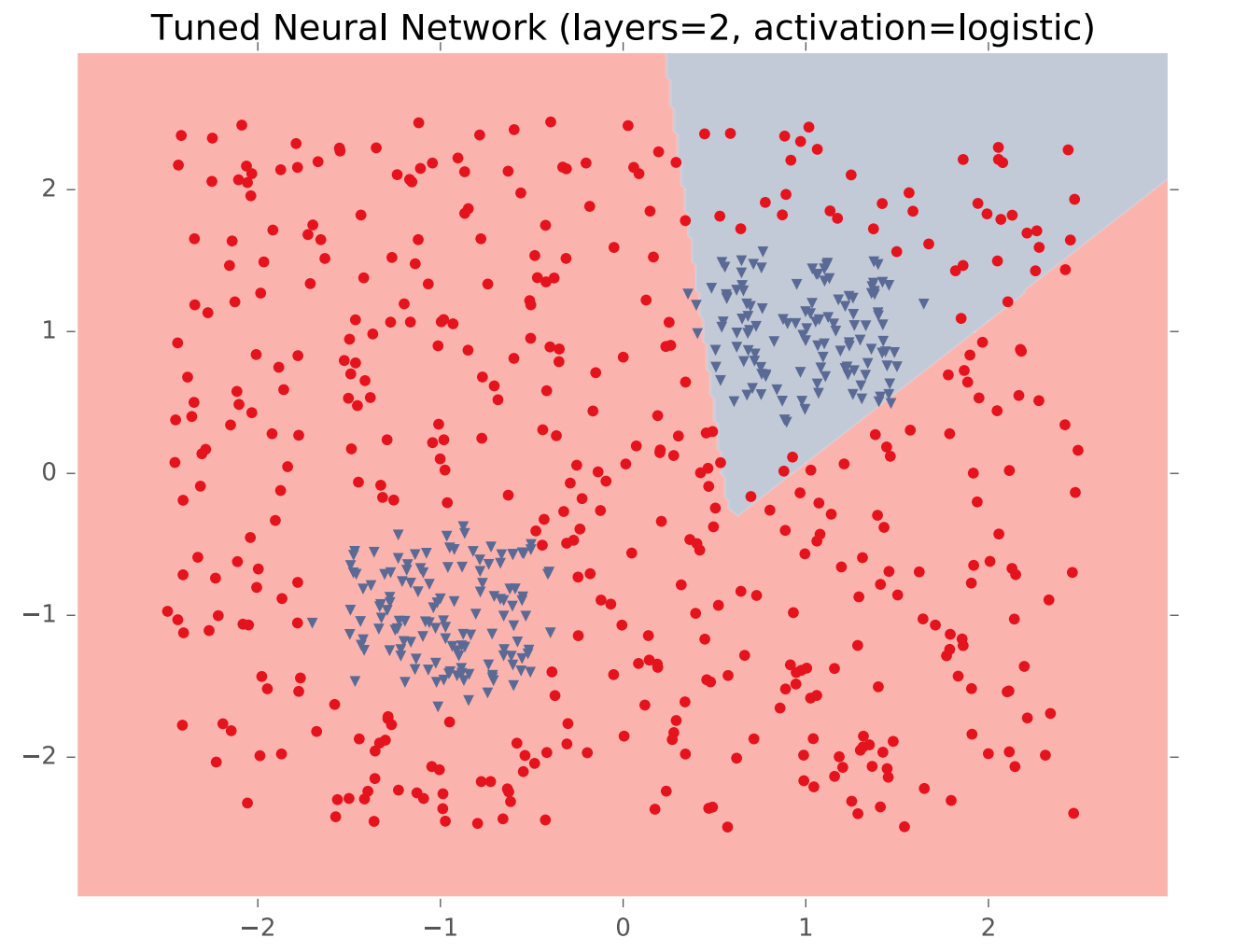
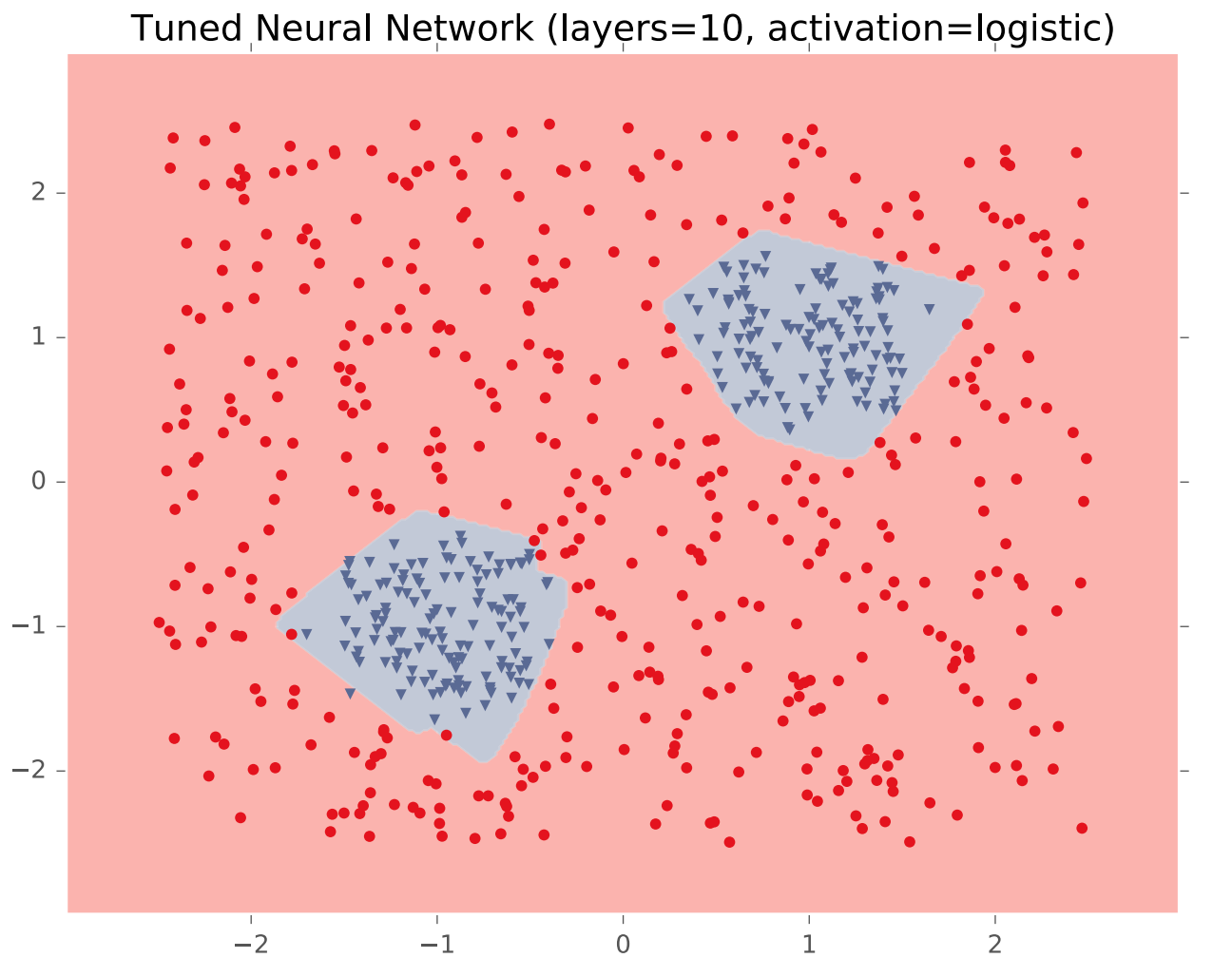
In theory, a single hidden layer is sufficient to approximate any continuous function, assuming you have enough hidden units. However, shallow networks may require very large numbers of hidden units. Deeper neural nets seem to be easier to design and train. Here's an example (from Matt Gormley) of a class boundary with a somewhat complex shape. K-nearest neighbor does a good job of approximating it (but is inefficient in higher dimensions).
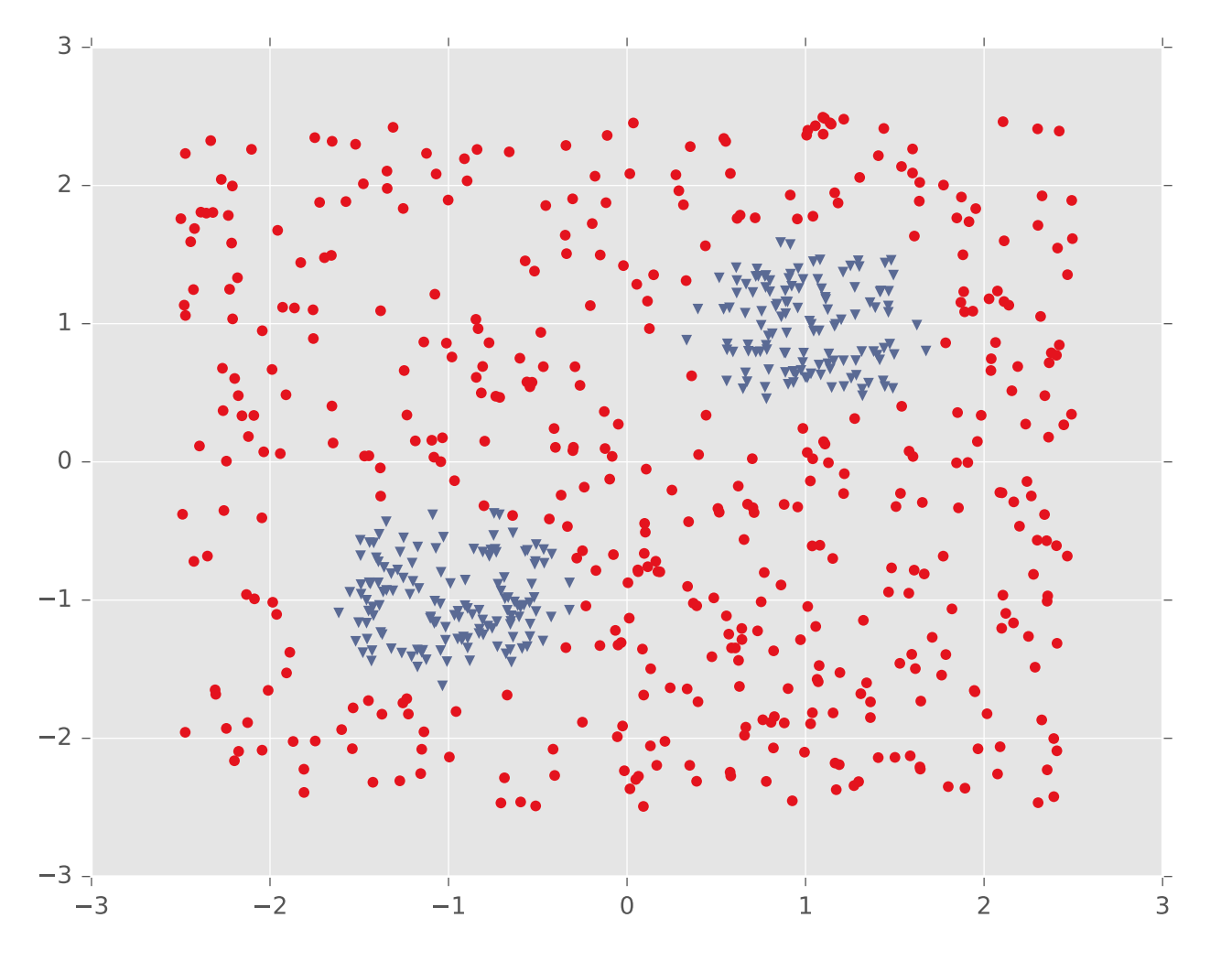
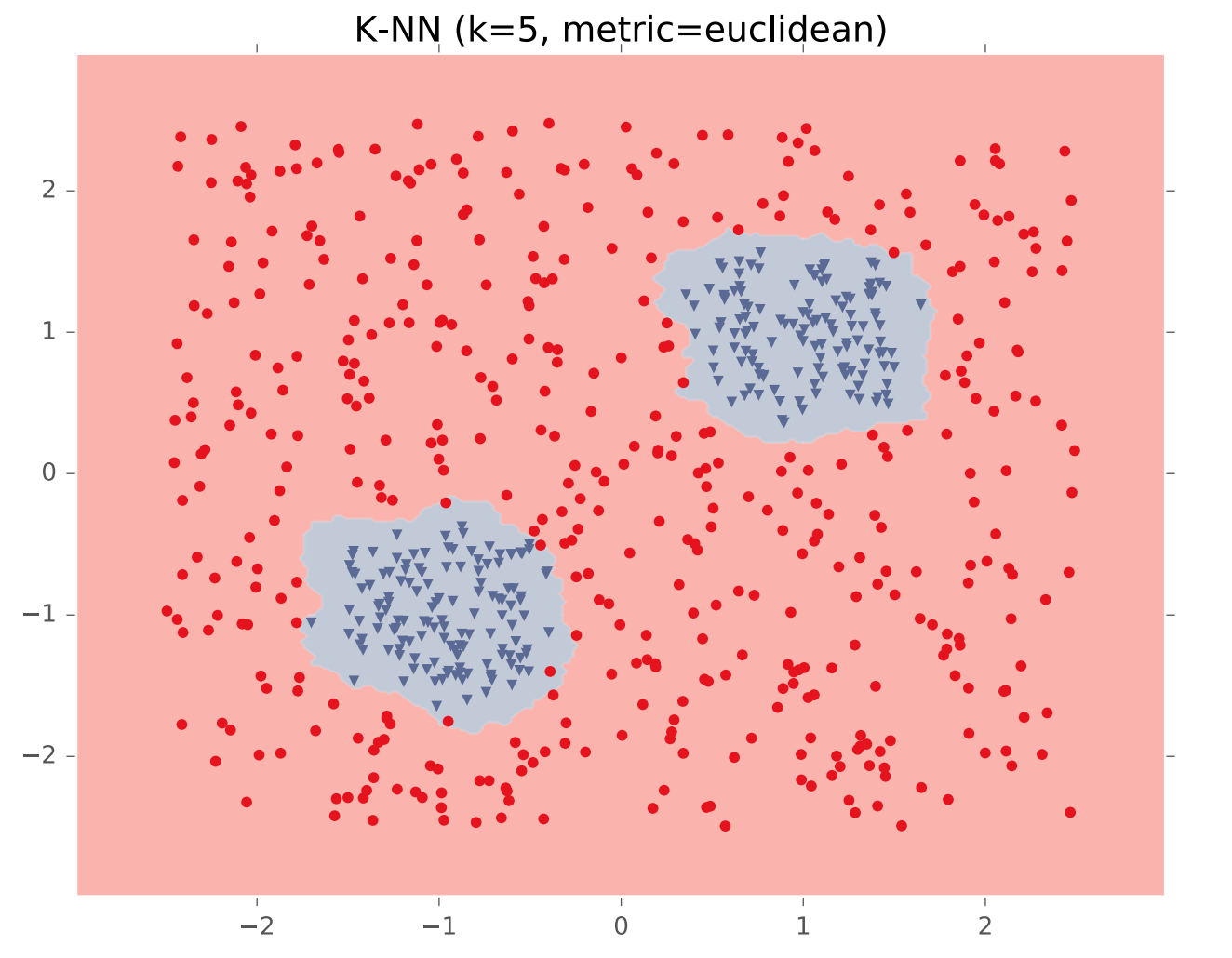
A two-layer network gives us a poor approximation (left), but a ten-layer network does a good job (right). Notice that our final network model is compact: proportional to the number of weights int the network. The size of k-nearest neighbor model grows with the number of training samples.
In image processing applications, deep networks normally emulate the layers of processing found in previous human-designed classifiers. So each layer transforms the input so as to make it more sophisticated ("high level"), compacts large inputs (e.g. huge pictures) into a more manageable set of features, etc. The picture below shows a face recognizer in which the bottom units detect edges, later units detect small pieces of the face (e.g. eyes), and the last level (before the output) finds faces.
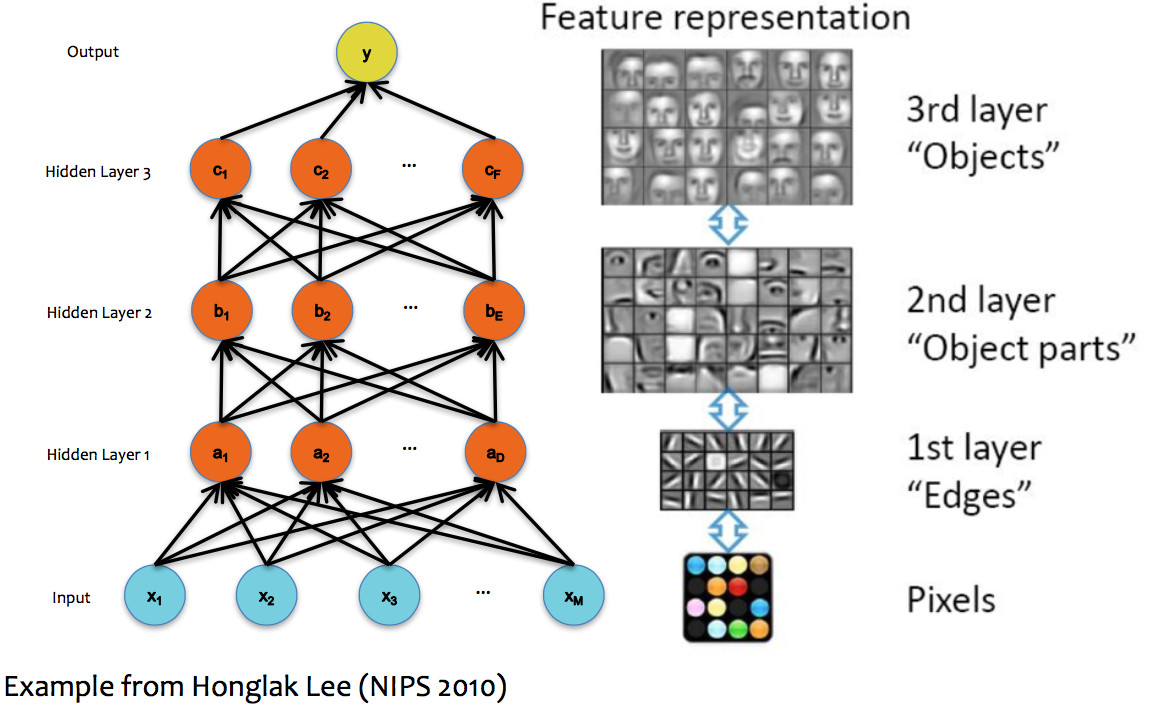
(from Matt Gormley)
Here are layers 1, 3, and 5 from a neural net trained on ImageNet (from M. Zeiler and R. Fergus Visualizing and Understanding Convolutional Networks).



Credits to Matt Gormley are from 10-601 CMU 2017