
a real-world trellis (supporting a passionfruit vine)
Suppose that W is our input word sequence (e.g. a sentence) and T is an input tag sequence. That is
\(W = w_1, w_2, \ldots w_n \)
\(T = t_1, t_2, \ldots t_n \)
Our goal is to find a tag sequence T that maximizes P(T | W). Using Bayes rule, this is equivalent to maximizing \( P(W \mid T) * P(T)/P(W) \) And this is equivalent to maximizing \( P(W \mid T) * P(T) \) because P(W) doesn't depend on T.
So we need to estimate P(W | T) and P(T) for one fixed word sequence W but for all choices for the tag sequenceT.
Obviously we can't directly measure the probability of an entire sentence given a similarly long tag sequence. Using (say) the Brown corpus, we can get reasonable estimates for
If we have enough tagged data, we can also estimate tag trigrams. Tagged data is hard to get in quantity, because human intervention is needed for checking and correction.
To simplify the problem, we make "Markov assumptions." A Markov assumption is that the value of interest depends only on a short window of context. For example, we might assume that the probability of the next word depends only on the two previous words. You'll often see "Markov assumption" defined to allow only a single item of context. However, short finite contexts can easily be simulated using one-item contexts.
For POS tagging, we make two Markov assumptions. For each position k:
\(P(w_k)\) depends only on \(P(t_k)\)
\(P(t_k) \) depends only on \(P(t_{k-1}) \)
Therefore
\( P(W \mid T) = \prod_{i=1}^n P(w_i \mid t_i)\)
\( P(T) = P(t_1 | START) * \prod_{i=1}^n P(t_k \mid t_{k-1}) \)
where \( P(t_1 | START) \) is the probability of tag \(t_1\) at the start of a sentence.
Folding this all together, we're finding the T that maximizes
\( P (T \mid W)\)
\(\propto P(W \mid T) * P(T) \)
\( = \prod_{i=1}^n P(w_i \mid t_i)\ \ * \ \ P(t_1 \mid \text{START})\ \ *\ \ \prod_{k=2}^n P(t_k \mid t_{k-1}) \)
Like Bayes nets, HMMs are a type of graphical model and so we can use similar pictures to visualize the statistical dependencies:
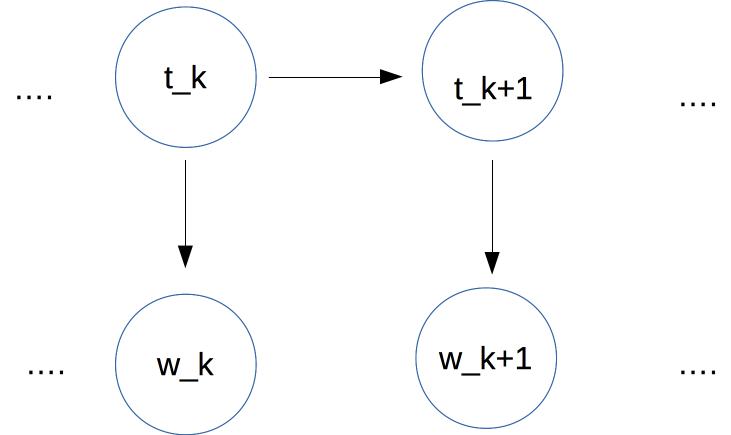
In this case, we have a sequence of tags at the top. Each tag depends only on the previous tag. Each word (bottom row) depends only on the corresonding tag.