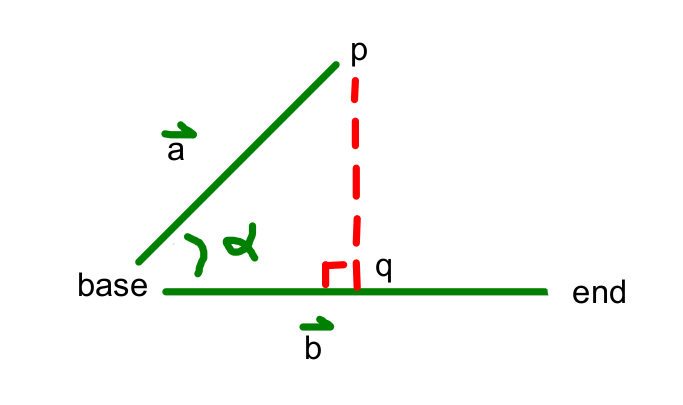
This picture shows a situation from MP 2. Vector \(\vec{b}\) goes from the base of a robot arm's link to the end of the link. Vector \(\vec{a}\) goes from the base to some other point p. Both vectors live in 2D and could point in any direction. We'll see some similar situations in higher dimensions when we get to vector semantics.
We've dropped a perpendicular from p to the line containing \(\vec{b}\), intersecting the line at point q. Depending on the problem, we'd like the distance from p to q and/or the distance from the base to q. Let's think of these distances as signed, because that's often what you need. For example, the sign of the distance from the base to q tells you whether q on the correct side of the base to be in the line segment defined by base and end.
You'll recal from high school geometry that
However, we'd prefer not to convert to/from angles because those library functions tend to be slow. So, instead, you should exploit the following equations:
\(\vec{a} \cdot \vec{b} \) is the dot product. \(\vec{a} \times \vec{b} \) is sometimes called the "cross product" in 2D geometrical algorithms. More exactly, it is the sign and magnitude of the cross product for two vectors that live in the plane \(z=0\). More concretely, if \(\vec{a} = (a_1,a_2)\) and \(\vec{b} = (b_1,b_2)\), then
Now you have to do some algebra. So you'll need to substitute one equation into another. Also you'll often need to calculate \(|\vec{b}|\) so you can remove it from equations.
In higher dimensions, you can still use the dot product to compute cosine.
Here's one example of using a signed result. The vector \(\vec{b}\) defines a line L. The sign of sin(\(\alpha\)) tells you which side of this line p is on. If you have a line segment from p to another point, you can tell whether it crosses L by testing whether this sign changes between the two endpoints.