A stochastic game is one in which some changes in game state are random, e.g. dice rolls, card games. That is to say, most board and card games. These can be modelled using game trees with three types of nodes
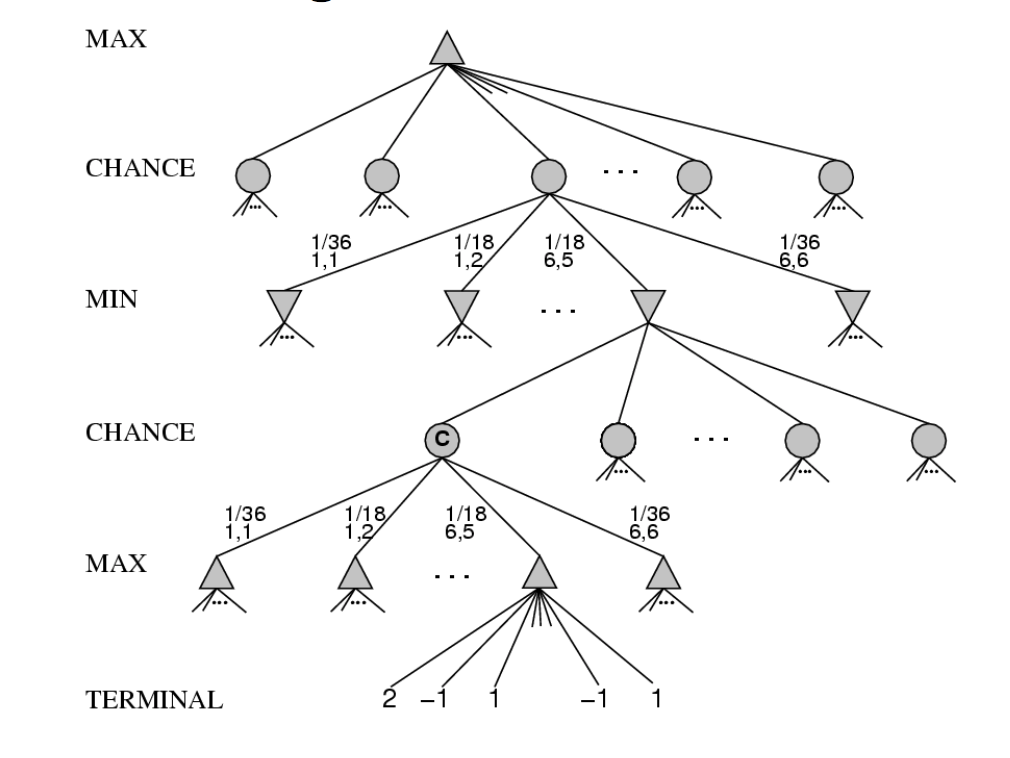
from Russell and Norvig
Expectiminimax is an extension of minimax for propagating values upwards in trees with chance nodes. Min and max nodes work as normally. For chance nodes, node value is the expected value over all its children.
That is, suppose the possible outcomes of a random action are \(s_1, s_2, ..., s_n\). Put each outcome in its own child node. Then the value for the parent node will be \( \sum_k P(s_k)v(s_k) \). The toy example below shows how this works:
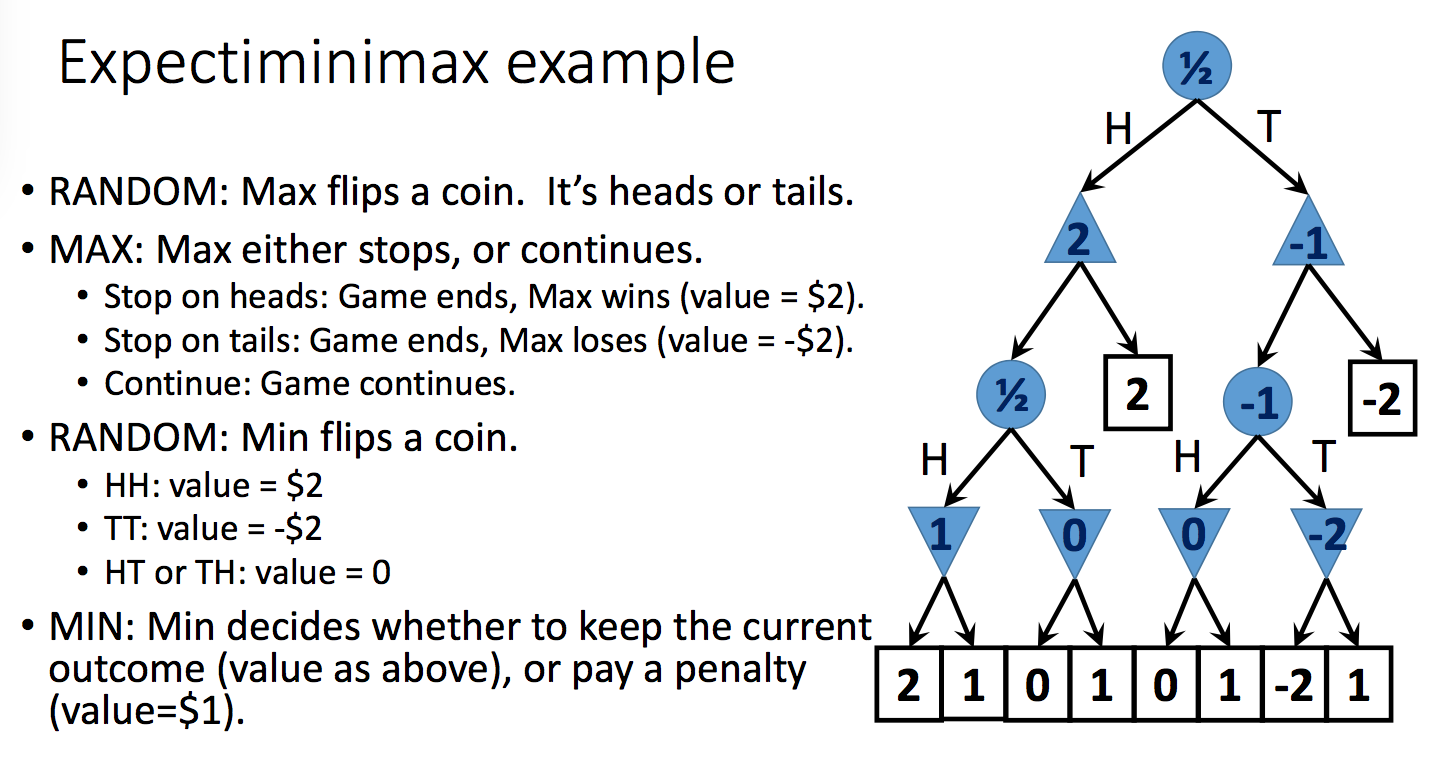from Lana Lazebnik
This all works in theory. However, chance nodes add enough level to the tree and, in some cases (e.g. card games), they can have a high branching factor. So games involving random section (e.g. poker) can quickly become hard to solve by direct search.
A related concept is imperfect information. In a game with imperfect information, there are parts of the game state that you can't observe, e.g. what's in the other player's hand. Again, typical of many common board and card games. We can also draw these as chance nodes, as in the example below (from Lana Lazebnik). Notice that Lincoln's face is on the penny and Jefferson's face is on the nickel.
One way to model such a situation is to say that the agent is in one of several states:
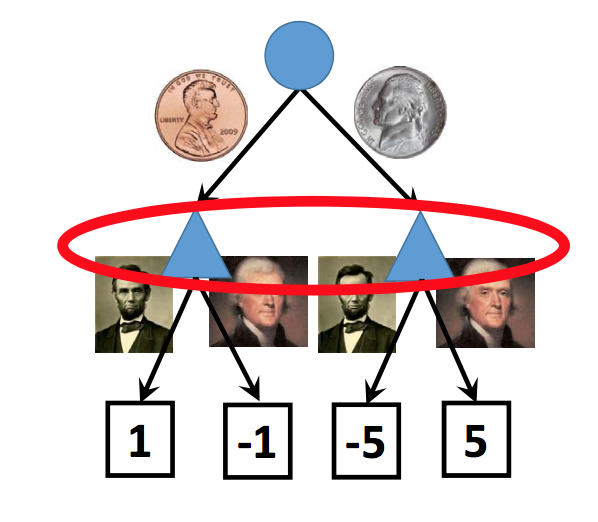
In broad outline, this is similar to the standard trick in automata theory for modelling an NFA using a DFA whose states are sets of NFA states. The game playing program would then pick a common policy that will work for the whole set of possible states. For example, if you're playing once and can't afford to lose, you might pick the policy that minimizes your loss in the worst case. In the example above, this approach would pick Jefferson.
In a more complex situation, the group of states might share common features that could be leveraged to make a good decision. For example, suppose you are driving in a city and have gotten lost. You stop to ask for directions because you "have no idea" where you are. Actually, you probably do have some idea. If you're lost in Chicago, you'd ask for directions in English. In Beijing, you'd do this in Chinese. Your group of alternative states shares a common geographic feature. This can be true for complex game states, e.g. you don't know their exact hand but it apparently contains some diamonds.
Alternatively, we could restructure the representation so that we have a stochastic chance node after our move, as in this picture:
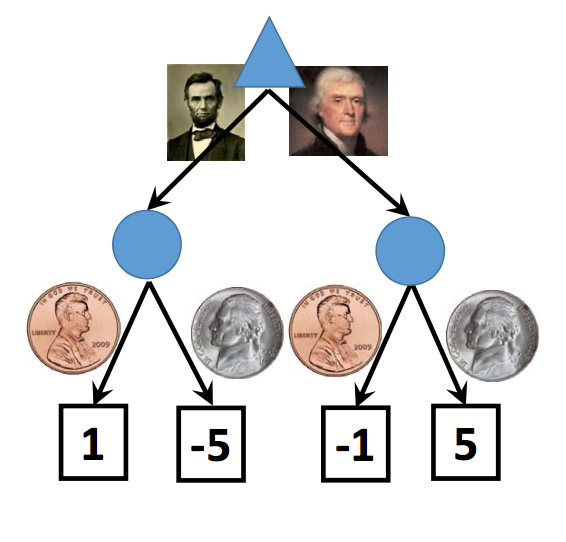
This is a good approach if you are playing the game repeatedly and have some theory of how likely the two coins are. If the two coins are equally likely, the corresponding expectiminimax analysis would compute the expected value for each of the two chance nodes (-2 for the left one, 2 for the right one). This again leads to a choice of Jefferson. However, in this case, the best choice will change depending on our theory of how likely the two types of coins are.
But what if our opponent is thinking ahead? How often would she actually choose to pick the penny vs. the nickel? Or, if she's picking randomly from a bag of coins, what percentage of the coins are really pennies?
>>> Question for the reader: what probability of penny vs. nickel would be required to change our best choice to Lincoln?
Game trees involving chance nodes can quickly become very large, restricting exhaustive search to a small lookahead in terms of mvoes. One method for getting the most out of limited search time is to randomly select trees. That is
This method limits to the correct node values as n gets large. In practice, we make n as large as resources allow and live with the resulting approximation error.
A similar approach can be used on deterministic games where the trees are too large for other reasons. That is
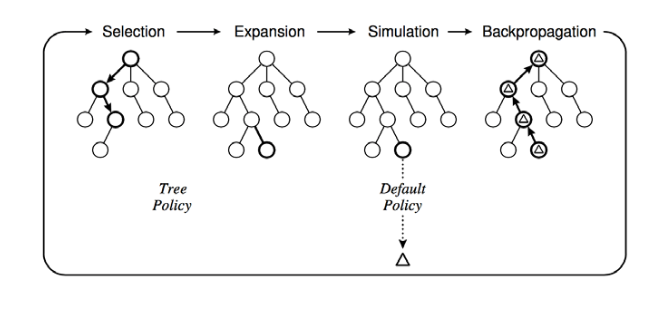
from C. Browne et al., A survey of Monte Carlo Tree Search Methods, 2012
Poker is a good example of a game with both a chance component and incomplete information. It is only recently that poker programs are competitive. CMU's Libratus system recently (2017) beat some of the best human players ( geekwire, CMU news).
Libratus uses three modules to handle three key tasks:
It used a vast amount of computing power: 600 of the 846 compute nodes in the "Bridges" supercomputer center. Based on the news articles, this would have 1 pentaflop, i.e. 5147 times as much processing power as a high-end laptop. And the memory was 195 Terabyes, i.e. 12,425 times as much as a high-end laptop. This is a good example of current state-of-the-art game programs requiring excessive amounts of computing resources, because game performance is so closely tied to the raw amount of search that can be done. However, improvements in hardware have moved many AI systems from a similar niche to eventual installation on everyday devices.
For a more theoretical (probably completmentary) approach, check out the CFR* Poker algorithm.
Another very recent development are programs that play Go extremely well. AlphaGo and its successor AlphaZero combine Monte Carlo tree search with neural networks that evaluate the goodness of board positions and estimate the probability of different choices of move. In 2016, AlphaGo beat Lee Se-dol, believed to be the top human player at the time. More recent versions work better and seem to be consistently capable of beating human players.
More details can be found in
In a recent news article, the BBC reported that Lee Se-dol quit because AI "cannot be defeated."