from Berkeley CS 188 slides
Each tree node represents a game state. As imagined by a theoretician, we might use the following bottom-up approach to finding our best move:
As we'll see soon, we can often avoid building out the entire game tree (even to depth d). So a better approach to implementation uses recursive depth-first search. So the algorithm for finding our best move actually looks like:
How do we make this process more effective?
Idea: we can often compute the utility of the root without examining all the nodes in the game tree.
Once we've seen some of the lefthand children of a node, this gives us a preliminary value for that node. For a max node, this is a lower bound on the value at the node. For a min node, this gives us an upper bound. Therefore, as we start to look at additional children, we can abandon the exploration once it becomes clear that the new child can't beat the value that we're currently holding.
Here's an example from from Diane Litman (U. Pitt).
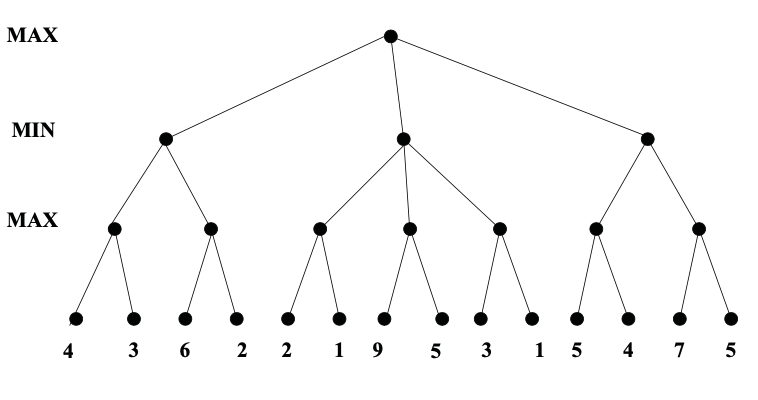
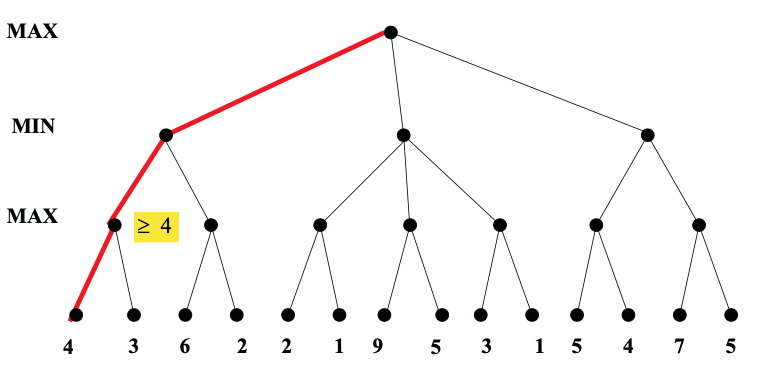
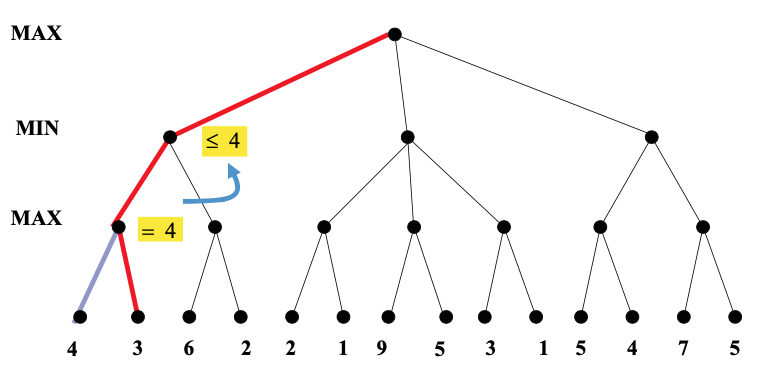
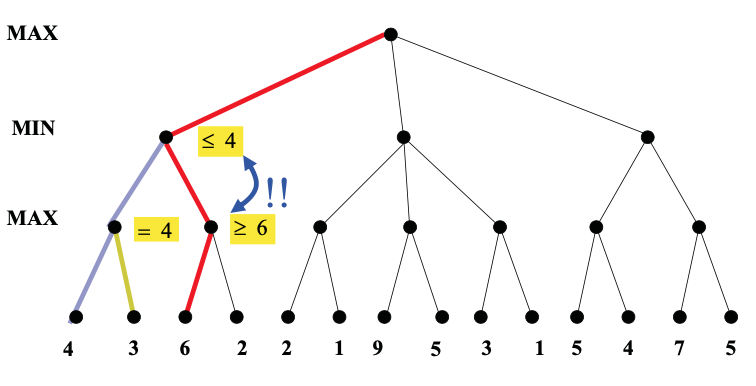
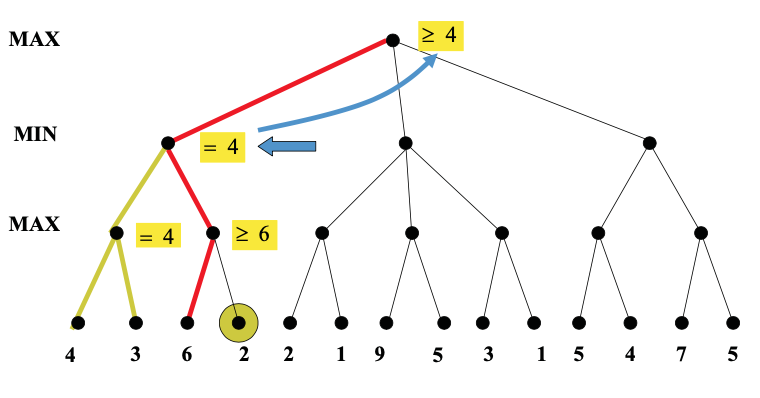
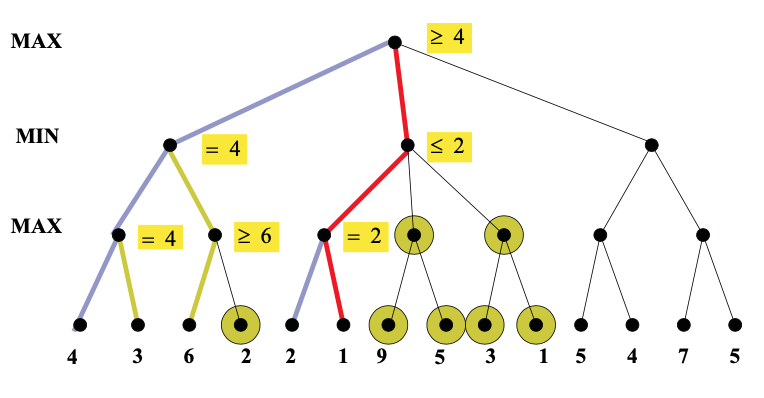
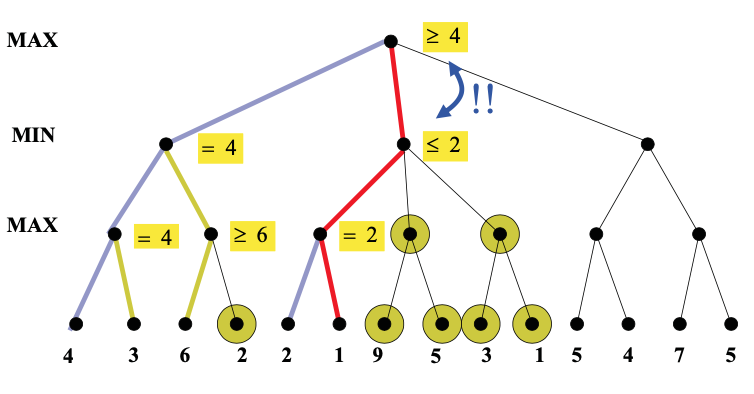
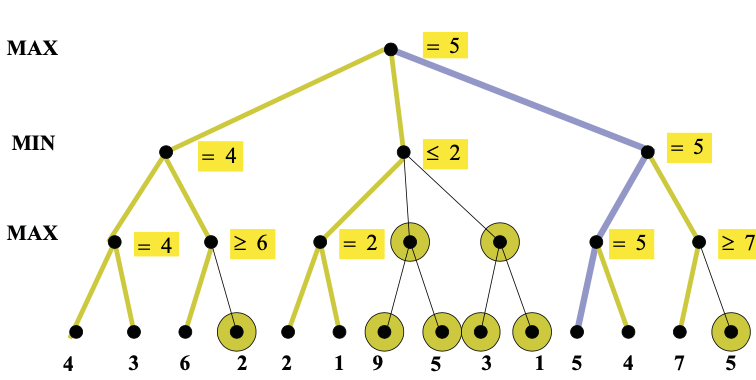
As you can see from this example, this strategy can greatly reduce the amount of the tree we have to explore. Remember that we're building the game tree dynamically as we do depth-first search, so "don't have to explore" means that we never even allocate those nodes of the tree.
That the left-to-right order of nodes matters to the performance of alpha-beta pruning. Remember that the tree is built dynamically, so this left-to-right ordering is determined by the order in which we consider the various possible actions (moves in the game). So the node order is something we can potentially control.
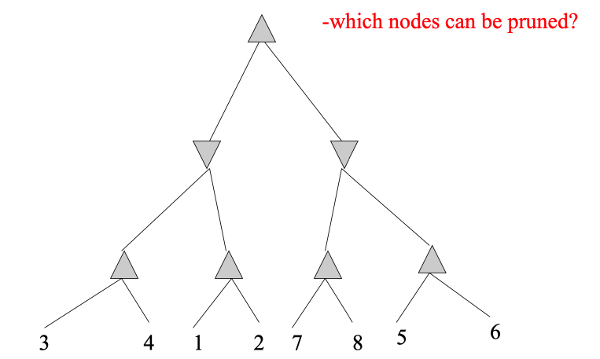
Consider this example (from Mitch Marcus (U. Penn), adapted from Rick Lathrop (USC)). None of these nodes can be pruned by alpha-beta, because the best values are always on the righthand branch.
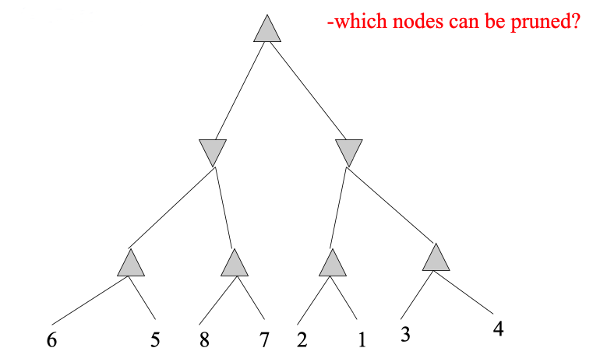
If we reverse the left-to-right order of the values, we can do considerable pruning:
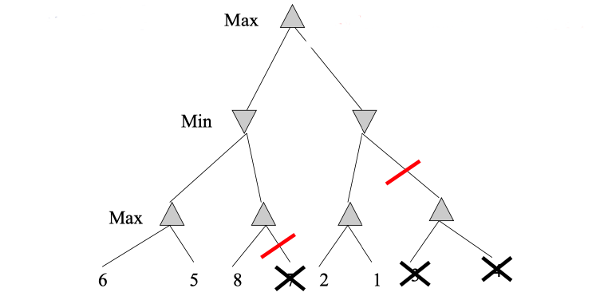
Suppose that we have b moves in each game state (i.e. branching factor b), and our tree has height m. Then standard minimax examines \(O(b^m) \) nodes. If we visit the nodes in the optimal order, alpha-beta pruning will reduce the number of nodes searched to \(O(b^{m/2}) \). If we visit the nodes in random order, we'll examine \(O(b^{3m/4}) \) on average.
Obviously, we can't magically arrange to have the nodes in exactly the right order, because the whole point of this search is to find out what values we have at the bottom. However, heuristic ordering of actions can get close to the optimal \(O(b^{m/2})\) in practice. For example, a good heuristic order for chess examines possible moves in the following order: