Game search differs in several ways from the types of search we've seen so far.
For example, chess has about 35 moves from any board configuration. A game may be 100 ply deep. So the full search tree will contain about 35^100 nodes which is about 10^154 nodes.
→ What is a "ply"? This is game computing jargon for one turn by one player. A "move" is a sequence of plies in which each player has one turn. This terminology is consistent with common usage for some, but not all, games.
The large space of possibilities makes games difficult for people, so performance is often seen as a measure of intelligence. In the early days, games were seen as a good domain for computers to demonstrate intelligence. However, it has become clear that the precise definitions of games make them comparatively easy to implement on computers. AI has moved more towards practical tasks (e.g. cooking) as measures of how well machines can model humans.
Game performance is heavily dependent on search and, therefore, high-performance hardware. Scrabble programs beat humans even back in the 1980's. More games have become doable. The graph below shows how computer performance on chess has improved gradually, so that the best chess and go programs now beat humans. High-end game systems have become a way for computer companies to show off their ability to construct an impressive array of hardware.
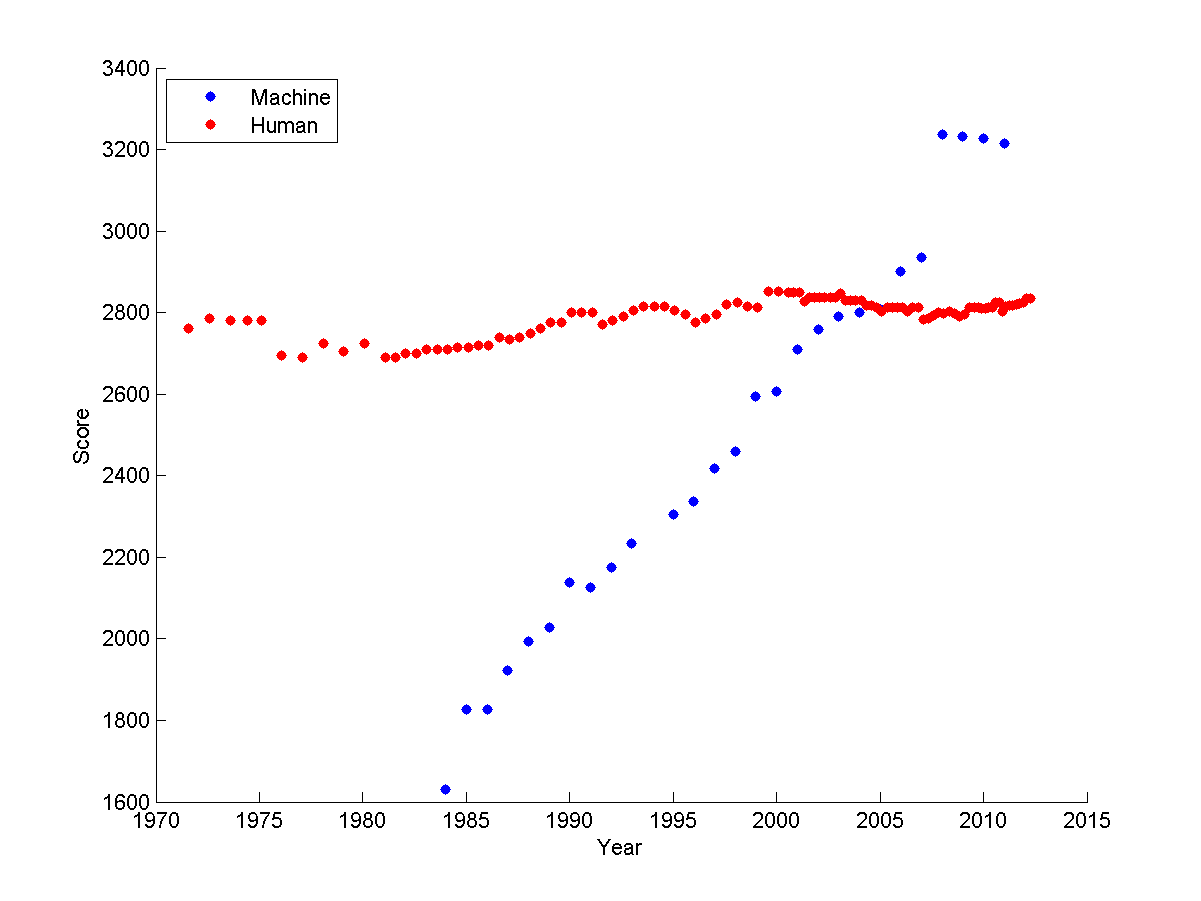
chess Elo ratings over time
from
Sarah Constantin
Games come in a wide range of types. The most basic questions that affect the choice of computer algorithm are:
| fully observable? | determininistic? | size | |
|---|---|---|---|
| Tic-tac-toe | yes | yes | small |
| Chess | yes | yes | big |
| Monopoly | yes | no | big |
| Poker | no | no | big |
Some other important properties:
What is zero sum? Final rewards for the two (or more) players sum to a constant. That is, a gain for one player involves equivalent losses for the other player(s) This would be true for games where there are a fixed number of prizes to accumulate, but not for games such as scrabble where the total score rises with the skill of both players.
Normally we assume that the opponent is going to play optimally, so we're planning for the worst case. Even if the opponent doesn't play optimally, this is the best approach when you have no model of the mistakes they will make. If you do happen to have insight into the limitations of their play, those can be modelled and exploited.
Time limits are most obvious for competitive games. However, even in a friendly game, your opponent will get bored and walk away (or turn off your power!) if you take too long to decide on a move.
Many video games are good examples of dyanmic environments. If the changes are fast, we might need to switch from game search to methods like reinforcement learning, which can deliver a fast (but less accurate) reaction.
We'll normally assume zero sum, two players, static, large (but not infinite) time limit. We'll start with deterministic games and then consider stochastic ones.
Games are typically represented using a tree. Here's an example (from Mitch Marcus at U. Penn) of a very simple game called Hexapawn, invented by Martin Gardner in 1962.

This game uses the two pawn moves from chess (move forwards into an empty square or move diagonally to take an opposing piece). A player wins if (a) he gets a pawn onto the far side, (b) his opponent is out of pawns, or (c) his opponent can't move.
The top of the game tree looks as follows. Notice that each layer of the tree is a ply, so the active player changes between successive levels.
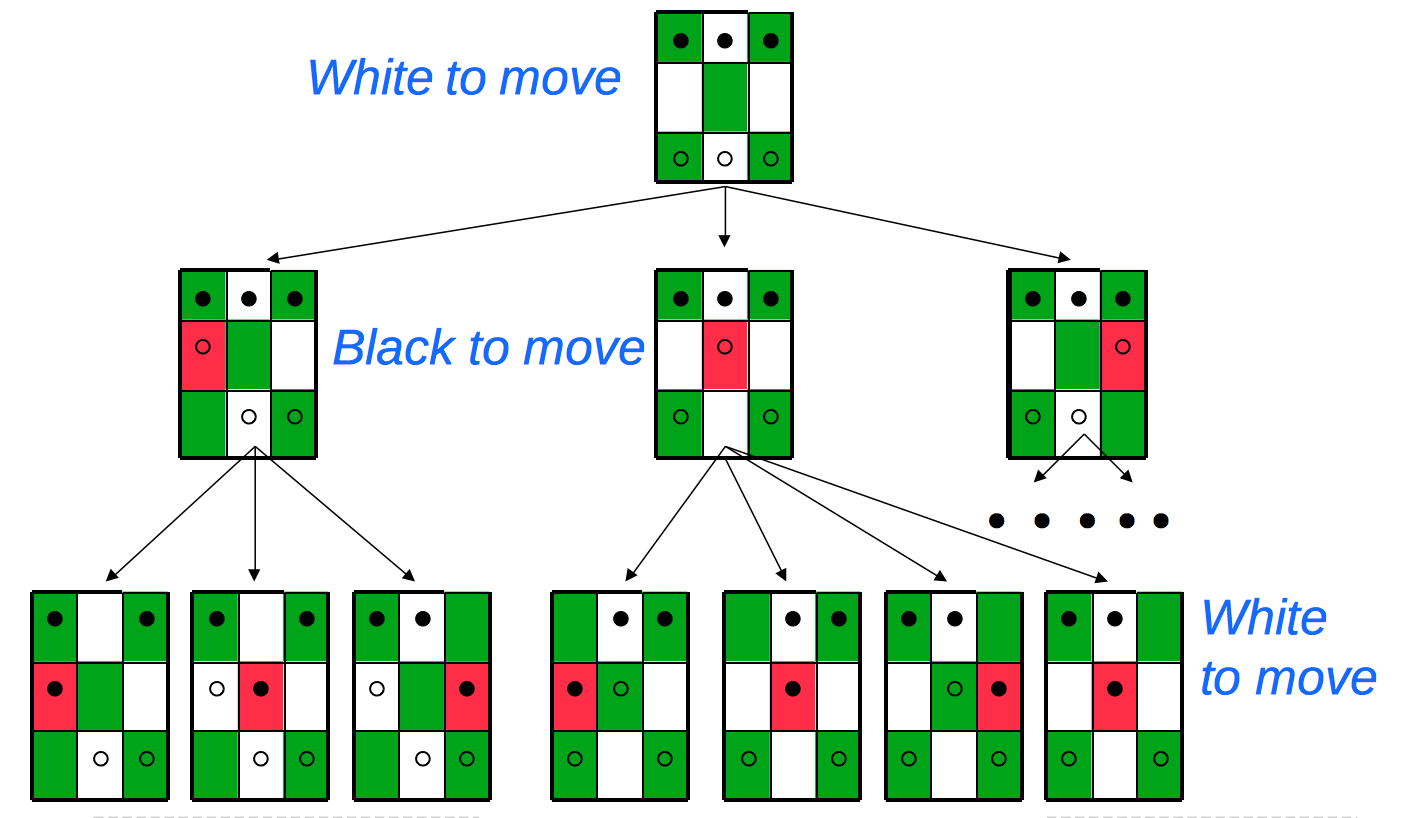
Notice that a game "tree" may contain nodes with identical contents. So we might actually want to treat it as a graph. Or, if we stick to the tree represenation, memoize results to avoid duplicating effort.
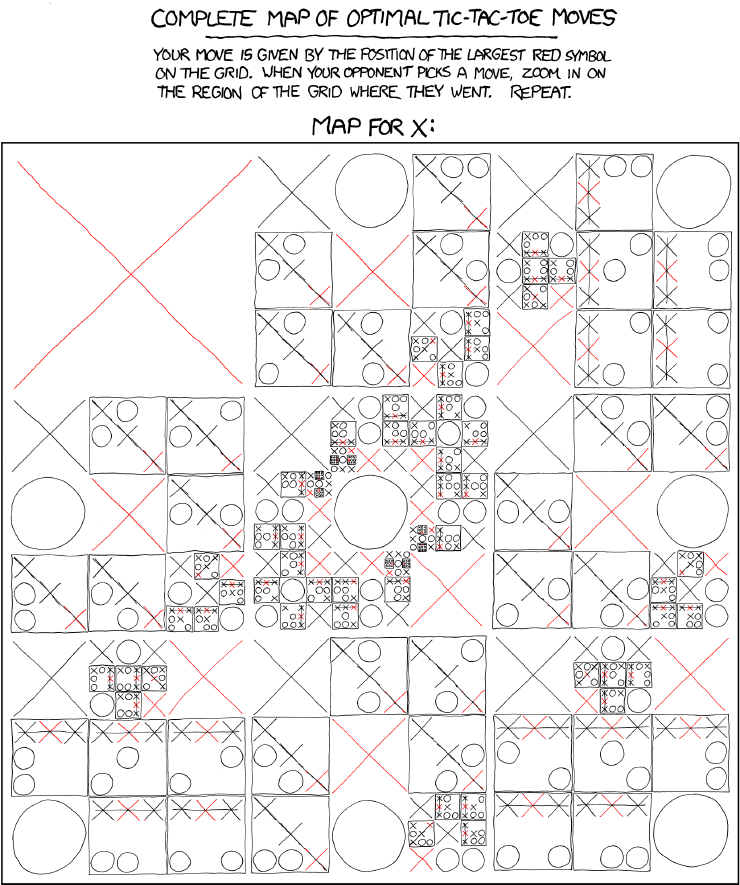
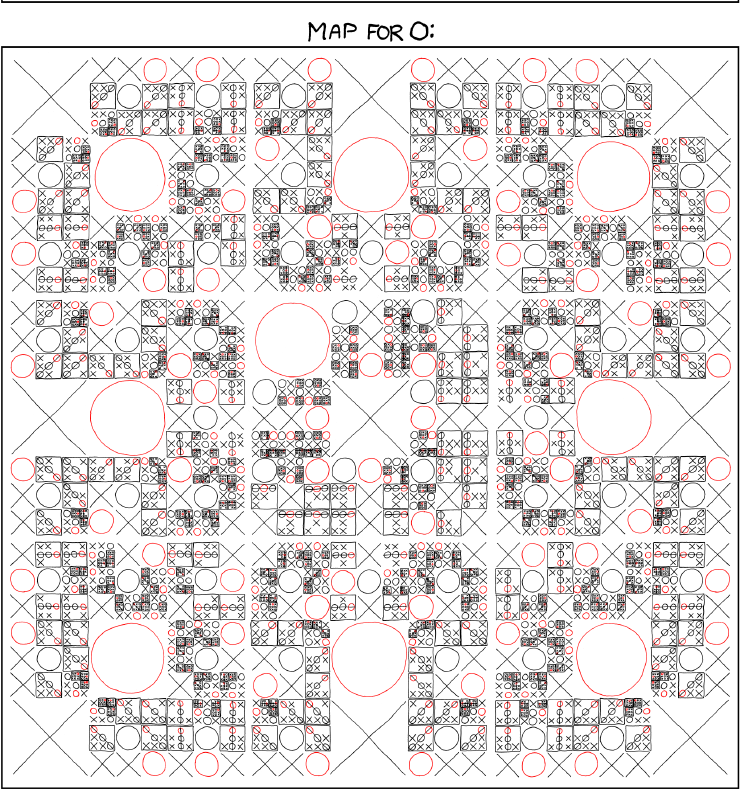
Here's the start of the game tree for a more complex game, tic-tac-toe.
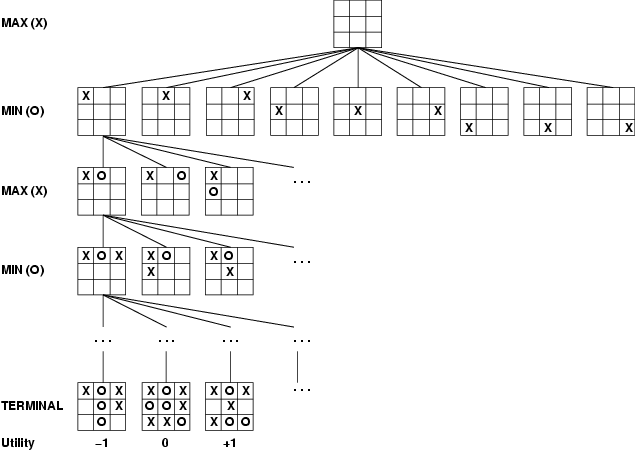
Tic-tac-toe is still simple enough that we can expand out the entire tree of possible moves. It's slightly difficult for humans to do this without making mistakes, but computers are good at this kind of bookkeeping. Here's the details, compacted into a convenient diagram by the good folks at xkcd: