There are two basic approaches to solving constraint satisfaction problems: hill climbing and backtracking search. CSP problems may include multi-variate constraints. E.g. sudoku requires that there be no duplicate values within each row/column/block. For this class, we'll stick to constraints involving two variables.
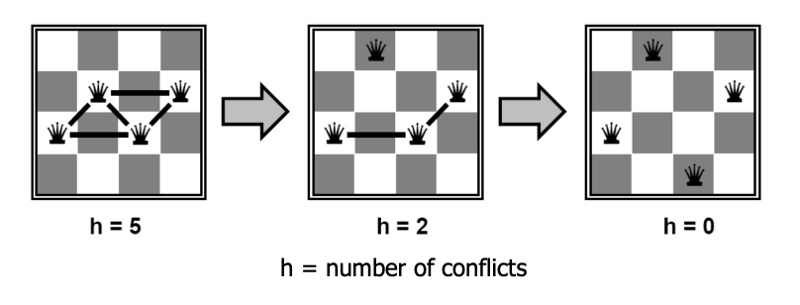
In the hill-climbing approach, we randomly pick a full set of variable assignments, then try to tweak it into a legal solution. At each step, our draft solution will have some constraints that are still violated. We change the value of one variable to try to reduce the number of conflicts as much as possible. (If there are several options, pick one randomly.) In the following example, this strategy works well:
from Lana Lazebnik, Fall 2017
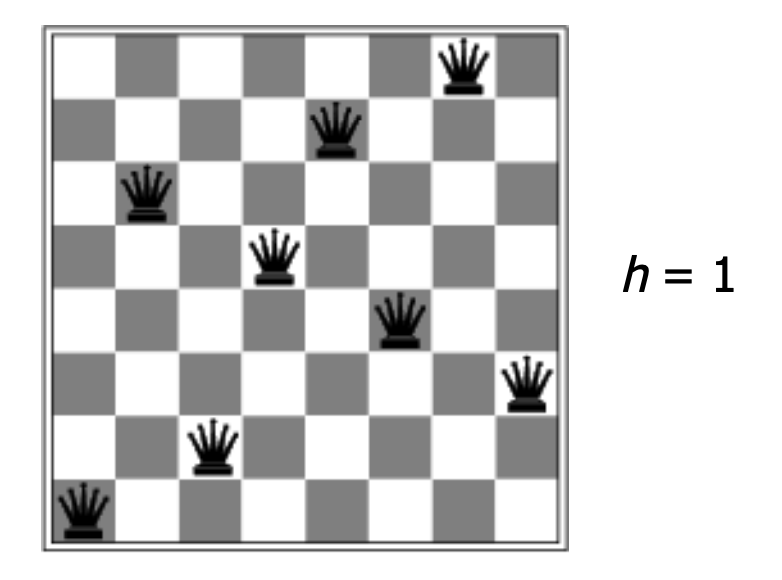
Hill climbing can be very effective on certain problems, and people frequently use it to solve complicated constraint satisfaction problems, e.g. scheduling classes or final exams. However, this method can get stuck in local optima. For example, the following configuration for 8 Queens has a single constraint violation, but no adjustment of a single piece will reduce the number of violations to zero.
from Lana Lazebnik, Fall 2017
To avoid being stuck in local optima, hill-climbing algorithms often add some randomization:
The other basic approach to a constraint satisfaction problem is to choose variable values one at a time, undoing assignments ("backtracking") when we discover that our current set of assignments can't work. Specifically, we set up search as follows:
CSP search has some special properties which will affect our choice of search method. If our problem has n variables, then all solutions are n steps away. So DFS is a good choice for our search algorithm.
We can use a very stripped down DFS implementation, without explicit loop detection. This can be made to use only a very small amount of memory. In this type of AI context, DFS is often called "backtracking search" because it spends much of its time getting blocked and retreating back up the search tree to try other options.
A variety of heuristics can be used to speed up backtracking search. Let's start by looking at when to detect that our path is failing and we need to backtrack.
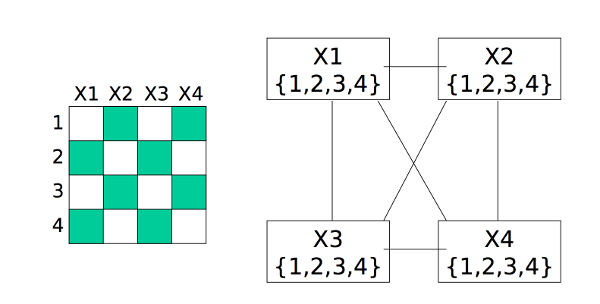
Here is a little demo of forward checking, from Bonnie Dorr, U. Maryland, via Mitch Marcus at U. Penn. We start with each variable x having a full list of possible values D(x) and no assignments.
First, we assign a value to the first variable. The purple cells show which other assignments are now problematic.
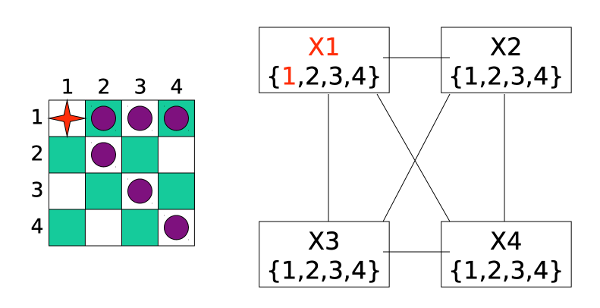
Forward checking now removes conflicting values from each list D(x).
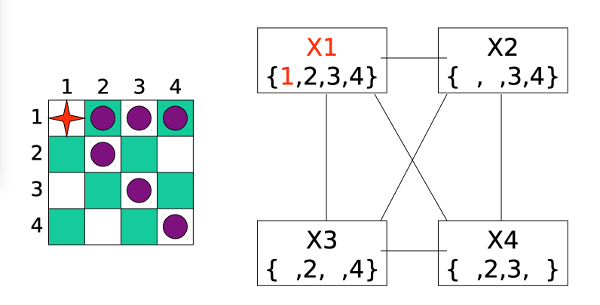
We now pick a value for our second variable.
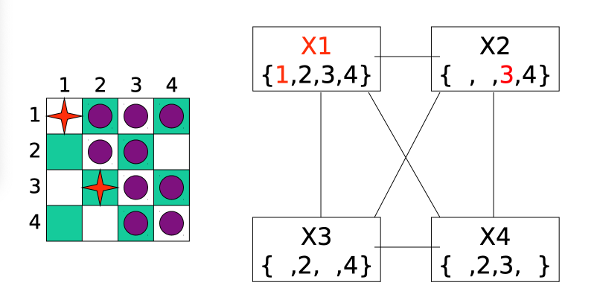
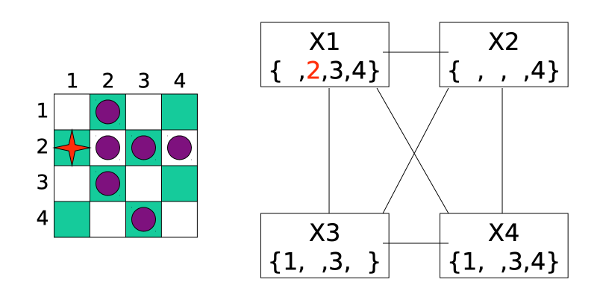
However, when we do forward checking, we discover that variable X3 has no possible values left. So we have to backtrack and undo the most recent assignment (to X2).
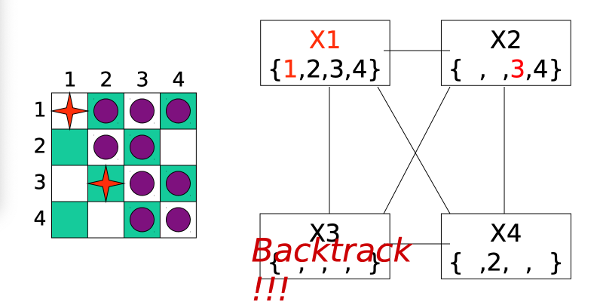
After some more assignments and backtracking, we end up giving up on X1=1 and moving on to exploring X1=2.
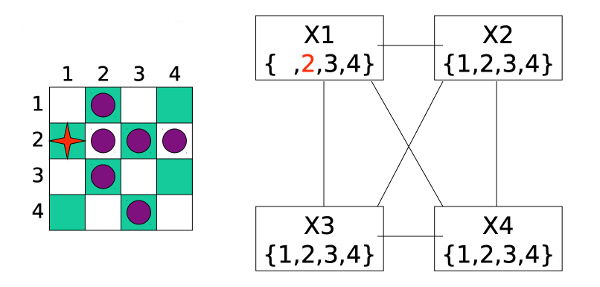
Forward checking reduces the sets of possible values to this:
After a few more steps of assignments and forward checking, we reach a full solution to the problem:
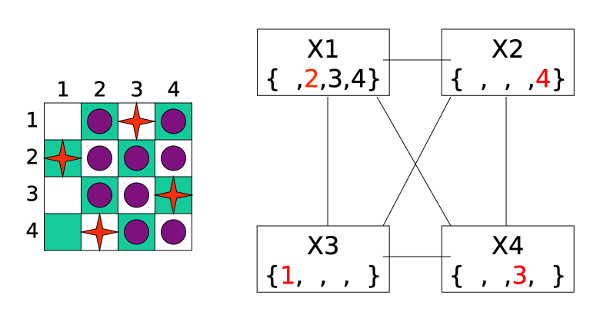
In the previous example, we tried variables in numerical order, i.e. how they came to us in the problem statement. When solving more complex problems, it can be important to use a smarter selection method. For example:
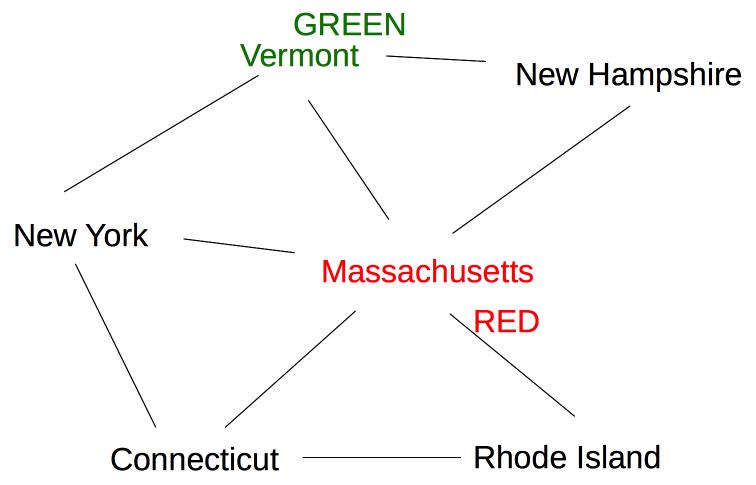
Suppose we are coloring the following graph with 3 colors (red, green, blue).
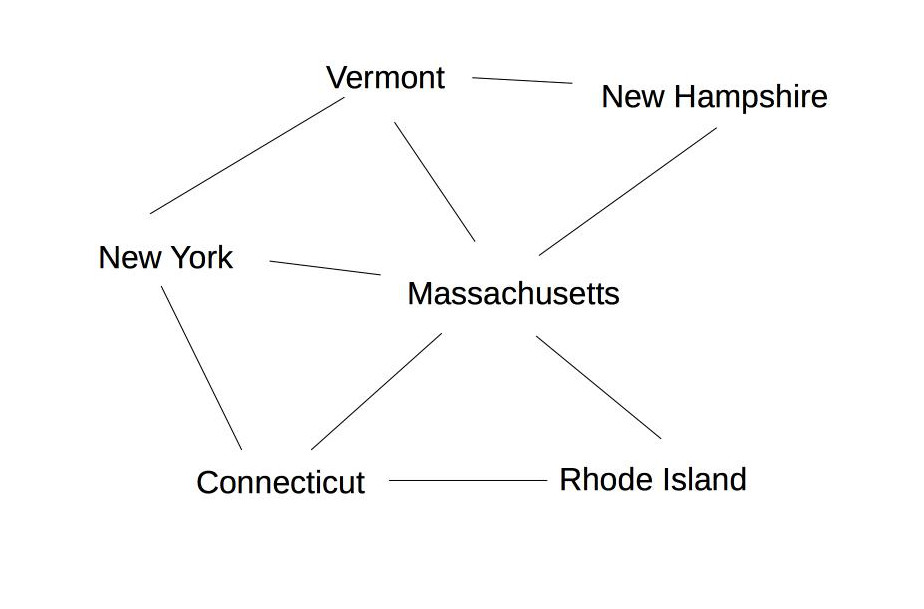
All states have three possible color values, so we use heuristic (b) and pick a color for Massachusetts:
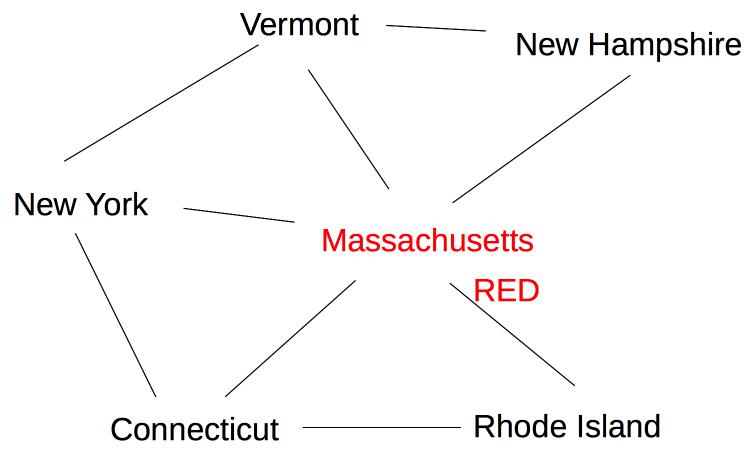
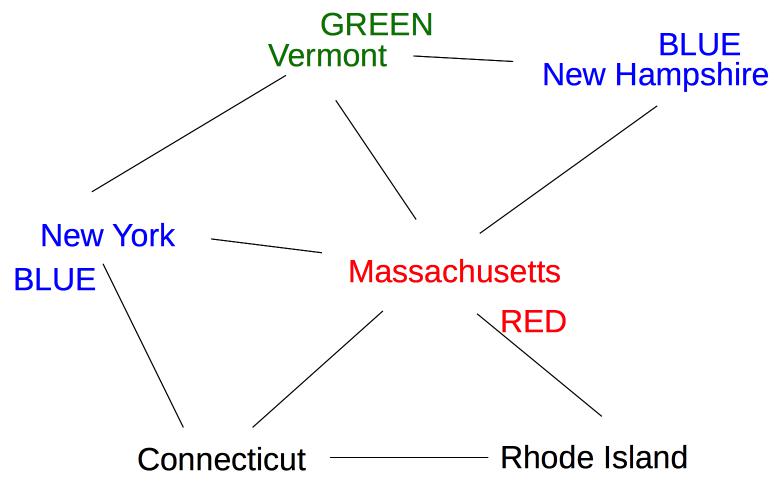
The five remaining states are still tied on (a), so we use heuristic (b) to pick one of the states with three neighbors (Vermont):
Now two states (New York and New Hampshire) have only one possible color value (blue), so we color one of them next:
Once we've chosen a variable, we can be smart about the order in which we explore its values. A good heuristic is:
For example, suppose we're trying to pick a value for the lower left node in the graph below. We should try Green first, because it leaves two color options open for the lower right node.
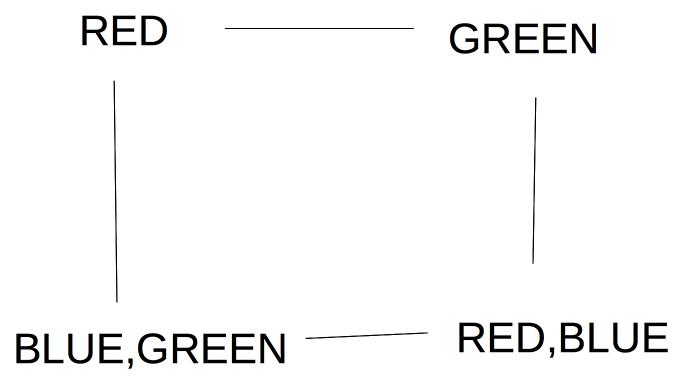
If this preferred choice doesn't work out, then we'll back up and try the other choice (Blue).
Constraint solving code should be designed to exploit any internal symmetries in the problem. For example, the map coloring problem doesn't care which color is which. So it doesn't matter which value we pick for the first variable (sometimes also some later choices). Similarly, there aren't really four distinct choices for the first column of n-queens, because reflecting the board vertically (or horizontally) doesn't change the essential form of the solution.