The last few topics in this course cover specialized types of search. These were once major components of AI systems. They are are still worth knowing about because they still appear in the higher-level (more symbolic) parts of AI systems. We'll start by looking at constraint satisfaction problems.
Remember that a queen in chess threatens another piece if there is a direct path between the two either horizontally, or vertically, or diagonally. In the n queens problem, we have to place n queens on a n by n board so that no queen threatens another. Here is a solution for n=8:

From Wikipedia
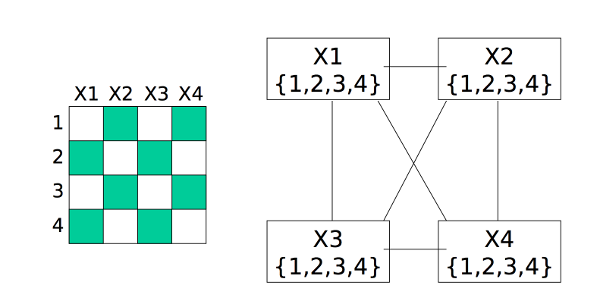
Since each column must contain exactly one queen, we can model this as follows
We can visualize this as a graph in which each variable is a node and edges link variables involved in binary constraints. So X1 in the following diagram is a variable representing a column. Its possible values {1,2,3,4} are the row to place the queen in.
from Bonnie
Dorr, U. Maryland
(via Mitch Marcus at U. Penn).
A constraint-satisfaction problem (CSP) consists of
In many examples, all variables have the same set of allowed values. But there are problems where different variables may have different possible values.
Need to find a complete assignment (one value for each variable) that satisfies all the constraints
In basic search problems, we are explicitly given a goal (or perhaps a small set of goals) and need to find a path to it. In a constraint-satisfaction problem, we're given only a description of what constraints a goal state must satisfy. Our problem is to find a goal state that satisfies these constraints. We do end up finding a path to this goal, but the path is only temporary scaffolding.
From
Wikipedia
Viewed as a CSP problem
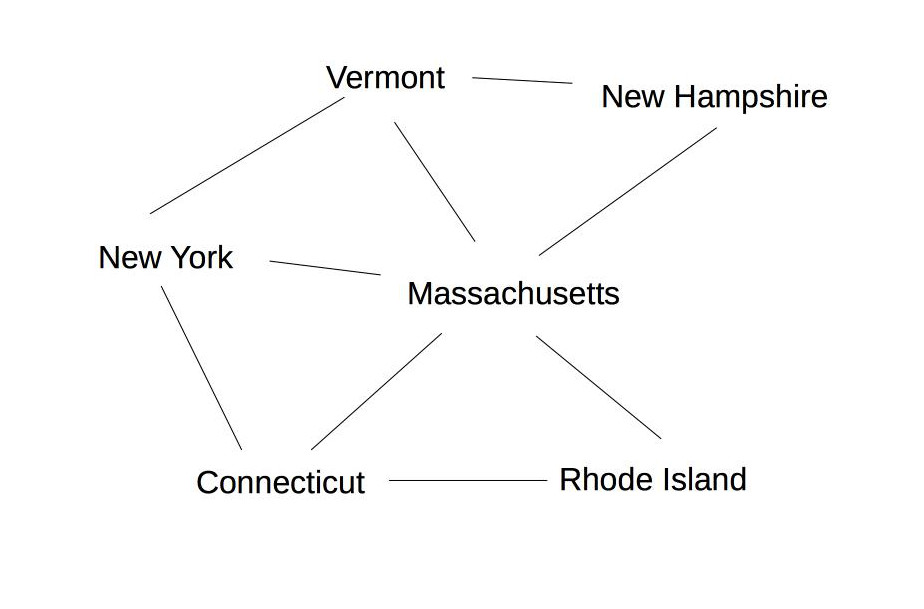
Pictured as a constraint graph, the states/countries are nodes, and edges connect adjacent states. A small example is shown below. Theoretical work on this topic is found mostly under the keyword "graph coloring." Applications of graph coloring include register allocation, final exam scheduling.
The "4 color Theorem" states that any planar map can be colored with only four colors. It was proved at U. Illinois in 1976 by Kenneth Appel and Wolfgang Haken. It required a computer program to check almost 2000 special cases. This computer-assisted proof was controversial at the time, but became accepted after the computerized search had been replicated a couple times.
Notice that graph coloring is NP complete. We don't know for sure if NP problems require polynomial or exponential time, but we suspect they require exponential time. However, many practical applications can exploit domain-specific heuristics (e.g. linear scan for register allocation) or loopholes (e.g. ok to have small conflicts in final exams) to produce fast approximate algorithms.
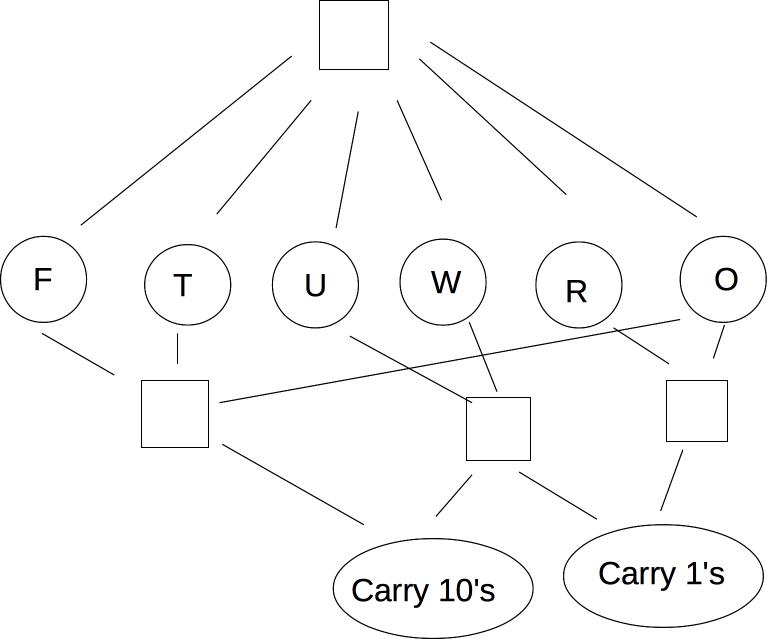
Cryptarithmetic is another classic CSP problem. Here's an example:
T W O
+ T W O
---------
= F O U R
We can make this into a CSP model as follows:
"Addition works as intended" can be made concrete with these equations, where C_1 and C_10 are the carry values.
O + O = R + 10 * C_1
W + W + C_1 = U + 10*C_10
T + T + C_10 = O + 10*F
"All different" and the equational constraints involve multiple variables. Usually best to keep them in that form, rather than converting to binary. We can visualize this using a slightly different type of graph with some extra nodes:
from
Wikipedia
Sudoku can be modelled as a CSP problem,
We can also use this framework to model scheduling problems, e.g. planning timing and sequence of operations in factory assembly.