Recall that Bayes net inference is polynomial time (i.e. reasonably efficient) Bayes nets that are "polytrees." A polytree is a graph that has no cycles if you consider the edges to be non-directional. But what if our Bayes net wasn't a polytree?

Junction tree algorithm

If your Bayes net is not a polytree, the junction tree algorithm will convert it to a polytree. This can allow efficient inference for a wider class of Bayes nets.

At a very high level, this algorithm first removes the directionality on the edges of the diagram. It then adds edges between nodes which aren't directly connected but are statistically connected (e.g. parents with a common child). This is called "moralization." It also adds additional edges to break up larger cycles (triangulaization). Fully-connected groups of nodes (cliques) are then merged into single nodes.

\(\rightarrow \) Moralize \(\rightarrow \)

\(\rightarrow \) Merge cliques into single nodes \(\rightarrow \)

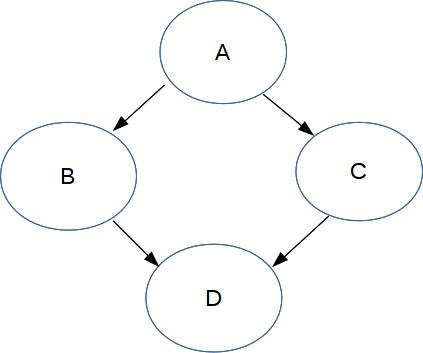
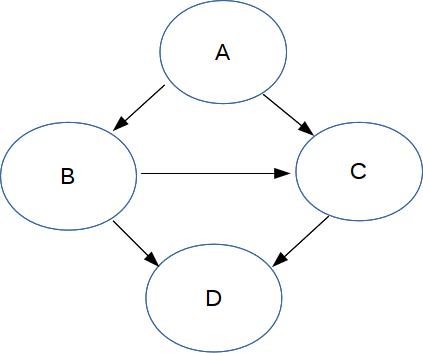
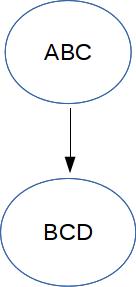
When the output diagrams are reasonably simple, they can then be used to generate solutions for the original diagram. (Long story, beyond the scope of this class.) However, this isn't guaranteed to work: the output graphs can be as complex as the original Bayes net. For example, notice that the new composite variable ABC has 8 possible values, because it's standing in for three boolean variables.

Quick review: NP complete

A decision problem is in NP (non-deterministic polynomial time) if you can provide a succinct (polynomial time verifiable) justification that a "yes" answer is correct. An example is whether a graph can be colored with k colors: just show us the coloring.

Problems in NP are widely believed to require exponential time. However, it is an open question whether there might be a better algorithm using only polynomial time.

A problem X is NP complete if a polynomial time algorithm for X would allow us to solve all problems in NP in polynomial time.

A very standard NP complete problem is 3SAT. The input 3SAT is a logical expression like this:

\(P = (X \text{ or } Y \text{ or } Z) \ \text{ and }\ (X \text{ or } \neg Y \text{ or } \neg Z) \ \text{ and }\ (X \text{ or } W \text{ or } Y) \)

Our algorithm must determine whether there is a set of input true/false values (for W, X, Y, Z) that will make the whole expression true. The input expression (P) must have the following form

• It's the AND of a series of terms.
• Each term is the OR of up to 3 variables (plain or negated).

Bayes net inference is NP complete

We can prove that Bayes net inference is NP complete, by showing how to use Bayes Net inference to construct an algorithm for 3SAT. Suppose we have a 3SAT logical expression:

\(P = (X \text{ or } Y \text{ or } Z) \ \text{ and }\ (X \text{ or } \neg Y \text{ or } \neg Z) \ \text{ and }\ (X \text{ or } W \text{ or } Y) \)

We convert it to a Bayes net that looks like this

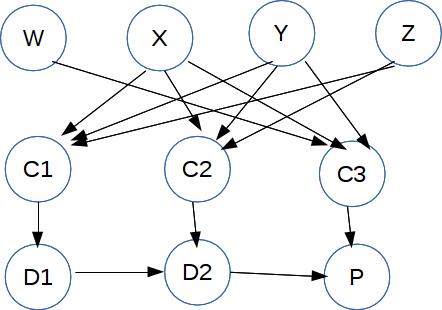
The top row of nodes are the input variables. The nodes C1, C2, C3 represent the terms. E.g. C1 represents \((X \text{ or } Y \text{ or } Z)\). Their associated probability tables simulate an OR of their inputs. The nodes D1, D2, and P assemble the full logical expression, using probability tables that simulate the AND of their inputs. So D2 represents

\((X \text{ or } Y \text{ or } Z) \ \text{ and }\ (X \text{ or } \neg Y \text{ or } \neg Z) \)

Our inference problem is whether we can find values for the input variables W,X,Y,Z that will give us a non-zero output probability value for P.

Bottom line

So, we have good and bad news about Bayes net inference:

• A useful range of examples can be solved efficiently. These include hidden Markov models (HMM's) which we'll see next week.
• Other examples probably require exponential time. Their values can be approximated using sampling methods beyond the scope of this course.

Further reading

A Brief Introduction to Graphical Models and Bayesian Networks by Kevin Murphy (1998)