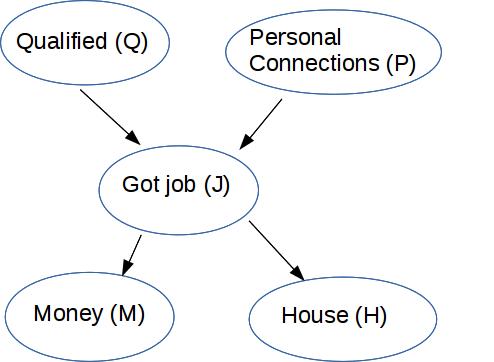
We'd like to use Bayes nets for computing most likely state of one node (the "query variable") from observed states of some other nodes. For example:
In addition to the query and observed nodes, we also have all the other nodes in the Bayes net. These unobserved/hidden nodes need to be part of the probability calculation, even though we don't know or care about their values.
We'd like to do a MAP estimate. That is, figure out which value of the query variable has the highest probability given the observed effects. Recall that we use Bayes rule but omit P(effect) because it's constant across values of the query variable. So we're trying to optimize
\(\begin{eqnarray*} P(\text{ cause } \mid \text{ effect }) &\propto& P(\text{ effect } \mid \text{ cause }) P(\text{ cause }) \\ &=& P(\text{ effect },\text{ cause }) \end{eqnarray*} \)
So, to decide if someone was qualified given that we have noticed that they have money and a house, we need to estimate \( P(q \mid m,h) \propto P(q,m,h)\). We'll evaluate P(q,m,h) for both q=True and q=False, and pick the value (True or False) that maximizes P(q,m,h).
To compute this, \(P(q,m,h)\), we need to consider all possibilities for how J and P might be set. So what we need to compute is
\(P(q,m,h) = \sum_{J=j, P=p} P(q,m,h,p,j) \)
P(q,m,h,p,j) contains five specific values for the variables Q,M,H,P,J. Two of them (m,h) are what we have observed. One (q) is the variable we're trying to predict. We'll do this computation twice, once for Q=true and once for Q=false. The last two values (j and p) are bound by the summation.
Notice that \(P(Q=true,m,h)\) and \(P(Q=false,m,h)\) do not necessarily sum to 1. These values are only proportional to \(P(Q=true|m,h)\) and \(P(Q=false|m,h)\), not equal to them.
If we start from the top of our Bayes net and work downwards using the probability values stored in the net, we get
\(\begin{align}P(q,m,h) &= \sum_{J=j, P=p} P(q,m,h,p,j) \\ &= \sum_{J=j, P=p} P(q) * P(p) * P(j \mid p,q) * P(m \mid j) * P(h \mid j) \end{align} \)
Notice that we're expanding out all possible values for three variables (q,j,p). This will become a problem for problems involving more variables, because k binary variables have \(2^k \) possible value assignments.
Let's look at how we can organize our work. First, we can simplify the equation, e.g. move variables outside summations like this
\( P(q,m,h) = P(q) * \sum_{P=p} P(p) * \sum_{J=j} P(j \mid p,q) * P(m \mid j) * P(h \mid j) \)
Second, if you think through that computation, we'll have to compute \(P(j \mid p,q) * P(m \mid j) * P(h \mid j) \) four times, i.e. once for each of the possible combinations of p and j values.
But some of the constituent probabilities are used by more than one branch. E.g. \( P(h \mid J=true) \) is required by the branch where P=true and separately by the branch where P=false. Se we can save significant work by caching such intermediate values so they don't have to be recomputed. This is called memoization or dynamic programming.
If work is organized carefully (a long story), inference takes polynomial time for Bayes nets that are "polytrees." A polytree is a graph that has no cycles if you consider the edges to be non-directional (i.e. you can follow the arrows backwards or forwards).