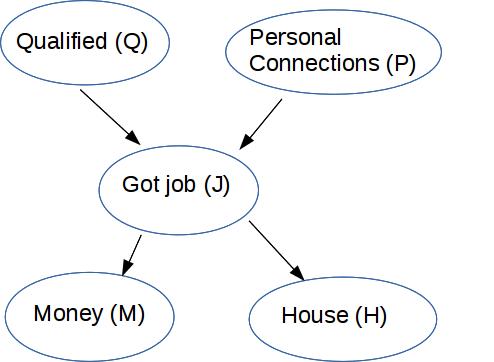
Let's remember how to understand the Bayes net diagram above. We have some number of boolean (true/false) variables, five in this case. The edges in the diagram show which probabilities depend on one anohter. For each node, we store the probability of that variable in terms of the probabilities of its parents. For example
Recall from discrete math: a partial order orders certain pairs of objects but not others. It has to be consistent, i.e. no loops. So we can use it to draw a picture of the ordering with ancestors always higher on the page than descendents.
The arrows in a Bayes net are like a skeleton of a partial order: just relating parents to their children. The more general ancestor relationship is a true partial order.
For any set with a partial order, we can create a "topological sort." This is a total/linear order of all the objects which respects the partial order. That is, a node always follows its ancestors. Usually there is more than one possible topological sort and we don't care which one is chosen.
A Bayes net is a directed acyclic (no cycles) graph (called a DAG for short). So nodes are partially ordered by the ancestor/descendent relationships.
Each node is conditionally independent of its ancestors, given its parents. That is, the ancestors can ONLY influence node A by working via parents(A)
Suppose we linearize the nodes in a way that's consistent with the arrows (aka a topological sort). Then we have an ordered list of nodes \( X_1, ..., X_n\). Our conditional independence condition is then
For each k, \(P(X_k | X_1,...,X_{k-1}) = P(X_k | \text{parents}(X_k))\)
We can build the probability for any specific set of values by working through the graph from top to bottom. Suppose (as above) that we have the nodes ordered \(X_1,...,X_n\). Then
\( P(X_1,...,X_n) = \prod_{k = 1}^n P(X_k | \text{parents}(X_k)) \)
\( P(X_1,...,X_n) \) is the joint distribution for all values of the variables.
In \( \prod_{k = 1}^n P(X_k | \text{parents}(X_k)) \), each term \( P(X_k | \text{parents}(X_k)) \) is the information stored with one node of the Bayes net.
In this computation, we're starting from the causes (also called "query variables") such as bad food and virus above. Values propagate through the intermediate ("unobserved") nodes, and eventually we produce values for the visible effects (go to McKinley, email instructors). Much the time, however, we would like to work backwards from the visible effects to find the most likely cause(s).
Suppose we have n variables. Suppose the maximum number of parents of any node in our Bayes net is m. Typically m will be much smaller than n.
Suppose we know the full full joint probability distribution for our variables and want to convert this to a Bayes net.. We can construct a Bayes net as follows:
Put the variables in any order \(X_1,\ldots,X_n\).
For k from 1 to nChoose parents(\(X_k\)) to contain all variables from \(X_1,\ldots,X_{k-1}\) that \(P(X_k)\) depends on.
The output Bayes net depends on the order in which we process the variables. If our variable order is Q, P, J, M, H, then we get the above Bayes net, which contains 10 probability values. (1 each for Q and P, 2 each for M and H, 4 for J).
Suppose we use the variable order M, H, J, Q, P. Then we proceed as follows:
M: no parents
H: isn't independent of M (they were only conditionally independent given J), so M is its parent
J: P(J) isn't independent of P(M) or P(H), nor is P(J | M,H) = P(J | H) so both of these nodes have to be its parents
Q: P(Q | J,M,H) = P(Q | J) so just list J as parent
P: probility depends on both J and Q
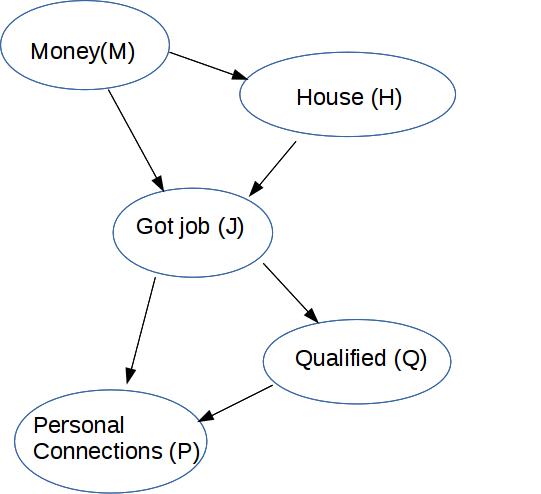
This requires that we store 13 probability numbers: 1 for M, 2 for H, 4 for J, 2 for Q, 4 for P.
So the choice of variable order affects whether we get a better or worse Bayes net representation. We could imagine a learning algorithm that tries to find the best Bayes net, e.g. try different variable orders and see which is most compact. In practice, we usually depend on domain experts to supply the causal structure.