General guidelines

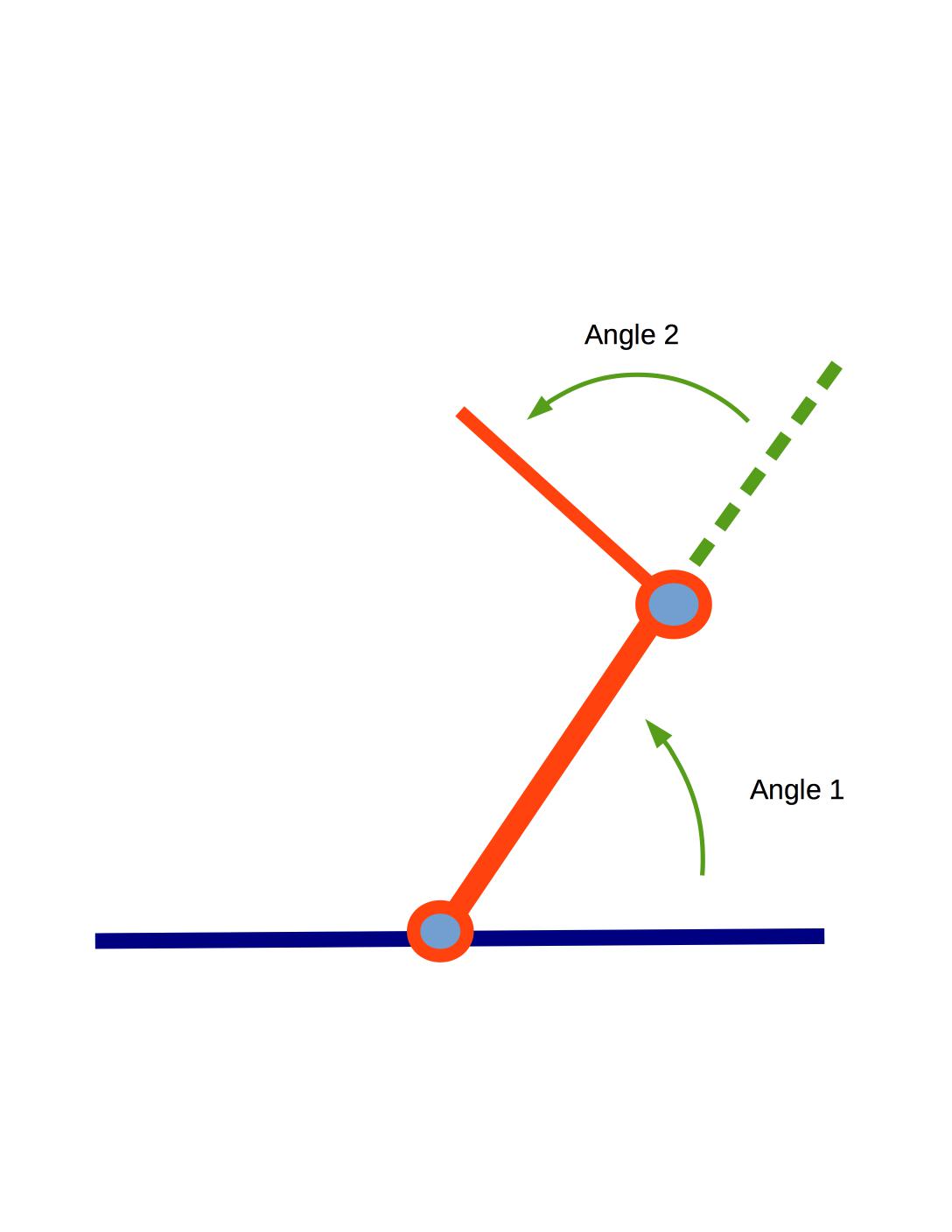
You are given a two-link arm in 2D space as explained in class. This arm has two links of length $L_1$ and $L_2$ respectively. The arm is free to rotate about its base that is pivoted on the ground and link-2 can rotate about the joint where it connects with link-1. Let's use $\alpha$ for the angle between the link-1 and the ground (equivalent to $\theta_1$). Let's use $\beta$ for the angle between link-2 and link-1 (equivalent to $\theta_2$). 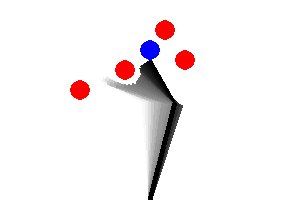The robot is shown at the top of the page with visualization of $\theta_1$ and $\theta_2$. Note that the angles are measured counter-clockwise.

For each planning problem, you will be given:

• The starting angles for the robotic arm.
• The locations (x,y) and radius r of circular goals.
• The locations (x,y) and radius r of various circular obstacles.

    [BasicMap]
    Window : (300, 200)                     # (width, height)
    ArmBase : (150, 200)                    # (x-coordinate, y-coordinate)
    ArmLinks : [
                    (100, 95, 5, (0, 180)), # (length, initial angle, padding distance, (min angle, max angle)
                    (50, 60, 5, (-150, 150)),
               ]
    Obstacles : [
                    (125, 70, 10),          # (x-coordinate, y-coordinate, radius)
                    (80, 90, 10),
                    (165, 30, 10),
                    (185, 60, 10)
                ]
    Goals : [
                (150, 50, 10),               # (x-coordinate, y-coordinate, radius)
                (100, 50, 10)
            ]

Part 1: Geometry

The first problem in geometry is to compute (start, end) position of each arm link for the given $\alpha$ and $\beta$. The base position, initial angle, and length of link-1 is given in theconfiguration, so the end position of link-1 can be computable. The end position becomes the base position of link-2. Then, the end position of link-2 can be also computable for the given length and $\beta$. We kindly provide two helper classes: Arm and ArmLink. One arm can have at least 1 arm link and at most 3 arm links. You do not have to modify these two classes. To solve MP2, the following Arm methods would be useful:

arm.py

• getBase(): Return (x, y) of the arm base
• getArmAngle(): Return relative angles of all arm links. If there are two arm links, the return value would be (alpha, beta)
• getArmLimit(): Return (min angle, max angle) of all arm links
• setArmAngle(angles): Set angles(alpha, beta) for all arm links
• getEnd(): Returns (x, y) of the arm tip
• getArmPos(): Returns (start, end) of all arm links
• getArmPosDist(): Returns (start, end, distance) of all arm links

The relationship among arm links are already defined in Arm. What you need to define is how to compute the end position of the arm link for the given length and angle. To this end, you may need to implement the following function:

geometry.py

• computeCoordinate(start, length, angle): Return the end position for the given start position and length. Please round down the trigonometry function to integer.

Once you correctly define the above function, getEnd() and getArmPos() functions as defined above would perform as expected.

The next geometry problem is then to check whether

• the arm tip (the open end of the arm) touches or is inside the goal.
• the arm runs into obstacles, i.e. the distance is the less than the obstacle's padding distance. Note that the goal should be also considered as an obstacle with 0 padding distance unless the robotic arm tip touches it.
• all parts of the arm remain in the given window.

To do this, you need to implement the following functions:

geometry.py

• doesArmTipTouchGoals(armEnd, goals): Return True if the given arm tip position is anywhere in the given goals, including the boundary. Otherwise return False.
• doesArmTouchObjects(armPosDist, obstacles, isGoal): Return True if the given arm touches any obstacle, including the boundary. Otherwise return False.
• isArmWithinWindow(armPos, window): Return True if all parts of the arm are within the window. Otherwise return False.

The second part of this MP is to transform the generated 2D map to the maze in MP1. The rows and columns in the maze match to alpha and beta, i.e. the joint angles of the robotic arm. The number of rows and columns of the maze can be decided by 1) degree granularity (angular resolution) and 2) minimum / maximum value of the angle. The number of positions in the row or column is $\frac{\text{maxangle} -\text{minangle}}{\text{granularity}} + 1$. For example, if range of alpha is (45, 135) and degree granularity is 2, then the number of rows becomes $46 = \frac{135-45}{2}+1$. When the output of the division is not an integer, round it down.

Once the maze size is determined, then you need to fill the starting point, walls, goals in the maze.

• Initial alpha and beta would be the starting point.
• The alpha and beta at which the arm tip touches the goals would be the goals in the maze.
• The alpha and beta at which the arm cannot reach (touching the obstacles, touching the goal but not using the arm tip, reaching outside of the window, etc) would be the walls in the maze.
• To contruct walls and goals, you need to use geometry functions defined in Part 1.

The naive approach is to do bruteforce checking for all pairs of alpha and beta. Or you can apply some smart short-cut techniques to bypass unnecessary checking. For example, if the first link already hits an obstacle, you may not need to check beta for that alpha. Although you use your own shortcut algorithm, the output maze should look same as the result of the bruteforce algorithm.

Your main effort for Part 2 would be to implement the following function.

transform.py

• transformToMaze(arm, goals, obstacles, window, granularity): This function will return the maze instance created based on the given input arguments.
• The input arguments are:
  • arm (Arm): arm instance
  • goals (list): [(x, y, r)] of goals, where x and y are coordinates, and r is radius
  • obstacles (list): [(x, y, r)] of obstacles, where x and y are coordinates, and r is radius
  • window (tuple): (width, height) of the window
  • granularity (int): unit of increasing/decreasing degree for angles
• Hint: use utils.py.

The following images are examples of output maze for Test1 above. The left image has the finer granularity and the right image has the coarser granularity. As you can see, the maze resolution is determined depending on the input granularity. As can be seen, you should be able to handle any level of granularity. Granularity is a natural number for simplicity.

mp2.py does not generate the image of maze map as above. If you would like to visualize the map, you should run mp2.py to export the maze to a text file, which is an input file of mp1.py. Then, you can run your mp1.py to create the maze map. That is,

python3 mp2.py --map Test1 --config test_config.txt --save-maze [MAZEFILE_PATH]
python3 mp1.py [MAZEFILE_PATH]

Now we are back to MP1. You can exploit your previous search functions to find the path to exit the maze with minor modifications. In MP2, You will use bfs to find a optimal path. You do not have to worry about multiple goals (dots). Your search function should be terminated after your agent reaches any of goals, Otherwise, it would take ages for agents to visit all the goals in the maze. If no path is found, the search function should return None instead of an empty list. The final state of the robotic arm for Test1 is shown in the left image. You can leave the footprint of the arm rotation in every n move with "--trajectory n" option. The corresponding explored shortest path for the maze is shown in the right image.

Generalize your computation to robots with one and three links. Although there are multiple ways to implement this, we require that your configuration space map will need to be 3-dimensional to pass the autograder. That is, given 1-link, 2-link, or 3-link robot arm, your map configuration should always maintain 3 dimensions, and the path you return should be a list of 3-element tuples. For example, given 1-link robot arm, your map would have size (alpha, 1, 1).

You will need to modify "maze.py" in this part as well as "search.py", "transform.py" and "geometry.py". You are free to change the function signature in maze.py, except those specified in the following:

• get_map() in maze.py. The map returned should have 3 dimensions in the order of (alpha, beta, gamma)
• get_start() in maze.py. The start position returned should have 3 dimensions in order of (alpha, beta, gamma)
• search() in search.py
• transformToMaze() in transform.py

Provided Code Skeleton