For each variable X, maintain set D(X) containing all possible values for X.
Run DFS. At each search step:
We may have multi-variate constraints, e.g. sudoku row/column/block values all different. However, let's consider only two-variable constraints for now.
Which variable should we pick?
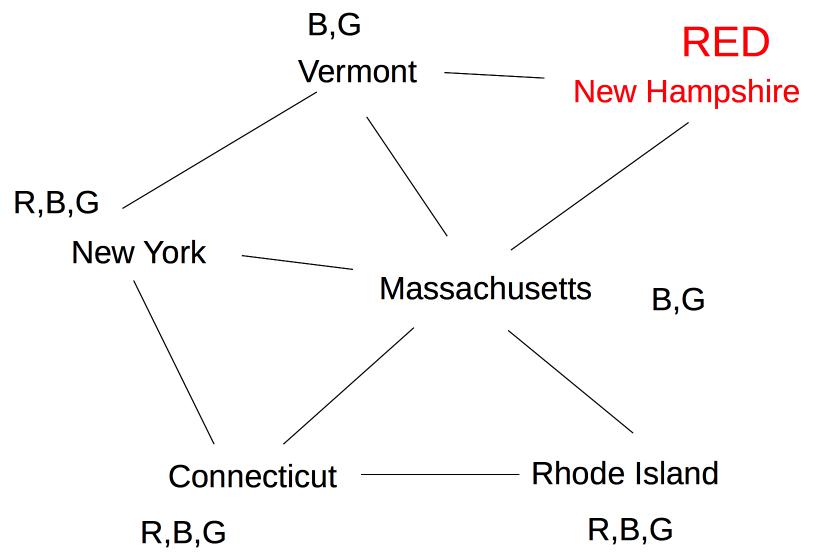
Suppose we are coloring the following graph with 3 colors (red, green, blue).
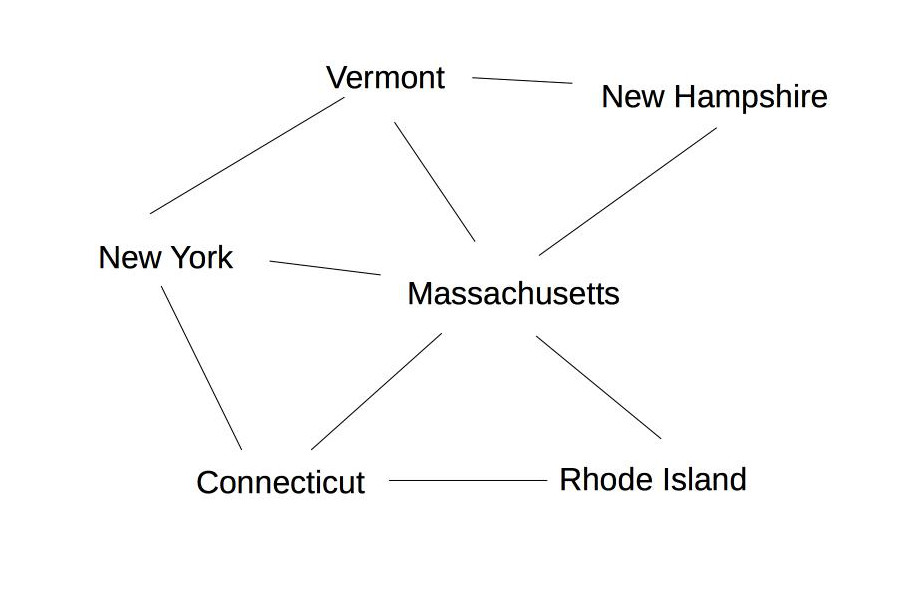
All states have three possible color values, so we use heuristic (b) and pick a color for Massachusetts:
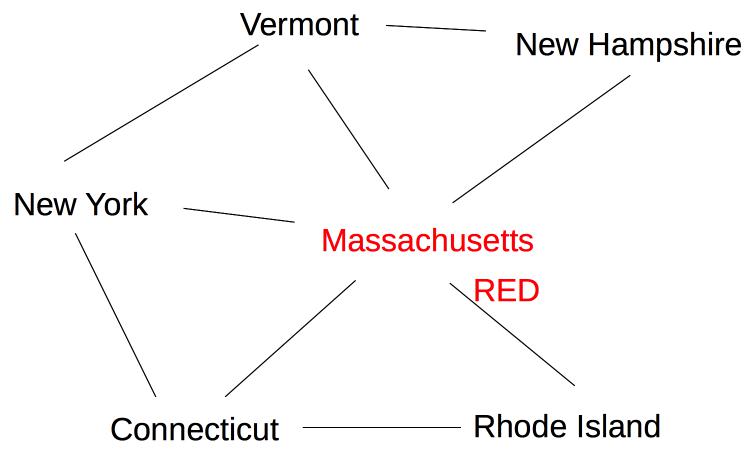
The five remaining states are still tied on (a), so we use heuristic (b) to pick one of the states with three neighbors (Vermont):
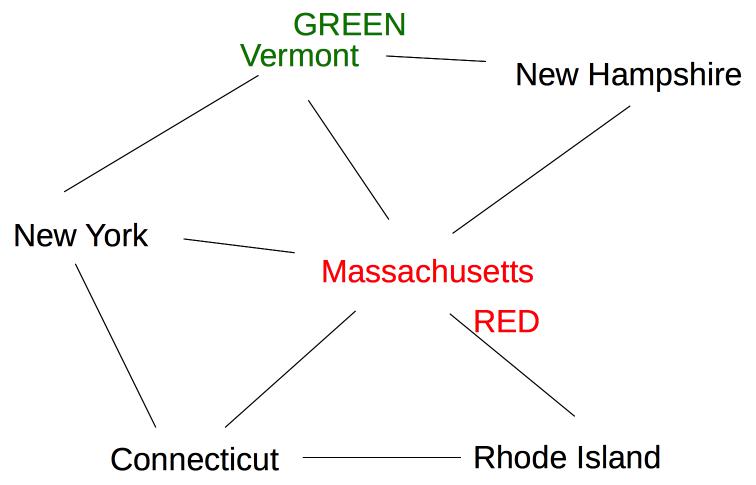
Now two states (New York and New Hampshire) have only one possible color value (blue), so we color one of them next:
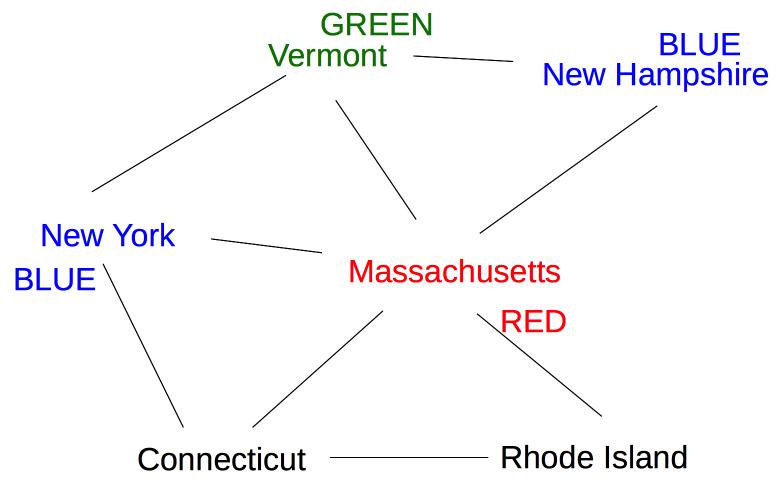
Once we've chosen a variable, what is a good value to choose?
For example, suppose we're trying to pick a value for the lower left node in the graph below. We should try Green first, because it leaves two color options open for the lower right node.
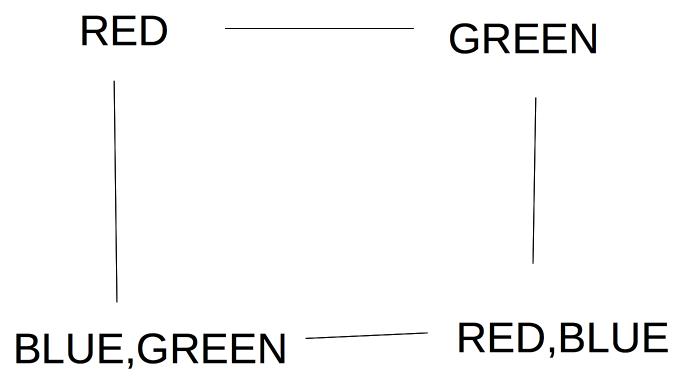
If this preferred choice doesn't work out, then we'll back up and try the other choice (Blue).
Solvers should be aware of any internal symmetries in the problem. For example, the map coloring problem doesn't care which color is which. So it doesn't matter which value we pick for the first variable (sometimes also some later choices). Similarly, there aren't really four distinct choices for the first column of n-queens, because reflecting the board vertically (or horizontally) doesn't change the essential form of the solution.
When we assign a value to variable X, forward checking only checks variables that share a constraint with X, i.e. are adjacent in the constraint graph. This is helpful, but we can do more to exploit the constraints. Constraint propagation works its way outwards from X's neighbors to their neighbors, continuing until it runs out of nodes that need to be updated.
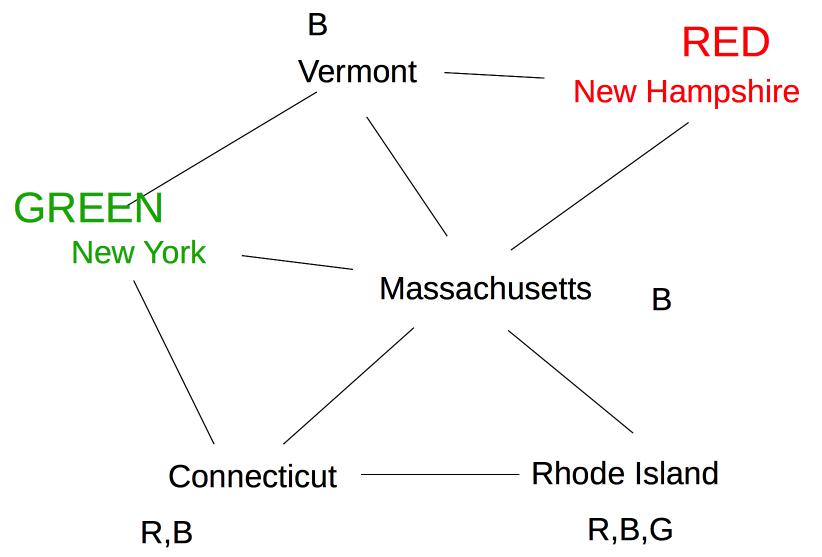
Suppose we are coloring the same state graph with {Red,Green,Blue} and we decide to first color New Hampshire red:
Forward checking then removes Red from Vermont and Massachusetts. Suppose we now color New York Green. Forward checking removes Green from its immediate neighbors, giving us this:
At this point, forward checking stops. Constraint propagation continues. Since Massachusetts now has fewer possible values, its neighbor Connecticut also needs to be updated.
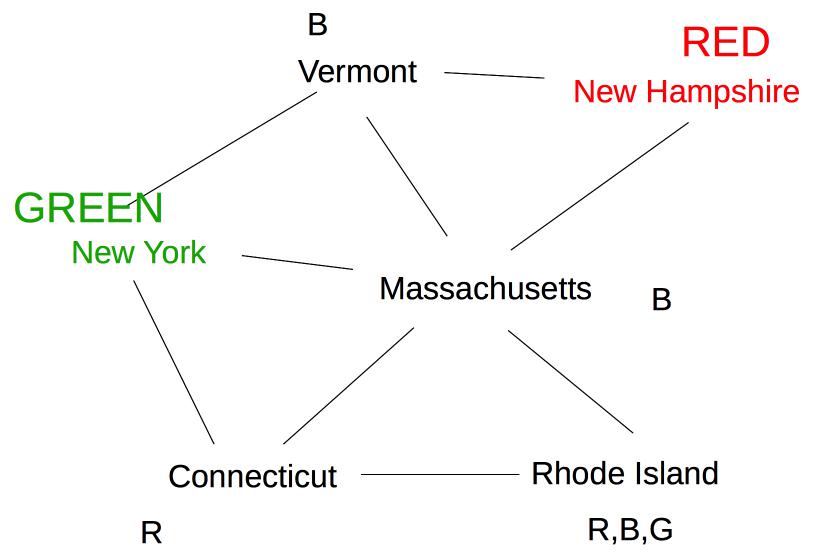
Rhode Island is adjacent to Massachusetts and Connecticut, so its options need to be updated:
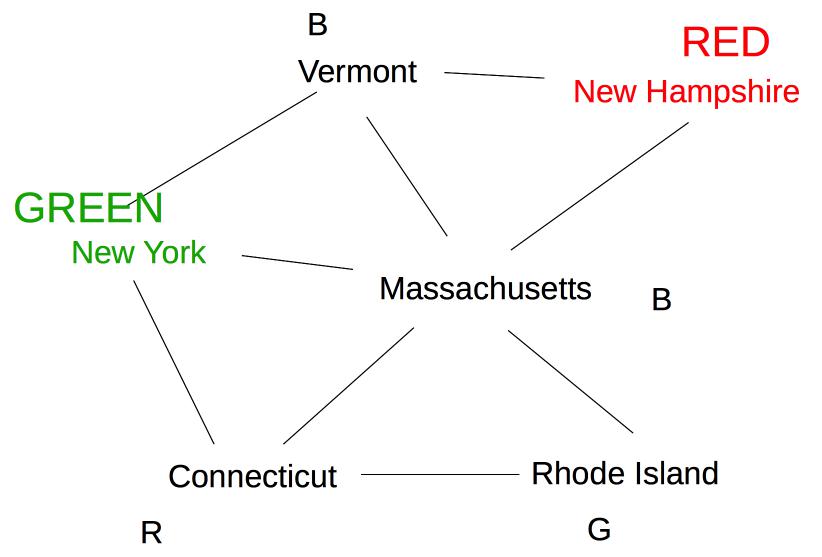
Finally, Vermont is a neighbor of Massachusetts, so update its options.
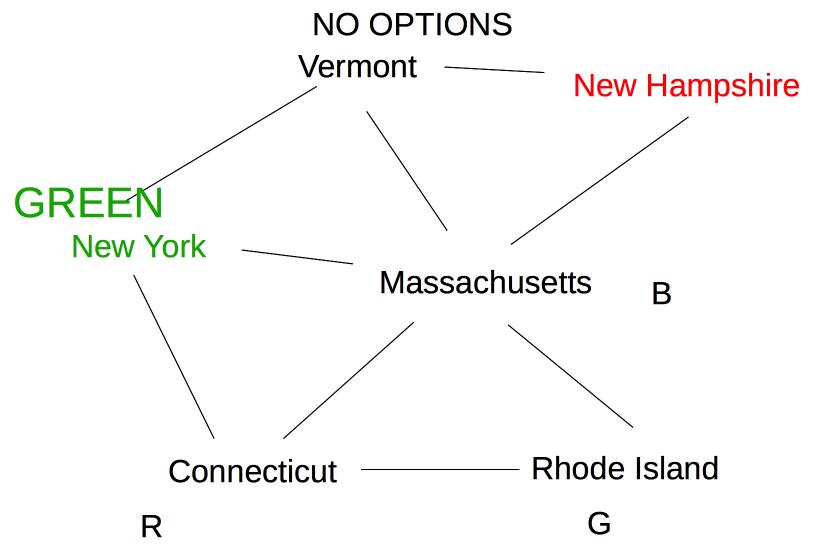
Since this leaves Vermont with no possible values, we backtrack to our last decision point (coloring New York Green).
The exact sequence of updates depends on the order in which we happen to have stored our nodes. However, constraint propagation typically makes major reductions in the number of options to be explored, and allows us to figure out early that we need to backtrack.
Constraint propagation greatly reduces the number of assignments we need to search. Also it detects failure (triggers backtracking) much earlier. It can be used at two points in the search
Sometimes constraint propagation can completely solve a problem by itself. Line labelling from Lana Lazebnik based on David Waltz's 1972 thesis. Contemporary video of the solver in action.
Fullly working contraint propagation algorithm AC-3, by David Waltz and Alan Mackworth (1977).
The constraint relationship between two variables ("some constraint relates the values of X and Y") is symmetric. For this algorithm, however, we view constraints between variables ("arcs") as ORDERED pairs. So the pair (X,Y) will represent contraint flowing from Y to X.
Revise(X,Y) prunes values of D(X) that are inconsistent with what's currently in D(Y).
Maintain queue of pairs ("arcs") that still need attention.
Initialize queue. Two options
Loop:
Stop when queue is empty
Near the end of AC-3, we push all arcs (C,X) onto the queue, but we don't push (Y,X). Why don't we need to push (Y,X)?
Another approach to CSP problems involves randomly picking a full set of variable assignments, then trying to tweak it into a legal solution. At each step, we change the value of one variable to try to reduce the number of conflicts.
Hill-climbing n-queens (from Lana Lazebnik, Fall 2017).
This seems to be how people solve certain complicated graph-coloring problems such as avoiding/reducing conflicts in final exam scheduling.
Hill climbing can be very effective, but it can get stuck in local optima. So algorithms often add some randomization:
Maybe speech recognition caused unwanted dollhouse orders or maybe it never happened.