Now consider a polygonal robot moving around in 2D. For example, a car or truck moving around the roads near the Siebel Center
(from Google maps)
To specify the robot's position, we need to give its (x,y) position and also its orientation. (In-class demo of a polygonal car moving around some streets.) So the robot's configuration space is three dimensional. See the following slides for two worked examples from Howie Choset:
So this 2D problem with simple polygonal obstacles has a 3D configuration space with quite complex obstacles.
Configuration spaces can get very large, esp. when they are high dimensional (e.g. 3D situations, multi-joint robot arms). They also present the planner with an excessively large set of choices, e.g. all the possible paths through a big open area. Some ways to keep representations simple:
Obviously, the robot's path should reach the goal and be reasonably short. However, in most practical situations, it should also
It's risky to get too close to obstacles. We could easily hit the obstacle if there are any errors in our model of our shape, our position, and/or the obstacle position. Sharp changes in orientation or speed may be impossible for the robot to execute and/or cause excessive wear on the joints.
We can divide a configuration space into two sets: free space and obstacles. Roadmap methods convert free space into a graph structure, made up of
This creates a compact representation of free space, partly by giving the robot only one route through each open area.
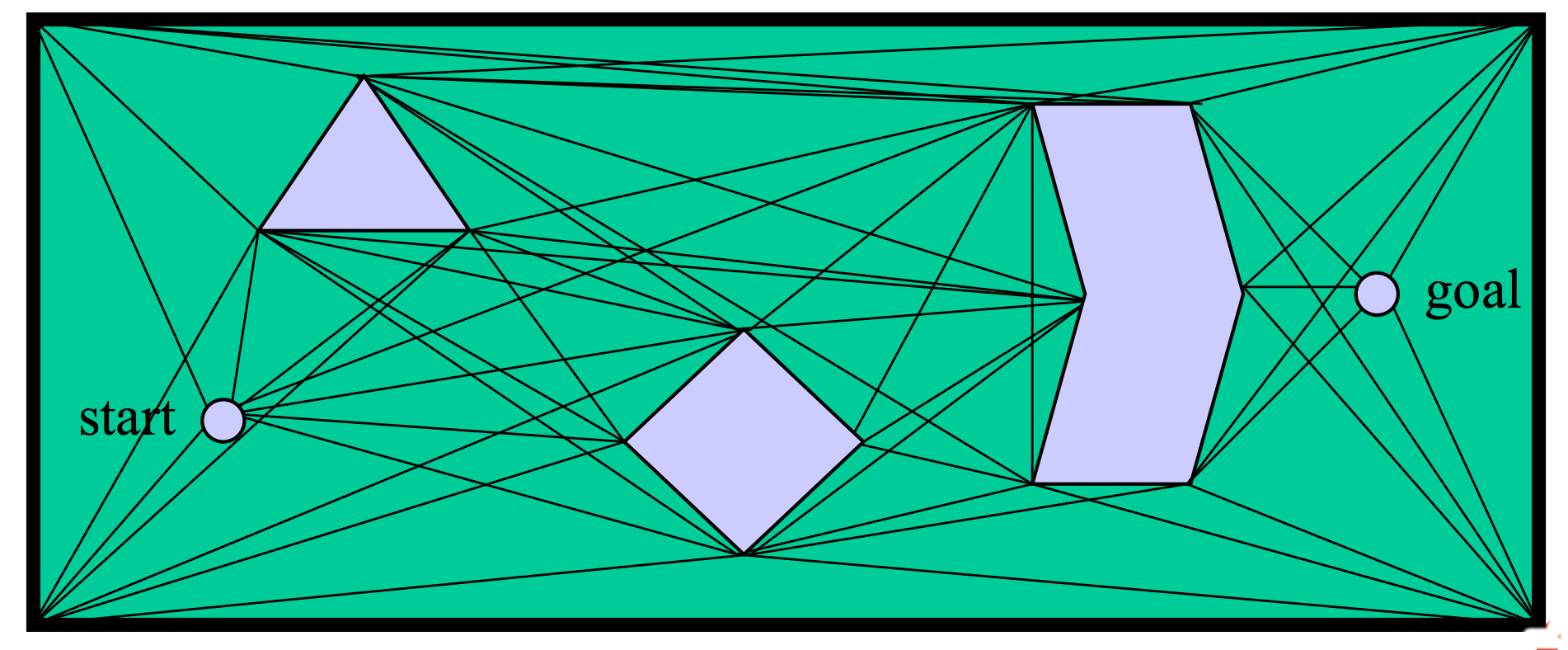
A visibility graph uses vertices of objects as way points. Edges are straight lines connecting vertices. This roadmap can be constructed incrementally, directly from a polygonal representation of the obstacles: Visibility Graph Construction
(from Howie Choset)
Edges in visibility graphs tend to touch vertices of obstacles and skim along obstacle edges. Unless you artificially enlarge the robot and/or obstacles, these paths won't be very safe.
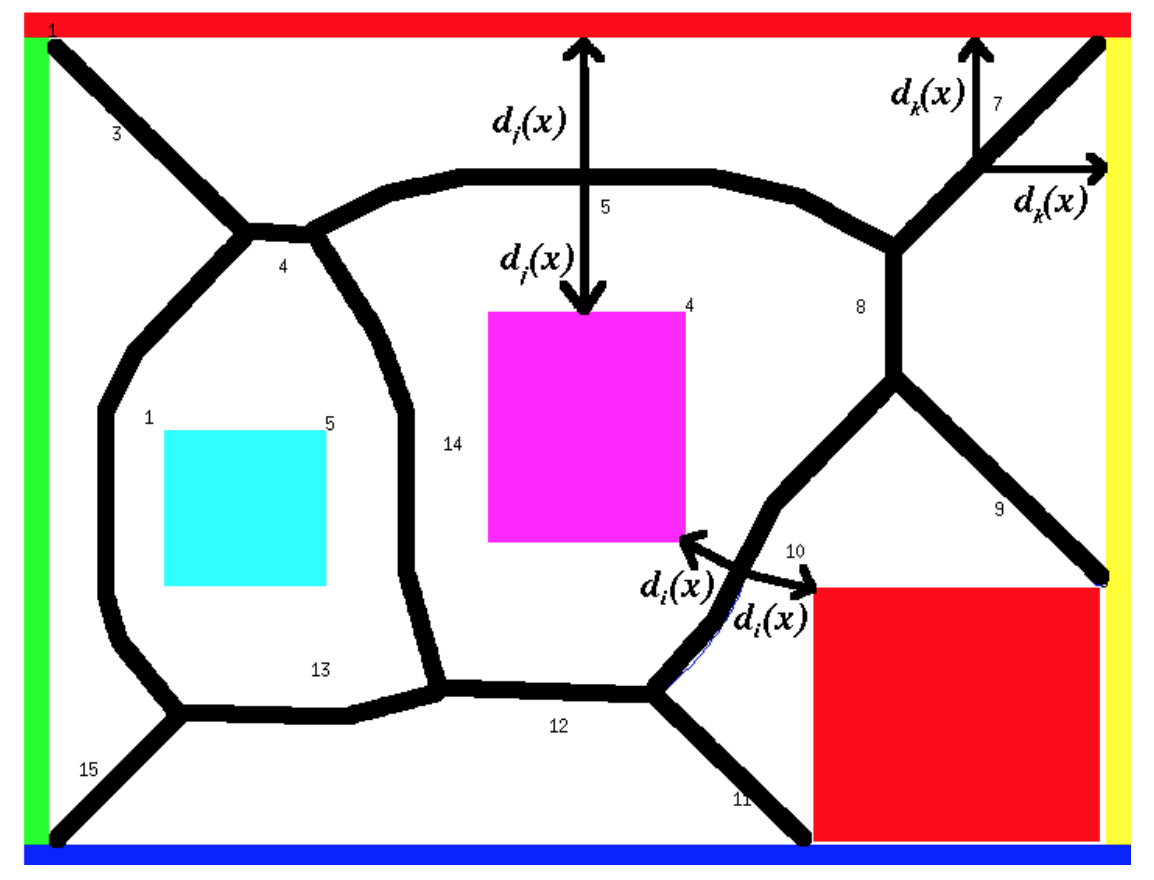
Another class of methods convert freespace into a skeleton that goes through the middle of regions. Paths are then constructed in three parts:
(from Howie Choset)
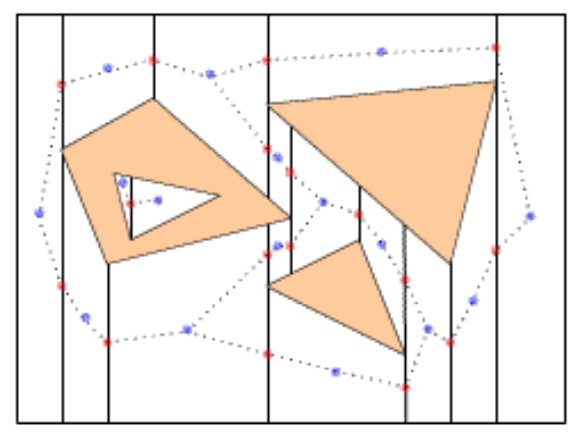
The cell decomposition below divides free space somewhat more arbitrarily into trapezoids aligned with the coordinate axes. Way points are then located in the middle of each trapezoid and the middles of its edges.
(from Philippe Cheng, MIT, 2001)
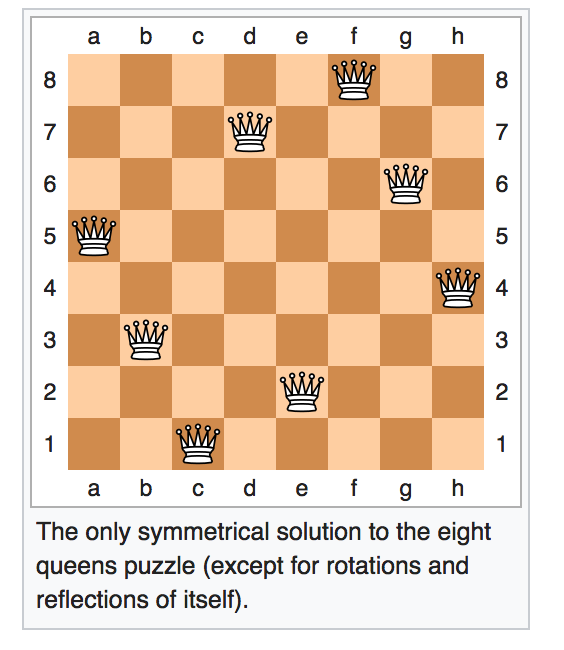
Remember that a queen in chess threatens another piece if there is a direct path between the two either horizontally, or vertically, or diagonally. In the "n queens problem," we have to place n queens on a n by n board so that no queen threatens another. Here is a solution for n=8:
From Wikipedia
In basic search problems, we know the goal and want to find a path to it. In a constraint-satisfaction problem, we have only a test for whether a state is a goal. Our problem is to find a goal state. The path to the goal is only temporary scaffolding.
The armies of ghost workers who help train AI algorithms.
An algorithm annotating news reports confused the Notre Dame fire with 9/11.