Since this class depends on data structures, which has discrete math as a prerequisite, most people have probably seen some version of BFS, DFS, and state graphs before. If this isn't true for you, this lecture probably went too fast. Aside from the textbook, you may wish to browse web pages for CS 173, CS 225, and/or web tutorials on BFS/DFS.

State graph representations

Key parts of a state graph:

• states (graph nodes)
• actions (graph edges, with costs)
• start state
• goal states (explicit list, or a goal condition to test)

Task: find a low-cost path from start state to a goal state.

Some applications want a minimum-cost path. Others may be ok with a path whose cost isn't stupidly bad (e.g. no loops).

Road maps

We can take a real-world map (below left) and turn it into a graph (below right). Notice that the graph is not even close to being a tree. So search algorithms have to actively prevent looping, e.g. by remember which locations they've already visited.

Mapping this onto a state graph:

• states are towns
• actions are going down a road
• edge costs are distances

On the graph, it's easy to see that there are many paths from Northampton to Amherst, e.g. 8 miles via Hadley, 31 miles via Williamsburg and Whately.

Mazes

Left below is an ASCII maze of the sort used in 1980's computer games. R is the robot, G is the goal, F is a food pellet to collect on the way to the goal. We no longer play games of this style, but you can still find search problems with this kind of simple structure. On the right is one path to the goal. Notice that it has to double back on itself in two places.

Modelling this as a state graph:

• states are (x,y) positions
• actions are moves left, right, up, down
• edge costs are constant

Some mazes impose tight constraints on where the robot can go, e.g. the bottom corridor in the above maze is only one cell wide. Mazes with large open areas can have vast numbers of possible solutions. For example, the maze below has many paths from start to goal. In this case, the robot needs to move 10 steps right and 10 steps down. Since there are no walls constraining the order of right vs. downward moves, there are \(20 \choose 10 \) paths of shortest length (20 steps), which is about 185,000 paths. We need to quickly choose one of these paths rather than wasting time exploring all of them individually.

Game mazes also illustrate another feature that appears in some AI problems: the AI gains access to the state graph as it explores. E.g. at the start of the game, the map may actually look like this:

Puzzle

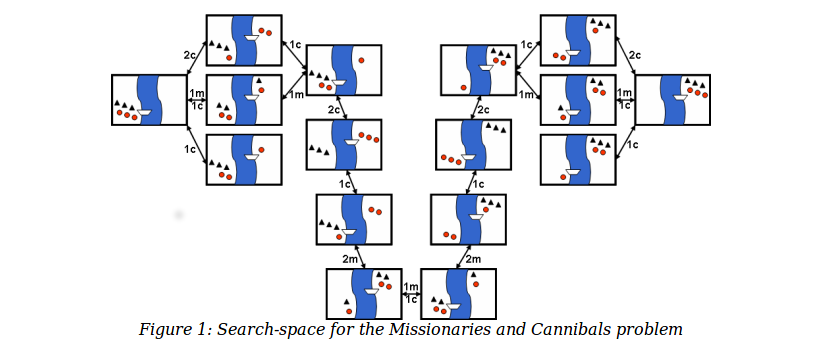
States may also be descriptins of the real world in terms of feature values. For example, consider the Missionaries and Cannibals puzzle. In the starting state, there are three missionaries, three cannibals, and a boat on the left side of a river. We need to move all six people to the right side, subject to the following constraints:

• The boat cannot carry more than two people at a time.
• The boat cannot move without at least one person on it.
• If there are both missionaries and cannibals on one side of the river, the cannibals cannot outnumber the missionaries. (Otherwise they will eat the missionaries.)

The state of the world can be described by three variables: how many missionaries on the left bank, how many cannibals on the left bank, and which bank the boat is on. The state space is shown below:

(from Gerhard Wickler, U. Edinburgh)

In this example

• states are sets of variable values
• actions are legal changes to these values
• edge costs often constant

Speech recognition

In speech recognition, we need to transcribe an acoustic waveform into to produce written text. We'll see details of this process later in the course. For now, just notice that this proceeds word-by-word. So we have a set of candidate transcriptions for the first part of the waveform and wish to extend those by one more word. For example, one candidate transcription might start with "The book was very" and the acoustic matcher says that the next word sounds like "short" or "sort."

In this example

• states are partial transcriptions of the input
• actions extend the transcription (e.g. by one word)
• edge costs reflect how well the new word matches the acoustic signal and whether the new word seems appropriate given the previous context.

Speech recognition systems have vast state spaces. A recognition dictionary may know about 100,000 different words. Because acoustic matching is still somewhat error-prone, there may be many words that seem to match the next section of the input. So the currently-relevant states are constructed on demand, as we search. Chess is another example of an AI problem with a vast state space.

Some high-level points

For all but the simplest AI problems, it's easy for a search algorithm to get lost.

• The graph has cycles.
• The state space is very large.
• There are many paths of similar quality.

The first of these can send the program into an infinite loop. The second and third can cause it to get lost, exploring states very far from a reasonable path from the start to the goal.

Our first few search algorithms will be uninformed. That is, they rely only on computed distances from the starting state. Next week, we'll see \(A^*\)). It's an informed search algorithm because it also uses an estimate of the distance remaining to reach the goal.

Basic search outline

A state is exactly one of

• not yet seen (can be a very large set in some applications)
• frontier, i.e. seen but we haven't explored its outgoing edges
• completely done (all outgoing edges followed)

Basic outline for search code

Loop until we find a solution

• take state off frontier
• follow outgoing edges to find neighbors
• add neighbors to frontier if not already seen

Data structure for frontier determines type of search

• BFS: queue
• DFS: stack (or implicit stack via recursion)
• UCS (uniform cost search) and \(A^*\): priority queue

BFS example

Let's find a route from Easthampton to Whately Using BFS. The actual best route is via Northampton, Florence, Hatfield (19 miles)

The frontier is stored as a queue. So we explore locations in rings, gradually moving outwards from the starting location. Let's assume we always explore edges left to right.

Start

Easthampton

Add neighbors of Easthampton

Westhampton, Northampton, South Hadley

Add neighbors of Westhampton

Northampton, South Hadley, Chesterfield, Williamsburg

Add neighbors of Northampton

South Hadley, Chesterfield, Williamsburg, Florence, Hadley

Add neighbors of South Hadley

Chesterfield, Williamsburg, Florence, Hadley, Amherst

Add neighbors of Chesterfield

Williamsburg, Florence, Hadley, Amherst, Goshen

Add neighbors of Williamsburg

... FOUND WHATELY

We return the path Westhampton, Williamsburg, Whately (length 28)

BFS properties:

• Solution is always optimal if and only if all edges have same cost.
• Frontier can get very large, often grows linearly with distance outwars from start.
• Must store all seen states to avoid looping.

Here is a fun animation of BFS set to music.

DFS example

The frontier is stored as a stack (explicitly or implicitly via recursive function calls). Again, we'll explore edges left to right. The frontier looks like:

Start

Easthampton

Add neighbors of Easthampton

Westhampton, Northampton, South Hadley

Add neighbors of Westhampton

Chesterfield, Williamsburg, Northampton, South Hadley

Add neighbors of Chesterfield

Goshen, Williamsburg, Northampton, South Hadley

Add neighbors of Goshen

... FOUND WHATELY

We return the path: Westhampton, Chesterfield, Goshen, Whateley (length 38)

DFS properties:

• Solution can be very far from optimal.
• Frontier stays small.
• May not terminate if state space is infinite.

Animation of DFS set to music. Compare this to the one for BFS.

Storing seen states

When searching a large state space, there can be a huge number of seen states. If states have to be instantiated for other reasons (e.g. a full map is loaded into memory), this is not a problem because we can simply add a mark bit to each state.

If states are generated dynamically, DFS can save a lot of memory as follows:

• Don't explicitly store seen states.
• Just check that we're not returning to a state that's on the stack or on the paths leading up to these states

The cost is that this version of DFS does redundant work because it has a poor memory for what it has already examined. This tradeoff can be good or bad depending on the structure of the state space.

Iterative deepening

We can dramatically improve the low-memory version of DFS by running it with a progressively increasing bound on the maximum path length. That is

For k = 1 to infinity

Run DFS but stop whenever a path contains at least k states.
Halt when we find a goal state

This is called "iterative deepening." Its properties

• Overall search behavior looks like BFS.
• Each iteration starts from scratch, forgetting all previous work.
• Uses very little memory.

Each iteration repeats the work of the previous one. However, the number of states increases very fast with depth. So running time is dominated by work in the last iteration.