Recap

Pieces of an MDP

• states s in S
• actions a in A
• transition probabilities P(s' | s,a)
• reward function R(s)
• policy $\pi(s)$ returns action

When we're in state s, we command an action $\pi(s)$. However, our buggy controller may put us into a variety of choices for the next state s', with probabilities given by the transition function P.

Bellman equation for best policy

$U(s) = R(s) + \gamma \max_{a \in A} \sum_{s' \in S} P(s' | s,a)U(s')$

Warning: Notational variant

Some authors use variants of the Bellman equation like this:

$V(s) = \max_a \sum_s' P(s' | s,a) [R(s,a,s') + \gamma V(s')]$

There is no deep change involved here. This is partly just pushing around the algebra. Also, passing more arguments to the reward function R allows a more complicated theory of rewards, i.e. depending not only on the new state but also the previous state and the action you used. If we use our simpler model of rewards, then this V(s) these can be related to our U(s) as follows

U(s) = R(s) + V(s)

Recap: Value iteration

Recall how we solve the Bellman equation using value iteration. let $U_t$ be the utility values at iteration step t.

• Initialize U(s) = 0 for all s
• For i=0 until values converge
  • $U_{i+1}(s) = R(s) + \gamma \max_{a \in A} \sum_{s' \in S} P(s' | s,a) U_i(s')$

This can take the gridworld problem (top left below) and produce the utility values (bottom left).

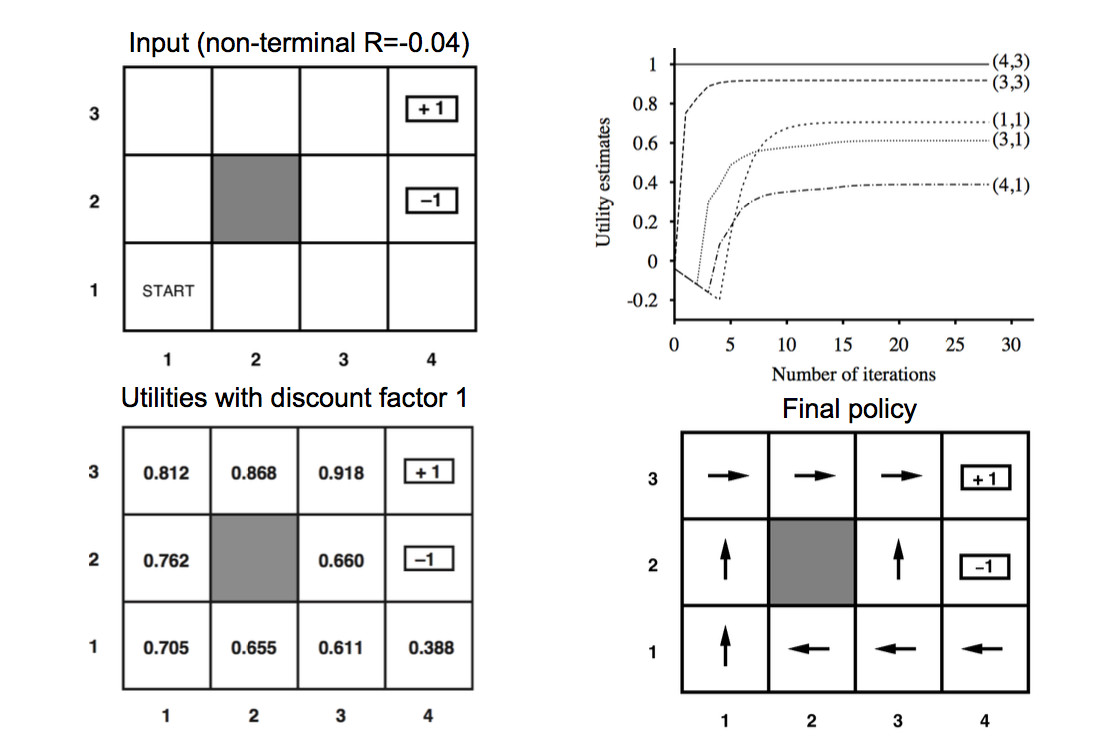from Abeel and Klein at Berkeley

From these utility values, we can read off a final policy (bottom right) using the equation

$\pi(s) = \text{argmax}_a \sum_{s'} P(s' | s,a) U_i(s')$

Value iteration eventually converges to the solution. Notice that the optimal utility values are uniquely determined, but there may be one policy consistent with them.

Policy iteration

Policy iteration produces the same solution, but faster. It operates as follows:

• Start with an initial guess for policy $\pi$.
• Alternate two steps:
  • Policy evaluation: use policy $\pi$to estimate utility values U
  • Policy improvement: use utility values U to calculate a new policy $\pi$

The values for U and $\pi$ are closely coupled. Policy iteration makes the emerging policy values explicit, so they can help guide the process of refining the utility values.

We saw above how to calculat an optimal policy from the utility values for all states. So we need to understand how to do the first (policy evaluation) step.

Utility from estimated policy

Our Bellman equation (below) finds the value corresponding to the best action we might take in state s.

$U(s) = R(s) + \gamma \max_a \sum_{s'} P(s' | s,a)U(s')$

However, in policy iteration, we already have a draft policy. So we do a similar computation but assuming that we will command action $\pi(s)$.

$U(s) = R(s) + \gamma \sum_{s'} P(s' | s, \pi(s)) U(s')$

We have one of these equations for each state s. The simplification means that each equation is linear. So we have two options for finding a solution:

• linear algebra
• a few iterations of value estimation

The value estimation approach is usually faster. We don't need an exact (fully converged) solution, because we'll be repeating this calculation each time we refine our policy $\pi$.

Asynchromous dynamic programming

One useful weak to solving Markov Decision Process is "asynchronous dynamic programming." In each

In each iteration, it's not necessary to update all states. We can select only certain states for updating. E.g.

• states frequently seen in some application (e.g. a game)
• states for which the Bellman equation has a large error (i.e. compare values for left and right sides of the equation)

The details can be spelled out in a wide variety of ways.

Intro to reinforcement learning

Reinforcement learning (RL) involves the same basic mathematical setup. However, our learning agent doesn't know P or R. So the agent has to start taking actions with incomplete (initially almost no) information, hoping to gradually learn how to perform well. We typically imagine that it does a very long sequence of actions, returning to the same state multiple types. There is no permanent end state, so hazards or losses send it back to some initial state.

A reinforcement learner may be

• Online: interacting directly with the world or
• Offline: interacting with a simulation of some sort.

The latter would be safer for situations where the hazards could cause real damage.

An important hybrid is "experience replay." In this case, we have an online learner. But instead of forgetting its old experiences, it will

• remember old training sequences,
• spend some training time replaying these experiences rather than taking new actions in the world

This is a way to make the most use of training experiences that could be limited by practical considerations, e.g. slow and/or costly.

The reinforcement learning loop

A reinforcement learner repeats the following sequence of steps:

• take an action
• observe the outcome (state and reward)
• update internal representation

There are two basic choices for the "internal representation":

• Model-based: estimate values for P(s'|s,a) and R(s)
• Model-free: estimate "Q" values, which sidestep the need to estimate P and R

We'll look at model-free learning next lecture.

Model-based RL

A model based learner operates much like a naive Bayes learning algorithm, except that it has to start making decisions as it trains. Initially it would use some default method for picking actions. As it moves around taking actions, it tracks counts for what rewards it got in different states and what state transitions resulted from its commanded actions. Periodically it uses these counts to

• Estimate P(S' | s,a) and R(s), and then.use these values to
• Estimate U(s) and $\pi(s)$ as above.

Adding exploration

This obvious implementation of a model-based learner is risk-averse. Once a clear policy starts to emerge, it has a strong incentive to stick to its familiar strategy rather than exploring the rest of its environment. So it could miss very good possibilities (e.g. large rewards) if it didn't happen to see them early.

To improve performance, we modify our method of selecting actions:

• with probability p, pick $\pi(s)$
• with probability 1-p, explore

"Explore" could be implemented in various ways, such as

• make a uniform random choice among the actions
• try actions that we haven't tried "enough" times in the past

The probability of exploring would typically be set high at the start of learning and gradually decreased, allowing the agent to settle into a specific final policy.