CS440/ECE448 Fall 2018
Assignment 7: Pong and Reinforcement Learning
Deadline: Monday, December 10th
Contents
- Problem Statement: Pong
- Part 1: Single-Player Pong
- Part 2: Two-Player Pong
- Extra Credit Suggestions
- Provided Code Skeleton
- Submission Instructions
Pong
In 1972, the game of Pong was released by Atari. Despite its simplicity, it was a ground-breaking game in its day, and it has been credited as having helped launch the video game industry. In this assignment, you will train AI agents using reinforcement learning to play a simple version of the game pong. You will implement a TD version of the Q-learning algorithm.
Image from Wikipedia
Provided Pong Environment
In this assignment, we have provided you with a basic pong environment for your agent to play in. The environment supports single-player pong and multi-player pong against a basic hard-coded opponent agent.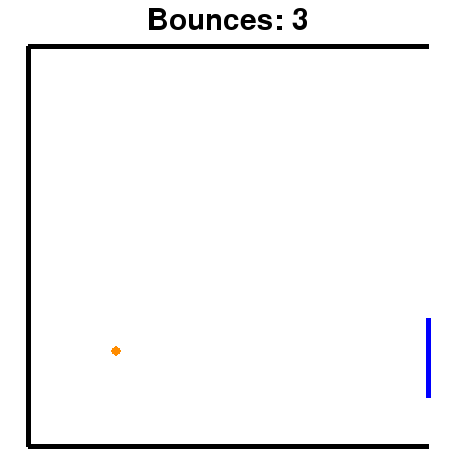
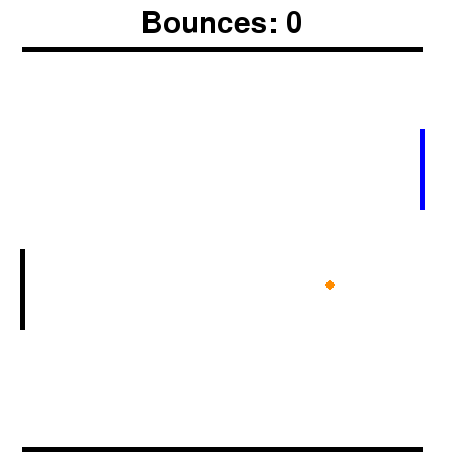
Single-player Pong and Multi-player pong
Pong as a Markov Decision Process (MDP)
Before implementing the Q-learning algorithm, we must first define Pong as a Markov Decision Process (MDP):- State: A tuple (ball_x, ball_y, velocity_x, velocity_y, paddle_y).
- ball_x and ball_y are real numbers on the interval [0,1]. The lines y=0 and y=1 are walls. The ball bounces off a wall whenever it hits. The line x=1 defended by your paddle. In the case of single-player pong, x=0 is also a wall. In the case of two-player pong, x=0 is defended by the opponent agent.
- The absolute value of velocity_x is at least 0.03, guaranteeing that the ball is moving either left or right at a reasonable speed.
- paddle_y represents the top of the paddle and is on the interval [0, 1 - paddle_height], where paddle_height = 0.2, as can be seen in the image above. The x-coordinate of the paddle is always paddle_x=1.
- Actions: Your agent's actions are chosen from the set {nothing, up, down}. In other words, your agent can either move the paddle up, down, or make it stay in the same place. If the agent tries to move the paddle too high, so that the top goes off the screen, simply assign paddle_y = 0. Likewise, if the agent tries to move any part of the paddle off the bottom of the screen, assign paddle_y = 1 - paddle_height.
- Rewards: +1 when your action results in rebounding the ball with your paddle, -1 when the ball has passed your agent's paddle, or 0 otherwise.
- Initial State: The ball starts in the middle of the screen moving towards your agent in a downward trajectory. Your paddle starts in the middle of the screen.
- Termination: For single-player pong, a state is terminal if the ball's x-coordinate is greater than that of your paddle, i.e., the ball has passed your paddle and is moving away from you. For two-player pong, a state can also be terminal if the ball has moved past the opponent agents paddle.
- Treat the entire board as a 12x12 (X_BINS x Y_BINS) grid, and let two states be considered the same if the ball lies within the same cell in this table. Therefore there are 144 possible ball locations.
- Discretize the X-velocity of the ball to have only 2 (V_X) possible values: +1 or -1 (the exact value does not matter, only the sign).
- Discretize the Y-velocity of the ball to have only 3 (V_Y) possible values: +1, 0, or -1. It should map to Zero if |velocity_y| < 0.015.
- Finally, to convert your paddle's location into a discrete value, use the following equation: discrete_paddle = floor(12 * paddle_y / (1 - paddle_height)). In cases where paddle_y = 1 - paddle_height, set discrete_paddle = 11. As can be seen, this discrete paddle location can take on 12 (PADDLE_LOCATIONS) possible values.
- Therefore, the total size of the state space for this problem is (144)(2)(3)(12) = 10369.
Part 1: Single-Player Pong

In this part of the assignment, you will implement a Q-learning agent that learns how to bounce the ball off the paddle as many times as possible in the single-player pong environment. In order to do this, you must use Q-learning. Implement a table-driven Q-learning algorithm and train it on the MDP outlined above. Train it for as long as you deem necessary, counting the average number of times your agent can get the ball to bounce off its paddle before missing the ball. Your agent should at least be able to rebound the ball at least nine consecutive times before missing it, although your results may be significantly better than this (as high as 12-14). In order to achieve an optimal policy, you will need to adjust the learning rate, α, the discount factor, γ, and the settings that you use to trade off exploration vs. exploitation.
After completing training, your algorithm should be able to average over 9 bounces on a set of (≥1000) testing games
Tips
- To get a better understanding of the Q learning algorithm, read section 21.3 of the textbook.
- Initially, all the Q value estimates should be 0.
- For choosing a discount factor, try to make sure that the reward from the previous rebound has a limited effect on the next rebound. In other words, choose your discount factor so that as the ball is approaching your paddle again, the reward from the previous hit has been mostly discounted.
- The learning rate should decay as C/(C+N(s,a)), where N(s,a) is the number of times you have seen the given the state-action pair and C is a constant that you must choose.
- To learn a good policy, you need on the order of 100K games, which should take just a few minutes in a reasonable implementation.
- For exploration versus exploitation, you should consider using either an epsilon greedy strategy or the exploration function defined in Chapter 21 of the textbook.
Part 2: Two-Player Pong

In this part of the assignment, you will implement a Q-learning agent that learns how to beat a hard-coded opponent agent. The hard-coded opponent agent simply follows the y coordinate of the ball up and down as it moves. You must follow the same approach as part 1, but you can change the parameters of the implementation. You can explore changing the exploration technique, the learning rate, or the reward function.
After completing training, your algorithm should win 50 percent of games against the opponent agent on a set of (≥1000) testing games
Extra Credit Suggestions
Extra credit is open ended on this assignment. Feel free to experiment with any approaches to improve performance of the agent in the pong environment. Please submit a report if you do extra credit. Below are a few suggestions:- Try changing how the environment is discretized to improve performance.
- Try using deep reinforcement learning approaches such as Deep Q-learning.
- Try using policy iteration or policy gradient methods.
- Try to get as many bounces as you can in the single player environment using a machine learning technique.
Provided Code Skeleton
We have provided ( tar zip) all the code to get you started on your MP, which means you will only have to implement the logic behind the q learning algorithm and discretizing the state.
- pong.py - This is the file that defines the pong environment and creates the GUI for the game.
- utils.py - This is the file that defines some of the discretization constants as defined above and contains the functions to save and load models.
-
agent.py This is the file where you will be doing all of your work. This file contains the Agent class. This is the agent you will implement to act in the pong environment. Below is the list of instance variables and functions in the Agent class.
- self._train: This is a boolean flag variable that you should use to determine if the agent is in train or test mode. In train mode, the agent should explore and exploit based on the Q table. In test mode, the agent should purely exploit and always take the best action.
- train(): This function sets the self._train to be True. This is called before the training loop is run in mp7.py
- test(): This function sets the self._train to be False. This is called before the testing loop is run in mp7.py
- save_model(): This function saves the self.Q table. This is called after the training loop in mp7.py.
- load_model(): This function loads the self.Q table. This is called before the testing loop in mp7.py.
- act(state, bounces, done, won): This is the main function you will implement and is called repeatedly by mp7.py while games are being run. "state" is the state of the pong environment and is a list of floats. "bounces" is the number of times the ball has bounced off of your paddle. "done" is a boolean indicating if the game is over. "won" is a boolean indicating if you have won the game (this will only ever be True in two-player pong). "bounces", "done", and "won" should be used to define your reward function.
act should return a number from the set of {-1,0,1}. Returning -1 will move the agent down, returning 0 will keep the agent in its current location, and returning 1 will move the agent up. If self._train is True, this function should update the Q table and return an action. If self._train is False, the agent should simply return the best action based on the Q table.
- mp7.py - This is the main file that starts the program. This file runs the pong game with your implemented agent acting in it. The code runs a number of training games, then a number of testing games, and then displays example games at the end.
To understand more about how to run the MP, run python3 mp7.py -h in your terminal.
General guidelines and submission
Basic instructions are the same as in MP 1. To summarize:
- For general instructions, see the main MP page and the course policies.
- We will do some code testing, but it may not be exhaustive.
This MP will not require a report. So, we're largely grading on performance. We will be grading based on your changes to agent.py so make sure that no other file is changed when you save and load your models. If you want to get extra credit, you can make changes to utils.py but remember your original models that you submit should use the unmodified utils.py You should submit on moodle:
- A copy of agent.py containing all your new code.
- A numpy array called model1.npy containing the saved Q matrix for single-player pong. (Can be saved by passing "--model_name model1.npy" to mp7.py )
- A numpy array called model2.npy containing the saved Q matrix for two-player pong. (Can be saved by passing "--model_name model2.npy" to mp7.py )
- Note that both the models above should work without modifying the utils.py. Please make sure that loading the model works with the default utils.py before submitting.
- (Groups only) Statement of individual contribution.
- (Bonus credit only) Brief statement of extra credit work (formatted pdf).
- (Bonus credit only) Modified utils.py. Submit models that use a modified utils.py with a prefix of model_ec.
This time, we're having everyone submit as a "group," so you'll need to create a single-person group if you're working alone.
Extra credit may be awarded for going beyond expectations or completing the suggestions below. Notice, however, that the score for each MP is capped at 110%.