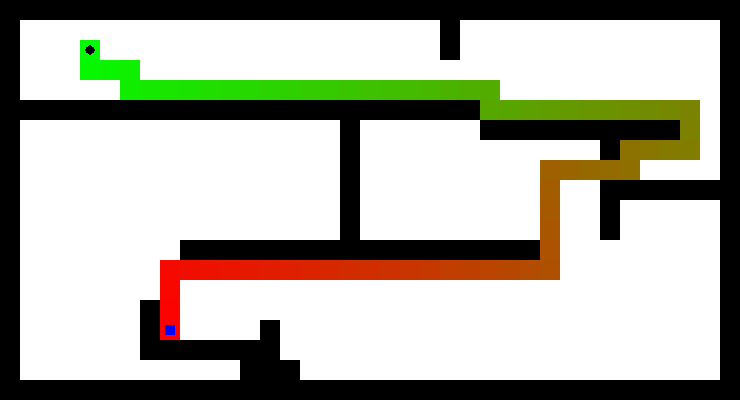
CS440/ECE448 Fall 2018

Assignment 1: Search

Due date: Monday September 24th, 11:55pm

Credits: Berkeley CS188 Pacman projects
Updated By: Micky Abir, Chris Benson, Krishna Kothapalli, and JD Lee

In this assignment, you will build general-purpose search algorithms and apply them to solving puzzles. In Part 1, you will be in charge of a "Pacman" agent that needs to find paths through mazes to eat a dot or "food pellets." In Part 2 you will need to find a single path that goes through all the dots in the maze.

See the the main MP page for programming language requirements, policies about working in groups, submission procedures, etc. Also make sure you are familiar with the course policies on academic integrity, late submissions, etc.

Contents

Part 1: Basic Pathfinding

Consider the problem of finding the shortest path from a given start state while eating one or more dots or "food pellets." The image at the top of this page illustrates the simple scenario of a single dot, which in this case can be viewed as the unique goal state. The maze layout will be given to you in a simple text format, where '%' stands for walls, 'P' for the starting position, and '.' for the dot(s) (see sample maze file). All step costs are equal to one.

Implement the state representation, transition model, and goal test needed for solving the problem in the general case of multiple dots. For the state representation, besides your current position in the maze, is there anything else you need to keep track of? For the goal test, keep in mind that in the case of multiple dots, the Pacman does not necessarily have a unique ending position. Next, implement a unified top-level search routine that can work with all of the following search strategies, as covered in class and/or the textbook:

  • Depth-first search
  • Breadth-first search
  • Greedy best-first search
  • A* search
For this part of the assignment, use the Manhattan distance from the current position to the goal as the heuristic function for greedy and A* search.

Run each of the four search strategies on the following inputs:

The provided code will generate a pretty picture of your solution. Your report should include

  • The solution picture.
  • The length of the path. Include both the start and goal positions as part of your path and path length.
  • Number of nodes expanded by the search algorithm.

Part 2: Search with multiple dots

Now consider the harder problem of finding the shortest path through a maze while hitting multiple dots. Once again, the Pacman is initially at P, but now there is no single goal position. Instead, the goal is achieved whenever the Pacman manages to eat all the dots. Once again, we assume unit step costs.

As instructed in Part 1, your state representation, goal test, and transition model should already be adapted to deal with this scenario. The next challenge is to solve the following inputs using A* search using an admissible heuristic designed by you:

You should be able to handle the tiny search using uninformed BFS. In fact, it is a good idea to try that first for debugging purposes, to make sure your representation works with multiple dots. However, to successfully handle all the inputs, it is crucial to come up with a good heuristic. For full credit, your heuristic should be admissible and should permit you to find the solution for the medium search in a reasonable amount of time. In your report, explain the heuristic you chose, and discuss why it is admissible and whether it leads to an optimal solution.

For each maze, your report should include (as for Part 1) the solution picture, the solution cost, and the number of nodes expanded in your search.

Extra Credit Suggestion

Sometimes, even with A* and a good heuristic, finding the optimal path through all the dots is hard. In these cases, we'd still like to find a reasonably good path, quickly. Write a suboptimal search algorithm that will do a good job on this big maze. Your algorithm could either be A* with a non-admissible heuristic, or something different altogether. In your report, discuss your approach and output the solution cost and number of expanded nodes.

Provided Code Skeleton

We have provided ( tar file or zip file) all the code to get you started on your MP, which means you will only have to write the search functions. Do not modify provided code. You will only have to modify search.py.

maze.py

  • getStart() :- Returns a tuple of the starting position, (row, col)
  • getObjectives() :- Returns a list of tuples that correspond to the dot positions, [(row1, col1), (row2, col2)]
  • isValidMove(row, col) :- Returns the boolean True if the (row, col) position is valid. Returns False otherwise.
  • getNeighbors(row, col) :- Given a position, returns the list of tuples that correspond to valid neighbor positions. This will return at most 4 neighbors, but may return less.

search.py

There are 4 methods to implement in this file, namely bfs(maze), dfs(maze), greedy(maze), and astar(maze). (You may need to add another named search method if you implement an additional search method for extra credit.) Each of these functions takes in a maze instance, and should return both the path taken (as a list of tuples) and the number of states explored. The maze instance provided will already be instantiated, and the above methods will be accessible.

To understand how to run the MP, read the provided README.md or run python3 mp1.py -h into your terminal. The following command will display a maze and let you create a path manually using the arrow keys.

python3 mp1.py --human maze.txt

The following command will run your astar search method on the maze.

python3 mp1.py --method astar maze.txt

You can also save your output picture as a file in tga format. If your favorite document formatter doesn't handle tga, tools such as gimp can convert it to other formats (e.g. jpg).

Tips

  • In your implementation, make sure you get all the bookkeeping right. This includes handling of repeated states (in particular, what happens when you find a better path to a state already on the frontier) and saving the optimal solution path. These topics have been extensively covered during the lectures.

  • Pay attention to tiebreaking. If you have multiple nodes on the frontier with the same minimum value of the evaluation function, the speed of your search and the quality of the solution may depend on which one you select for expansion.

  • Implement all four strategies using a similar approach and coding style. In particular, while DFS can be implemented very compactly using recursion, you must store the frontier in an explicit stack for this assignment. Among other things, limits on recursion depth can be (depending on your installation) much lower than the number of objects that you can pack into an explicit stack.

  • You will be graded primarily on the correctness of your solution, not on the efficiency and elegance of your data structures. For example, we don't care whether your priority queue or repeated state detection uses brute-force search, as long as you end up expanding (roughly) the correct number of nodes and find the optimal solution. So, feel free to use "dumb" data structures as long as it makes your life easier and still enables you to find the solutions to all the inputs in a reasonable amount of time.

Deliverables

Moodle submission instructions will be posted on the the main MP page. You will be uploading three files

  • Your report (pdf).
  • A copy of search.py containing all your new code.
  • (Groups only) Statement of individual contribution.

The statement of individual contribution is a brief summary of which group member was responsible for which parts of the solution and submitted material. We reserve the right to contact group members individually to verify this information.

Report Checklist

Your report should briefly describe your implemented solution and fully answer the questions for every part of the assignment. Your description should focus on the most "interesting" aspects of your solution, i.e., any non-obvious implementation choices and parameter settings, and what you have found to be especially important for getting good performance. Feel free to include pseudocode or figures if they are needed to clarify your approach. Your report should be self-contained and it should (ideally) make it possible for us to understand your solution without having to run your source code.

WARNING: You will not get credit for any solutions that you have obtained, but not included in your report! For example, you will lose points if your code prints out path cost and number of nodes expanded on each input, but you do not put down the actual numbers in your report.

Your report must be a formatted pdf document. Pictures and example outputs should be incorporated into the document. Exception: items which are very large or unsuitable for inclusion in a pdf document (e.g. videos or animated gifs) may be put on the web and a URL included in your report.

For full credit, in addition to the algorithm descriptions, your report should include the following.

Part 1: Basic Pathfinding

For every algorithm in part 1 (DFS, BFS, Greedy, A*) and every one of the three mazes (medium, big, open): give the maze with the computed path, the solution cost, and the number of expanded nodes (12 cases total).

Part 2: Search with multiple dots

For part 2, for each of the three mazes (tiny, small, medium): give the solution path, solution cost, and number of expanded nodes for your A* algorithm. Discuss your heuristic, including why it is admissibile.

Extra credit:

We reserve the right to give bonus points for any advanced exploration or especially challenging or creative solutions that you implement. This includes, but is not restricted to, the extra credit suggestion given above.