Processing math: 28%
Back to References


Graphs and Sparse Matrices

Learning Objectives

Links and Other Content

Nothing here yet.

Graphs

Undirected Graphs: The following is an example of an undirected graph:

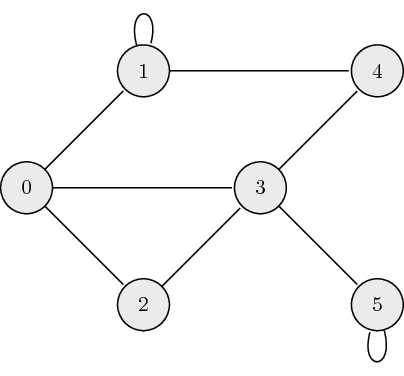
The adjacency matrix, A, for undirected graphs is always symmetric and is defined as: aij={1if (nodei,nodej) are connected0otherwise, where aij is the (i,j) element of A. The adjacency matrix which describes our example graph is: A=[011100110010100100101011010100000101].

Directed Graphs: The following is an example of a directed graph:

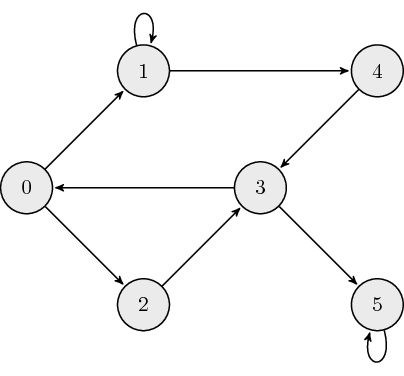
The adjacency matrix, A, for directed graphs is defined as: aij={1if nodei←nodej0otherwise, where aij is the (i,j) element of A. The adjacency matrix which describes our example graph is: A=[000100110000100000001010010000000101].

Weighted Directed Graphs: The following is an example of a weighted directed graph:

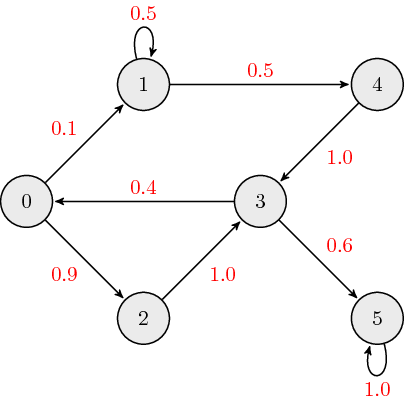
The adjacency matrix, A, for weighted directed graphs is defined as: aij={wijif nodei←nodej0  otherwise, where aij is the (i,j) element of A, and wij is the link weight associated with edge connecting nodes i and j. The adjacency matrix which describes our example graph is: A=[0000.4000.10.500000.900000001.001.0000.500000000.601.0]. Typically, when we discuss weighted directed graphs it is in the context of transition matrices for Markov chains where the link weights across each column sum to 1.

Markov Chain

A Markov chain is a stochastic model where the probability of future (next) state depends only on the most recent (current) state. This memoryless property of a stochastic process is called Markov property. From a probability perspective, the Markov property implies that the conditional probability distribution of the future state (conditioned on both past and current states) depends only on the current state.

Markov Matrix

A Markov/Transition/Stochastic matrix is a square matrix used to describe the transitions of a Markov chain. Each of its entries is a non-negative real number representing a probability. Based on Markov property, next state vector \boldsymbol{x}_{k+1} is obtained by left-multiplying the Markov matrix M with the current state vector \boldsymbol{x}_k. \boldsymbol{x}_{k+1} = M \boldsymbol{x}_k In this course, unless specifically stated otherwise, we define the transition matrix M as a left Markov matrix where each column sums to 1.

Note: Alternative definitions in outside resources may present M as a right markov matrix where each row of M sums to 1 and the next state is obtained by right-multiplying by M, i.e. \boldsymbol{x}_{k+1}^\top = \boldsymbol{x}_k^\top M.

A steady state vector \boldsymbol{x}^* is a probability vector (entries are non-negative and sum to 1) that is unchanged by the operation the Markov matrix M, i.e. M \boldsymbol{x}^* = \boldsymbol{x}^* Therefore, the steady state vector \boldsymbol{x}^* is an eigenvector for the eigenvalue \lambda=1 of matrix M. If there is more than one eigenvector with \lambda=1, then a weighted sum of the corresponding steady state vectors will also be a steady state vector. Therefore, the steady state vector of a Markov chain may not be unique and could depend on the initial state vector.

Markov Chain Example

Suppose we want to build a Markov Chain model for weather predicting in UIUC during summer. We observed that:

The state diagram is shown below:

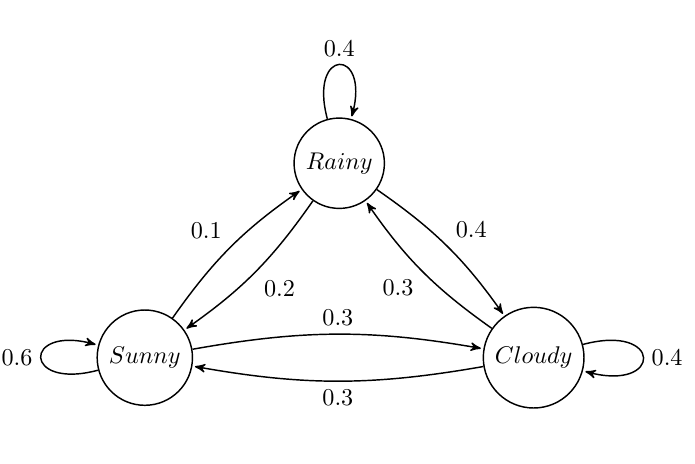
The Markov matrix is M = \begin{bmatrix} 0.6 & 0.2 & 0.3 \\ 0.1 & 0.4 & 0.3 \\ 0.3 & 0.4 & 0.4 \end{bmatrix}.

If the weather on day 0 is known to be rainy, then \boldsymbol{x}_0 = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}; and we can determine the probability vector for day 1 by \boldsymbol{x}_1 = M \boldsymbol{x}_0. The probability distribution for the weather on day n is given by \boldsymbol{x}_n = M^{n} \boldsymbol{x}_0.

Dense Matrices

A n \times n matrix is called dense if it has O(n^2) non-zero entries. For example: A = \begin{bmatrix} 1.0 & 2.0 & 3.0 \\ 4.0 & 5.0 & 6.0 \\ 7.0 & 8.0 & 9.0 \end{bmatrix}.

DNS (Dense Format) stores the matrix dimensions followed by the data values in row major order. For A the DNS format is: AA = \begin{bmatrix} 3 & 3 & 1.0 & 2.0 & 3.0 & 4.0 & 5.0 & 6.0 & 7.0 & 8.0 & 9.0 \end{bmatrix}.

Sparse Matrices

A n \times n matrix is called sparse if it has O(n) non-zero entries. For example: A = \begin{bmatrix} 1.0 & 0 & 0 & 2.0 & 0 \\ 3.0 & 4.0 & 0 & 5.0 & 0 \\ 6.0 & 0 & 7.0 & 8.0 & 9.0 \\ 0 & 0 & 10.0 & 11.0 & 0 \\ 0 & 0 & 0 & 0 & 12.0 \end{bmatrix}.

COO (Coordinate Format) stores arrays of row indices, column indices and the corresponding non-zero data values in any order. This format provides fast methods to construct sparse matrices and convert to different sparse formats. For A the COO format is: \textrm{data} = \begin{bmatrix} 12.0 & 9.0 & 7.0 & 5.0 & 1.0 & 2.0 & 11.0 & 3.0 & 6.0 & 4.0 & 8.0 & 10.0\end{bmatrix}, \\ \textrm{row} = \begin{bmatrix} 4 & 2 & 2 & 1 & 0 & 0 & 3 & 1 & 2 & 1 & 2 & 3 \end{bmatrix}, \\ \textrm{col} = \begin{bmatrix} 4 & 4 & 2 & 3 & 0 & 3 & 3 & 0 & 0 & 1 & 3 & 2 \end{bmatrix}.

CSR (Compressed Sparse Row) encodes rows offsets, column indices and the corresponding non-zero data values. This format provides fast arithmetic operations between sparse matrices, and fast matrix vector product. The row offsets are defined by the followign recursive relationship (starting with \textrm{rowptr}[0] = 0): \textrm{rowptr}[j] = \textrm{rowptr}[j-1] + \mathrm{nnz}(\textrm{row}_{j-1}), \\ where \mathrm{nnz}(\textrm{row}_k) is the number of non-zero elements in the k^{th} row. Note that the length of \textrm{rowptr} is n_{rows} + 1, where the last element in \textrm{rowptr} is the number of nonzeros in A. For A the CSR format is: \textrm{data} = \begin{bmatrix} 1.0 & 2.0 & 3.0 & 4.0 & 5.0 & 6.0 & 7.0 & 8.0 & 9.0 & 10.0 & 11.0 & 12.0 \end{bmatrix}, \\ \textrm{col} = \begin{bmatrix} 0 & 3 & 0 & 1 & 3 & 0 & 2 & 3 & 4 & 2 & 3 & 4\end{bmatrix}, \\ \textrm{rowptr} = \begin{bmatrix} 0 & 2 & 5 & 9 & 11 & 12 \end{bmatrix}.

CSR Matrix Vector Product Algorithm

The following code snippet performs CSR matrix vector product for square matrices:

import numpy as np
def csr_mat_vec(A, x):
  Ax = np.zeros_like(x)
  for i in range(x.shape[0]):
    for k in range(A.rowptr[i], A.rowptr[i+1]):
      Ax[i] += A.data[k]*x[A.col[k]]
  return Ax

Review Questions

  1. Given an undirected or directed graph (weighted or unweighted), determine the adjacency matrix for the graph.
  2. What is a transition matrix? Given a graph representing the transitions or a description of the problem, determine the transition matrix.
  3. For a problem modeled by a Markov matrix, what does a steady-state mean?
  4. Given an initial state, how can you use a transition matrix to determine the state (probability vector) after 1 timestep? After 2?
  5. For a Markov chain, what does the state at a given time step depend on?
  6. What properties must be true for a transition matrix?
  7. What does it mean for a matrix to be sparse?
  8. What factors might you consider when deciding how to store a sparse matrix? (Why would you store a matrix in one format over another?)
  9. Given a sparse matrix, put the matrix in CSR format.
  10. Given a sparse matrix, put the matrix in COO format.
  11. For a given matrix, how many bytes total are required to store it in CSR format?
  12. For a given matrix, how many bytes total are required to store it in COO format?

ChangeLog