Learning Objectives
In this lab you will learn about:
- Using a graph as a state space
- An introduction to reinforcement learning
Submission Instructions
Using the Prairielearn workspace, test and save your solution to the following exercises. (You are welcome to download and work on the files locally but they must be re-uploaded or copied over to the workspace for submission).
You will only need to modify the following files:
lab_ml.ipynb
Assignment Description
This lab tasks you with using NetworkX and your knowledge of graphs to ‘solve’ the game of Nim by repeatedly running paths through a graph.
For full credit here, you must implement:
- make_edge_list
- build_graph
- play_random_game
- update_edge_weights
The Game of Nim
The Game of Nim is a simple two player game with only a few rules:
- Each game starts with k tokens on the table
- Starting with Player 1, players alternate turns:
- Each turn, a player may pick up 1 or 2 tokens
- The player who picks up the last token (or tokens) wins
By default, the game usually starts with 10 tokens (k == 10). You should play a few rounds with your lab partner to get an understanding of the game.
Part 1: A State Space for Nim
A state space is a mathematical representation of the state of a physical system. In our case, the physical system is the game of Nim.
At the start of Nim(10), it is Player 1’s turn with 10 tokens available. We can label this state p1-10, for “Player 1 with 10 tokens available”. When Player 1 takes a token, the state is now p2-9 (or, if Player 1 takes two tokens, p2-8).
Each state is a vertex on a graph with directed edges connecting vertices when there is a valid move between the two states. Therefore, the state space with all the valid moves as edges makes the following graph:

The Nim State Space (as an edge list)
# INPUT:
# tokens, an integer for the total number of tokens
# OUTPUT:
# a list of edges that define the Nim graph
def make_edge_list(tokens):
Given an arbitrary number of tokens, create an edge list (as list of lists) defining the allowable state space of the Nim graph.
For full credit on the autograder, your output must adhere to the following exactly:
- Each vertex label is a string of the form
p<#>-<tokens>where<#>is either 1 or 2 and tokens is the number of tokens still in play. - Each edge in the list must be of type list (or tuple), where the first value is the start vertex label and the second value is the end vertex label.
- Edges are directed and exist only for valid moves.
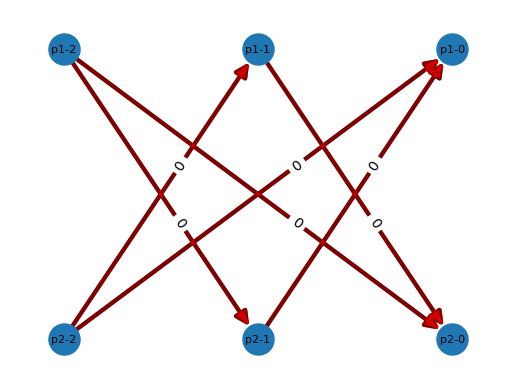
For example, if I had two tokens then the output would be:
[['p1-1', 'p2-0'],
['p1-2', 'p2-0'],
['p1-2', 'p2-1'],
['p2-1', 'p1-0'],
['p2-2', 'p1-0'],
['p2-2', 'p1-1']]
As we can see in this list, each player takes turns so p1 nodes only connect to p2 nodes. At the same time, each player can only take one or two tokens so we have direct edges from p1-2 to both p2-1 and p2-0.
Consider: Why does p1-1 and p2-1 only have a single outgoing edge?
Note: The order of the edges in an edge list dont matter but the content does!
The Nim State Space (as an NetworkX DiGraph())
# INPUT:
# edgeList, a list of lists storing the set of edges in the graph
# OUTPUT:
# a weighted, directed networkx graph (DiGraph) storing the input collection of edges, each with weight 0
def build_graph(edgeList):
Given a correct edge list produced by make_edge_list(), the next task is to build a NetworkX graph out of our input!
For full credit on the autograder, your output must adhere to the following exactly:
- The graph must be a directed graph. This means use
nx.DiGraph()as your graph object! - The graph must be weighted. To do this in NetworkX, you must create the attribute
weightand set its starting value to 0.
Hint: We saw several ways to create a graph in NetworkX. The easiest solution here is to add each edge one at a time using add_edge(). How can you add an edge with a ‘weight’ attribute to this function?
Successful completion of this function should allow you to visualize your graph using the provided plotGraph() function. For the above example (tokens = 2), the graph should look like:
Part 2: Nim Reinforcement Learning
One of the most classic methods of machine learning is reinforcement learning. In reinforcement learning, an algorithm is rewarded for making a good choice and punished for making a poor choice. After some training, the algorithm will have a better idea what choices are good and what choices are poor.
To apply reinforcement learning, we need a series of choices. In this lab, our algorithm will learn Nim through examining random paths through the game. For example, one random path Nim(10) is the following:
p1-10 ➜ p2-8 ➜ p1-7 ➜ p2-6 ➜ p1-4 ➜ p2-3 ➜ p1-1 ➜ p2-0
Visually:

Playing Nim (with 0 players)
# INPUT:
# G, a networkx graph storing a weighted graph of Nim states
# start, a string vertex label for the starting state of the game
# seed, an optional seed argument to make sure game play is consistent and autogradable
# OUTPUT:
# A list of game moves consisting of [start state, end state] edges
# At each node in the graph, the next move should be determined using random.choice
def play_random_game(G, start, seed=None):
Given a graph of directed edges and a start vertex, we can play a totally random game of Nim according to the following logic:
- At my current node, build a list of my next moves (adjacency nodes).
- Randomly pick one of my choices using
random.choice() - Record my choice by appending
[start, end]to an output list (my path) - Set my current node to the end state I have chosen.
- Repeat until I have no moves remaining (I am in state
p1-0orp2-0)
The function skeleton provided already handles the seed argument for you. You can test that your logic works using the provided examples (and the autograder).
Teaching a Machine to Learn
# INPUT:
# G, a networkx graph storing a weighted graph of Nim states
# path, a list of game moves consisting of [start state, end state, weight] triples
# OUTPUT:
# None, instead updates the weights of each path to add +1 to moves by the winner
# and add -1 to moves by the loser
def update_edge_weights(G, path):
Finally, we need to apply reinforcement learning. Given a path, we want to reward good decisions. We will define a good decision as all decisions made by the player who won. Therefore, if Player 1 took the last token (as in our example), all choices made by Player 1 is rewarded.
The reward is captured in our algorithm as the edge weight. When we consider a path through the graph, we can find the all edges along a path that has Player 1 winning (eg: the last vertex in the path goes to Player 2 with no tokens remaining, or “p2-0”, meaning that Player 1 took the last token), then all choices made by Player 1 (edges where Player 1 is the source vertex) are rewarded by increasing the edge weight by +1 and all choices made by Player 2 are punished by changing the edge weight by -1.
After one update, several edges will have a weight of 1, several edges will have a weight of -1, though most edges have not been visited and will have their initial weight of 0. After several thousand updates of random games, edges that result in more victories will have increasingly large edge weights.
TL;DR: Given a path through the Nim graph (output by play_random_game()), modify your Nim graph to increase the edges chosen by the winner by +1 and decrease the edges chosen by the loser by -1.
Hint 1: Given a path through the graph, how do I know the winner? Remember that the person who made the last move has won. Another way of saying the same thing is that ‘if my turn begins with 0 tokens left, I have lost the game’.
It may also help you to remember that list[-1] will return the last item in the list. :)
Hint 2: How can I update an attribute in NetworkX? If I have a NetworkX graph, I can access any specific edge attribute using the syntax:
G = nx.DiGraph() # Assume this is my graph
G[start][end][attribute]=value
So for example, if I had a attribute ‘weight’ and wanted to update the edge ['p1-1','p2-0'] (a winning move) I might say:
G['p1-1']['p2-0']['weight']+=1
Putting it Together
Once you have completed all functions, you can observe the output of your Nim algorithm using the provided code at the bottom of the lab notebook. Feel free to change the number of games or starting tokens (though I would not recommend setting tokens to be larger than 10).
Looking at the results, you should be able to answer several questions:
- When there’s exactly two tokens left, what should Player 1 do? (In other words, what are the edge weights of the out edges of
p1-2andp2-2?) - When there are four tokens left, what can Player 2 do? (In other words, what are the edge weights out of
p1-4andp2-4?) - Would you prefer to go first or second in a game of Nim?