Learning Objectives

• Implement fundamental graph file parser
• Conceptualize what a ‘greedy heuristic’ algorithm is.
• Practice traversing through a graph in a defined order
• Practice identifying a vertex’s neighbors using an adjacency matrix

Getting set up

From your CS 277 git directory, run the following:

git fetch release
git merge release/mp_color -m "Merging initial mp_color files"

You will find the relevant code and data as sub-folders within mp_color.

Assignment Description

UIUC is drafting up the final exam schedule for the next semester but they’ve decided that the best exam schedule is to simultaneously offer as many exams as possible (and to offer each exam only once). After all, if they can minimize the total number of exam ‘slots’ and just hire an abundance of support staff and proctors then they save money and students get a longer break so everyone wins right?

To determine the best schedule in an unbiased way, they plan to use graph coloring – a strategy which assigns a ‘color’ (in this context an exam time slot) to each vertex. The trick here is that the vertices are classes and edges are drawn between any two classes which has at least one student in common in their roster. In that way, by restricting the color labels such that all vertex colors are distinct from all their neighbors, UIUC can ensure that there is no conflicts in their exam scheduling.

Graph Coloring

Given a graph (G = V, E), a graph coloring is an assignment of labels to the vertices according to a context-dependent constraint. In the case of this lab, that constraint is that no two adjacent vertices are allowed to be the same color. This seemingly straightforward problem is actually an NP-complete problem. Given a list of colors for every vertex (a labeling), the correctness of a labeling can be determined very quicky but identifying the smallest number of ‘colors’ that we need to fully label a graph requires a brute-force search in polynomial time (O(n^k)).

In this lab, we will not attempt to brute force the solution and instead will rely on a greedy heuristic – an algorithm which is not guaranteed to find the optimal solution but will get us a valid solution quickly.

Part 1: Parse the input file

The input data format for this mp is a space-separated text file storing edges as the two vertices it connects. For example, the ‘file’:

CS277 CS296
CS180 CS181

implies that there is an edge between vertices CS277 and CS296 as well as an edge between CS180 and CS181. For this mp, we are going to store the graph as an adjacency matrix. However unlike in class, instead of inserting each vertex one at a time and resizing our matrix constantly, we will instead read in the graph with two passes over the same input file.

# INPUT:
# a string, inFile, giving the path to an input file
# OUTPUT:
# A sorted list of strings containing the vertex labels for all vertices
# NOTE: You can (and should) use built-in sort for strings
List[str] parseFile_vert(str inFile):

The first pass, parseFile_vert, should read through the entire file and build a list of the unique course IDs in the graph (all the vertices). Note that you should only include each class in the list of vertices once, even if the same class is found multiple times within the input file. The output list also MUST be sorted (as they are strings this will be lexicographically). However rather then require you to re-implement one of the many sorting strategies we’ve covered thus far, you are allowed to use built-in sort for this assignment.

# INPUT:
# a string, inFile, giving the path to an input file
# a list of vertex labels
# OUTPUT:
# A 2D matrix storing the edges between all vertices in the graph
# NOTE: The matrix order MUST match that of the input vartex labels
# (That is to say, matrix[0][1]) is the edge between vertex[0] and vertex[1]
# REMEMBER: Since our edges are undirected, matrix[x][y] should always equal matrix[y][x]!
List[List[bool]] parseFile_matrix(str inFile, List[str] vertices):

The second time you read through the file, you are building the adjacency matrix (all the edges). Your 2D matrix should be ordered according to the input list. For example if vertex[0]="CS277" and vertex[5]="CS131" then an edge between these two classes would be represented by matrix[0][5]=matrix[5][0]=1. Likewise if there is no edge between two classes, you would represent it by matrix[x][y]=matrix[y][x]=0. Note that because our edges are undirected, you should always be setting the two values [x][y] and [y][x]. (Technically we could represent this graph with only the upper diagonal but that is significantly more work for little conceptual gain).

Part 2: Order by degree

Given the vertex list and an adjacency matrix, you can now use the graphMatrix() class which contains useful helper functions for associating graph labels with index values (and vice versa). Use this class and these helper functions to write up two additional functions: getEdges() and areAdjacent().

# INPUT:
# A string, label, storing the vertex label being queried
# OUTPUT:
# The corresponding row in the adjacency matrix for the query
# The row will be a list of bools (0 or 1) of length equal to the number of vertices
List[bool] graphMatrix.getEdges(str label):

getEdges is an accessor function – we are often interested in looking up a vertex by its’ string label but the matrix stores its edges based on an index value. Your implementation here should take in the label, convert it into the corresponding index, and then return the list of edges associated with that vertex. Again because we are storing the full 2D matrix and not the upper diagonal, this is a fairly straightforward function so don’t overthink it! Your output should have one entry for every vertex in the graph.

# INPUT:
# A string, u, the label of one vertex being queried
# A string, v, the label of the other vertex being queried
# OUTPUT:
# A bool value indicating if vertices u and v are adjacent
bool graphMatrix.areAdjacent(str u, str v):

areAdjacent is another accessor function – given two vertex labels the function should convert the labels to integer indexes and lookup (and return) the corresponding entry in the adjacency matrix.

Part 3: Graph Coloring

# INPUT:
# A list of strings containing the vertex labels for all vertices
# OUTPUT:
# A list of ints containing the color label for all vertices
# The order of integers should match the order of strings. 
# (If inList[0]="Vertex1", then outList[0] should be Vertex1's color label.)
List[int] graphMatrix.colorGraph(List[str]):

As shown in chass, the graph coloring heuristic we are using is very simple – when at an unlabeled vertex, check all adjacent vertices for colors and pick the first color which does not belong to any neighbor. (When the neighbor vertex does not yet have a color, we can ignore it). This approach will not guarantee an optimal (or even very good) coloring scheme but if we enforce a specific order of vertices to visit, it will result in a consistent coloring scheme.

For example, if we ‘visit’ vertices in alphabetical order (A, B, C, D, E) then the heuristic will produce the following labeling (we often represent colors by numbers for convenience):

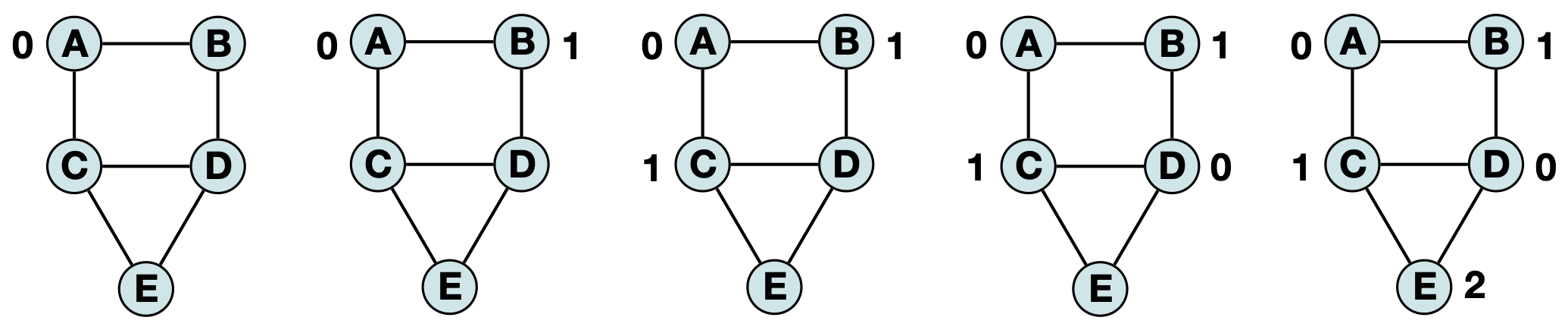
However, if we ‘visit’ vertices in based on the highest degree to lowest degree (C, D, A, B, E) we get a similar (but distinct) labeling:

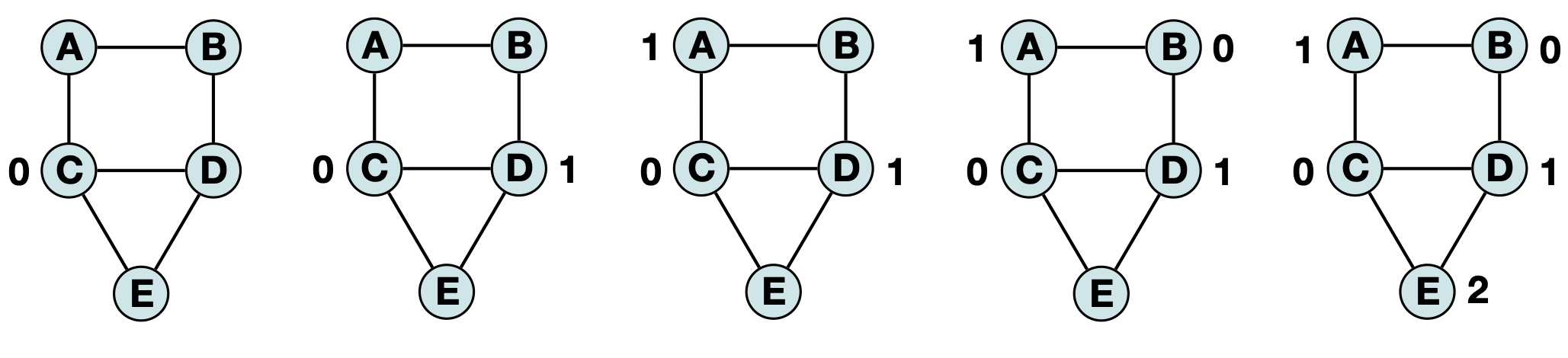
You should return a list based on the same order of the input vertices only containing an integer ‘color’ rather than a string label. Your function will be graded for an exact reproducibility of the color labeling for a given input but you should be aware that there are usually many valid colorings. In larger, more complex examples, this can result not just a different labeling but a different total number of colors. For the purposes of our motivating problem, we would likely run our heuristic several times on different inputs to try to approximate the smallest total set of colors is the number of unique exam slots we need to schedule all exams without any course conflicts. As this cannot be reasonably graded, I leave it as an exercise to the reader.

CONSIDER: To get the best possible solution, what is the first vertex we want to visit? What is the last possible vertex we want to visit? If you are interested, try out a few different vertex orderings and see if one consistently outperforms.