B-Trees
by Adrian ClarkDefinition
A B-Tree is a self balancing Binary Search Tree(BST). In this type of tree where each node can potentially have more than 2 children. Each node tends to hold 2 containers, in this case lets say 2 arrays, where one array holds the keys of the node and the other points to the children of the node.
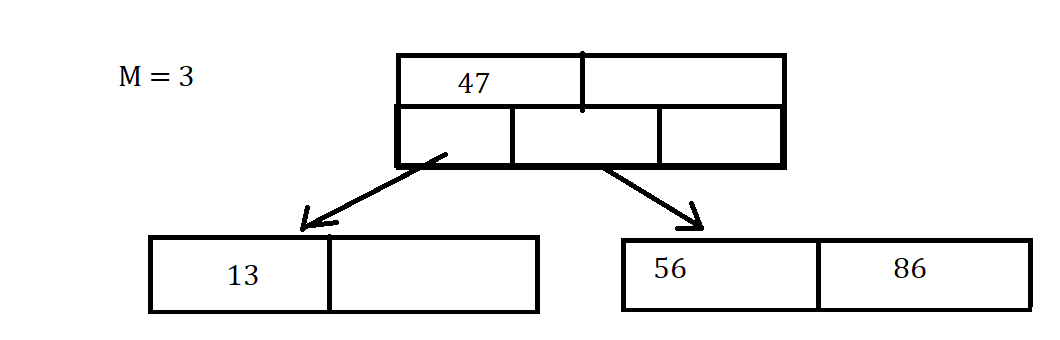
B-tree Properties
Here are some things to keep in mind about the properties of B-tree:
- M denotes the max number of child nodes a node can point to
- The max number of keys per node is M-1
- The root node is either a leaf node or an internal node with 2 to M children and 1 to M-1 Keys
- The rest of the internal nodes have between M/2 and M children
- All leaves are at the same depth, which makes the tree Balanced
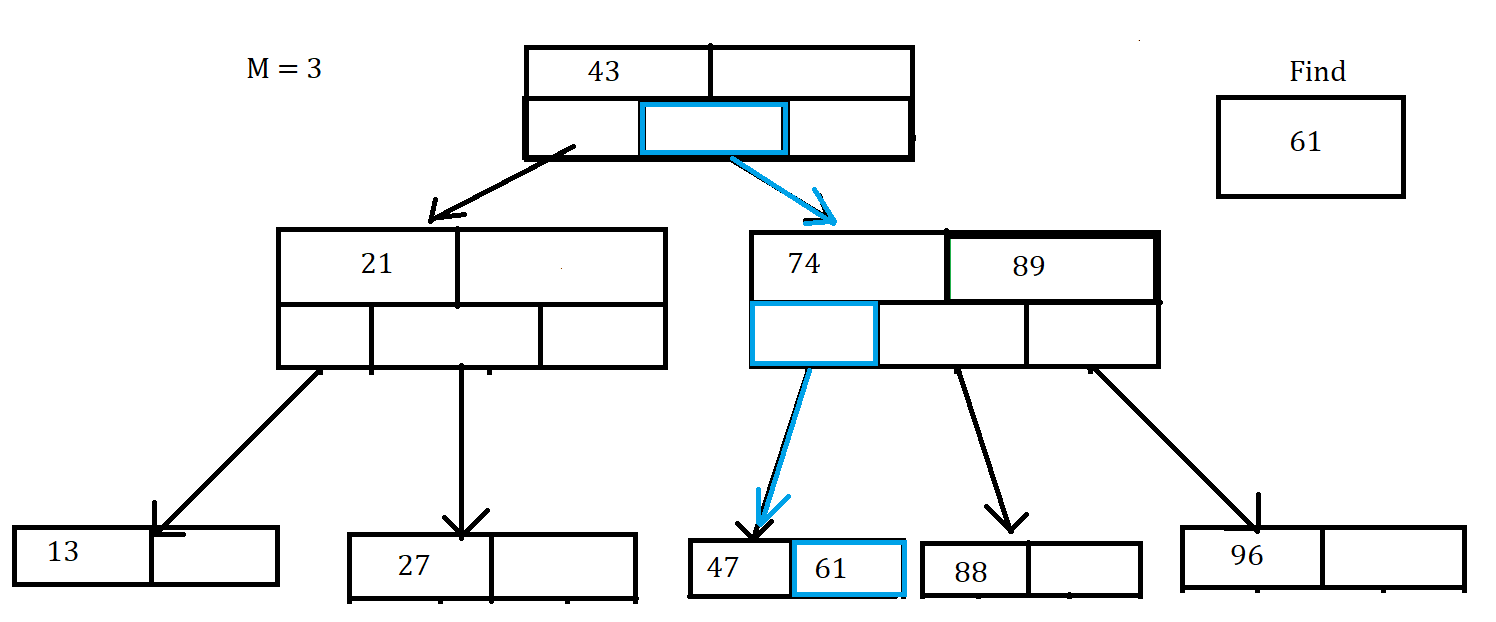
Find
The process of Finding a certain key is very similar to Searhcing in a BST, especially since B-trees are a type of BST. This is also another case where recursive traversal is preferred. For the Steps below, note that i represents the index of the key you are currently on.
Steps:
- Go through each index of the current node’s array of keys
- If the key is in this node’s array of keys, return the key
- If the key is not in this node you have two options.
One: Find the next biggest key and go to the ith child of that node, also known as the left child of the current key.
Two: Find the next smallest key and go the (ith + 1) child, also known as the right child of the current key. I say you have two options, as there is a potential for the key you are searching for to be less than the first key or greater than the last key of a Node.
- If you get to the leaf node where the data value should be and don’t see it in the array of keys then this value is not in the tree.
In this one we can see that we start in the root and follow the path of blue arrows and boxes to find the correct value. Even though it’s not shown in this picture,remember to go through the array of keys for the nodes you go through
Insertion
The process of inserting requires you navigate down to a leaf node by searching for a valid spot to insert the data. When you reach the bottom you will attempt to add the data. I say attempt, because if there is an open space in that node for the data it will be quick and simple. But this is not always the case, sometimes nodes are full and you will have to Split nodes.
Let’s say we want to Insert the key of 1337. Then we first have to find the correct node, and see if there is space for the Insertion of the data.
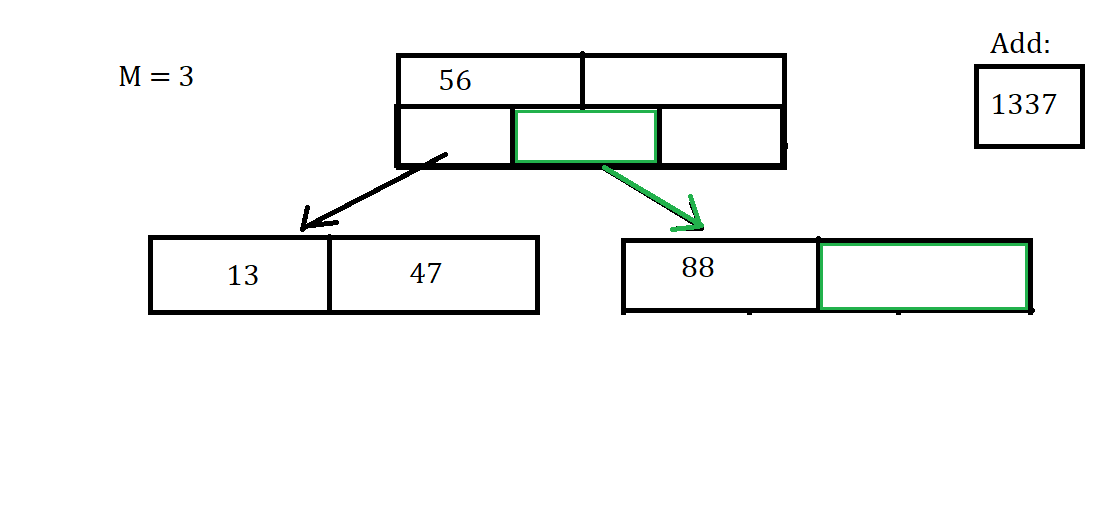
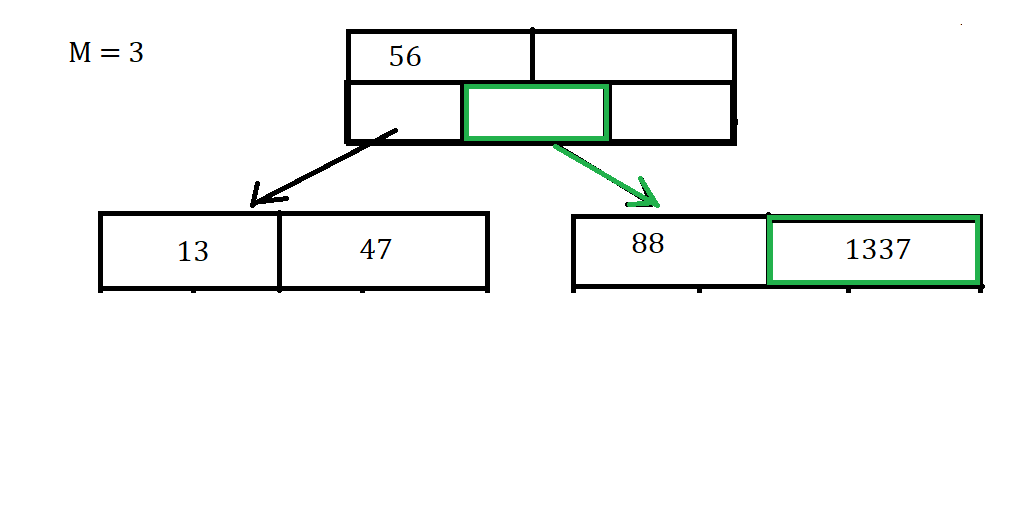
Luckily for us this is a very simple case and we can just directly insert the key into the node. This will not always be the case because we might have to Split a node, or shuffle the arrays of the node around to make sure they are in the correct order.
Splitting Nodes
Splitting nodes usually takes place after the insertion of a key.
Steps:
- When you try to insert into node, N1, you notice that the amount of keys is now greater than M-1.
- Now You must take the middle key and put it in the parent node’s keys
- Now all keys that were in the array of N1 that are greater than the thrown up key are put into a node that is the (i + 1), where i is the index of the thrown up key, child of the parent node. The rest are put into the Node that is the ith child of the parent tree. If a Node does not exist for that child but is a valid child to place ,Since there is space in the parent, you can create the child Node and populate it.
So let’s say we try to add the value 88 to a tree.
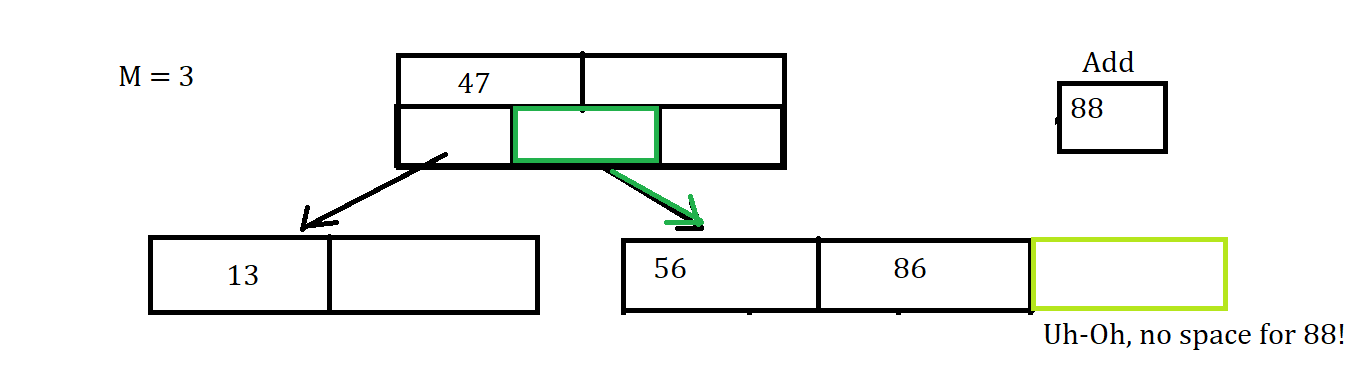
Uh-Oh that node is Full, So Now we have to throw the value of 86 up to the parent Node since it is the middle value, between the values of 56 and 88. Since that was the middle value thrown up and 88 is greater than 86, we put 88 into the (i+1) child node which was initially empty, where i is the index of 86 in the parent node.
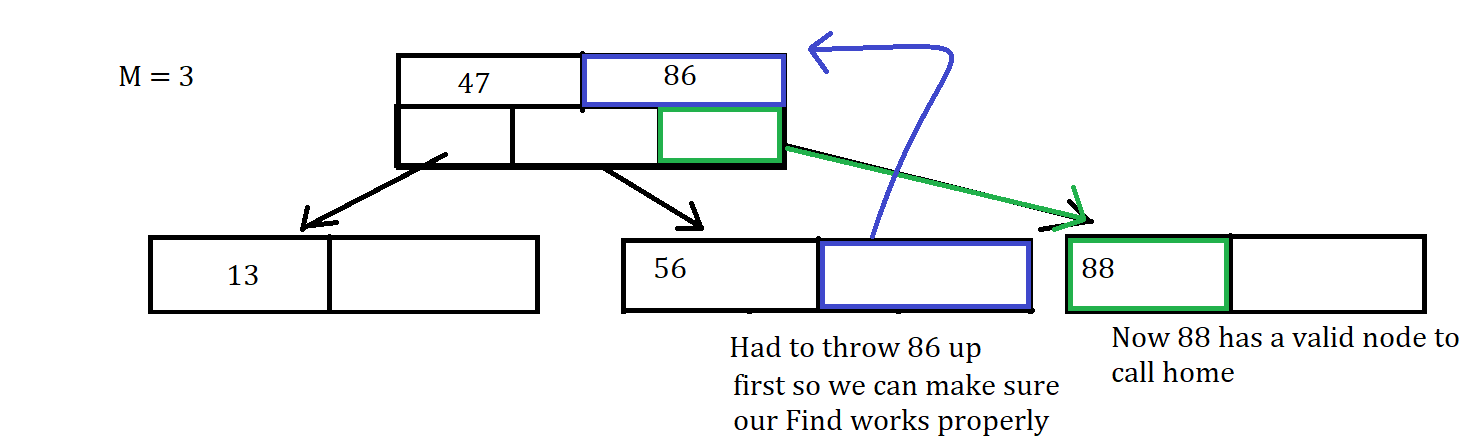
This is another case where we were lucky our operations were simple because you could run into the problem that the parent node is also full, requiring you to do more operations.
Removal/Deletion
Removal/Deletion of a data point is not done in Lab B-Tree
Removing is very similar to Inserting: you navigate down to the leaf node by searching and when you reach the key you have to delete the data. After you have deleted the data though, you have to make sure the tree still holds its BST property and the B-tree properties. Did that removal remove an important key in a Node? Did that removal make a Node fall below M/2 children? These are just examples of potential scenarios that come out of deletion, and this is where the idea of combining nodes comes in.
Let’s say we want to Remove the Data Value of 88. Then we first have to find the Node, if it exists, and remove it.
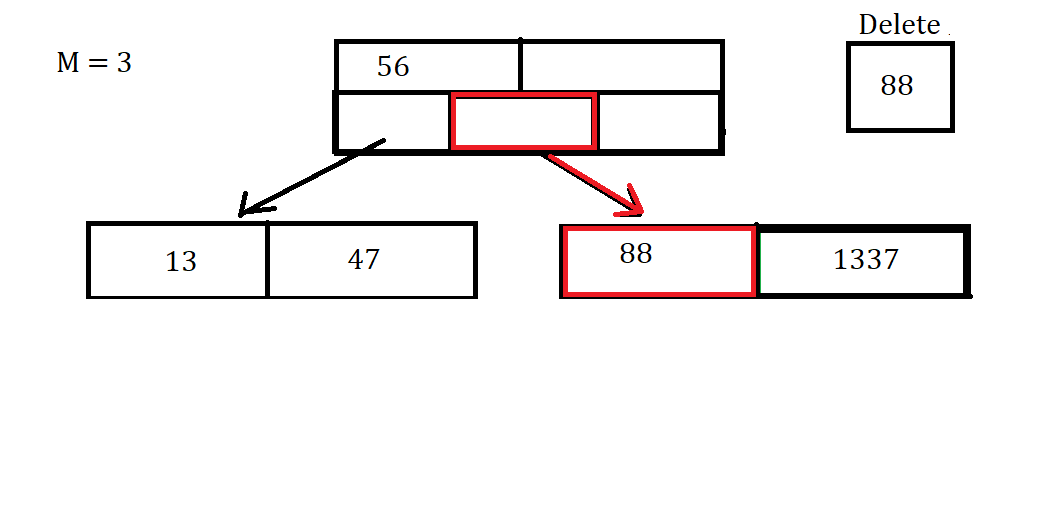
Once we’ve deleted that data point, You might notice that there is a gap in our array, which we don’t want. In order to combat this, we can move the data value 1337 into the spot previously held by 88.
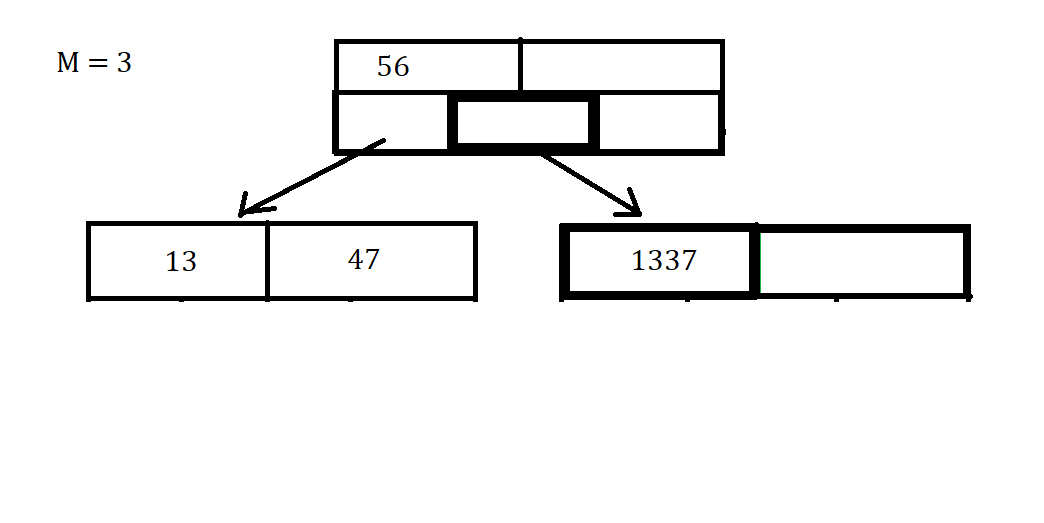
Luckily this Deletion didn’t make us have to combine any Nodes so it was a simple process this time. Deletion can be more complicated and you can visit here or take CS411 - Database Systems to learn more about Deletion because there are also different Merging scenarios that result from Deletion.
Merging Nodes
The Merging of Nodes of is not done in Lab B-Tree
Combining nodes usually takes place after the deletion of a key. For example, maybe after you removed the data, a node has less than M/2 children, then you must combine certain nodes.
The Merging of nodes is not as simple as Splitting due to the fact that you have to deal with more semantics of the tree. As you could be moving around multiple keys, and not just throwing them up to Parent Nodes but also throwing them down to various children nodes as well.
If you wish to learn more I encourage you to Google it or check out the link in the “Removal/Deletion” section of this page
Runtime
Search:
O(logn)
Since this is a BST and our search algorithm will have us checking each node for the value and if its not there we go to the correct child node, our run time is O(log(n)). Or more formally we can say the runtime is equal to O(depth*logM) where depth is equal to log(n), which, since N » m we can say is just O(log(n)) in the end.
Combining/Splitting of Keys:O(M) Since each Node can have up to M keys and we have to find the correct key to split/combine upon.
Insert/Delete: O((M/log M)*logN) Since we have to first go to the leaf node and find where to put the Node and now have to update the tree, by splitting and combining keys, in order to maintain the tree.