mp_schedule

Checking Out the Code

All assignments will be distributed via our release repo on github this semester. You will need to have set up your git directory to have our release as a remote repo as described in our git set up

You can merge the assignments as they are released into your personal repo with

git pull --no-edit --no-rebase release main
git push

if you are using multiple machines you may need to use the following to allow them to work correcly.

git pull --no-edit --no-rebase release main --allow-unrelated-histories
git push

The first git command will fetch and merge changes from the main branch on your remote repository named release into your personal. The --no-edit flag automatically generates a commit message for you, and the--no-rebase flag will merge the upstream branch into the current branch. Generally, these two flags shouldn’t be used, but are included for ease of merging assignments into your repo.

The second command will push to origin (your personal), which will allow it to track the new changes from release.

You will need to run these commands for every assignment that is released.

All the files for this mp are in the mp_schedule directory.

Preparing Your Code

This semester for MPs we are using CMake rather than just make. This allows for us to use libraries such as Catch2 that can be installed in your system rather than providing them with each assignment. This change does mean that for each assignment you need to use CMake to build your own custom makefiles. To do this you need to run the following in the base directory of the assignment. Which in this assignment is the mp_schedule directory.

mkdir build
cd build

This first makes a new directory in your assignment directory called build. This is where you will actually build the assignment and then moves to that directory. This is not included in the provided code since we are following industry standard practices and you would normally exclude the build directory from any source control system.

Now you need to actually run CMake as follows.

cmake ..

This runs CMake to initialize the current directory which is the build directory you just made as the location to build the assignment. The one argument to CMake here is .. which referes to the parent of the current directory which in this case is top of the assignment. This directory has the files CMake needs to setup your assignment to be build.

At this point you can in the build directory run make as described to build the various programs for the MP.

You will need to do the above once for each assignment. You will need to run make every time you change source code and want to compile it again.

Goals and Overview

In this MP you will:

• Create a program that acts as a file parser and data cleaner
• Design and implement a graph data structure of your choosing
• Design and implement a heuristic solution to graph coloring

Assignment Description

The primary task of this assignment is to create a functional graph representation of a mixture of student and course data.

• Part 1 — Data Parsing and Cleaning
• Part 2 — Graph Representation and storage
• Part 3 — Scheduling Exams

Unlike previous assignments, the autograder will only test part 1 and part 3. You have total freedom on how you produce a final schedule for the input data and any intermediate graph structures you create.

Part 1: Data Parsing Cleaning

For this first exercise, you are tasked with performing data parsing and cleaning to create 2D-arrays of strings (as two functions file_to_V2D and clean). All input files will be CSV-formatted which – if you are unfamiliar with CSV – stands for comma-separated-values file. In other words, your input will be of the form:

r0c0, r0c1, r0c2, r0c3
r1c0, r1c1, r1c2

You can assume that all entries will be well-formed, that is to say that there will always be an entry after each comma and a comma between every two entries.

# INPUT:
# A std::string containing the filename of the file being processed
# OUTPUT:
# A V2D containing the raw processed values in the file.
# Each individual item in the CSV must be stripped (trimmed) of whitespace and the order of rows and columns 
# must be preserved.
V2D file_to_V2D(const std::string & filename)

The first function file_to_V2D() will take in a filename as input and should return a V2D in which each element of the CSV is its own string entry in a 2D vector matrix. You must preserve the same order as the input file – so ‘r0c0’ in the above example would be found in V2D[0][0].

Several support functions have been provided in utils.h that – if used properly – can greatly simplify this task. These util functions (and the file reader) may be useful for the final project as well so be sure to understand how they operate! Also note that removing whitespace does not split ` Two Words ` into Two and Words but trims the potential whitespace on either side of the text. So you can use it freely without worrying that it will change the number of items by misinterpreting a single string as two.

# INPUT:
# A std::vector<std::vector<string>> (typedef V2D) containing roster information for each course
# A std::vector<std::vector<string>> (typedef V2D) containing course enrollment information for each student
# OUTPUT:
# A V2D containing corrected roster information for each course
#
# A student is 'correctly' in the class if both roster and course information support this
# A class is 'correctly' in the final roster if it has at least one valid student.
V2D clean(V2D & cv, V2D & student)

As with most data science projects, you cannot assume that the input data is entirely without errors. The second function for part 1, clean() tasks you with correcting (by removing) students who are either not registered for the class (as in they are not in the course roster information V2D for a specific class) or do not think they are enrolled in the course (as in they are not in the student’s own enrollment information in the student V2D). Lastly, if a course ends up not having any valid students, you should also remove the course from the final output V2D.

The output of this function should be a V2D in a roster-ordered format (valid courseIDs followed by a list of all valid students). As with file_to_V2D(), the order of the rows and columns (which have not been removed) must be consistent.

Example:

RosterFile:
CS101, a, b, c, d, e
CS102, a, b, c, f
CS103, a, b, c
CS104, z

StudentFile: 
a, CS101, CS102
b, CS101, CS102
c, CS101, CS103
e, CS102

Corrected RosterFile:
CS101, a, b, c
CS102, a, b
CS103, c

In this example, students d, f, and z don’t exist, student e is not a valid student for CS 101 (as it is not listed in both student and roster files), and that CS 104 does not actually have any valid students. In all cases, the invalid students and courses are removed from the final V2D.

Grading Information — Part 1

The following files are used to grade mp_schedule:

• src/schedule.cpp
• src/schedule.h

All other files including your testing files will not be used for grading.

Extra Credit Submission

For extra credit, you can submit the code you have implemented and tested for part one of mp_schedule. You must submit your work before the extra credit deadline as listed at the top of this page.

Part 2: Building an unweighted undirected graph

For this final MP, you have significant freedom in implementation details. In particular, there is no required class or function for constructing a graph and it will not be autograded in any way. That said, we strongly encourage you to use a graph implementation of graph coloring to solve your scheduling problem. In particular, if you consider courses to be vertices and draw undirected and unweighted edges between vertices if they have at least one student in common, you may find the NP-complete scheduling problem can be ‘solved’ with a simple graph heuristic – graph coloring.

Grading Information — Part 2

Not graded! Test your code independently using the provided examples (or your own)!

Part 3: Exam Scheduling

In part 3, given the corrected roster information produced by part 1 and a list of timeslots for exams, your task is to produce a valid scheduling for all courses such that there are no course conflicts for any students. As with part 2, you have total freedom over how you choose to implement scheduling. If you can optimize a brute-force solution to an NP-complete problem that won’t time out the autograder, go right ahead. However you are strongly encouraged to use a graph coloring heuristic as described below.

# INPUT:
# A std::vector<std::vector<string>> (typedef V2D) containing corrected roster information for each course
# A std::vector<std::string> containing distinct timeslots for exams
# OUTPUT:
# A V2D containing a valid scheduling for all courses
#
# The scheduling format is a V2D where the first column in each row contains the timeslot 
# and the rest of the row contains the courses assigned to that timeslot
V2D schedule(V2D courses, std::vector<std::string> timeslots)

The actual schedule function itself just requires that you produce and return a valid scheduling such that no two classes which share a student will be scheduled for an exam at the same time. Often the autograder will test using timeslot input which is larger than the actual minimum number of timeslots needed. For full credit, your scheduling heuristic should retry solutions at different starting positions until a valid scheduling has been produced. To award partial credit for students struggling on repeating the heuristic, there are a few ‘approximate’ tests which allow for slightly more colors than the graph actually needs.

Example:

Corrected RosterFile:
CS101, a, b, c
CS102, a, b
CS103, c

timeslots:
11:00 AM
1:00 PM

Scheduling:
11:00 AM, CS101
1:00 PM, CS102, CS103

Here we can see that one valid (and optimal!) scheduling is giving CS101 at one timeslot and both other classes (which have edges to CS101 but not each other) can be given at the other timeslot.

Greedy Coloring Heuristic

Given a graph (G = V, E), a graph coloring is an assignment of labels to the vertices according to a context-dependent constraint. To solve the scheduling problem, the simplest constraint is simply that no two adjacent vertices are allowed to be the same color. In this way, if edges indicate a student simultaneously enrolled in two courses (as vertices) then they would need to have different colors (exam timeslots). Observe that it is easy to determine the correctness of any particular labeling however finding the smallest number of ‘colors’ that will fully label a graph requires a brute-force search in polynomial time (O(n^k)). In other words, this is an NP-complete problem!

Rather than brute-forcing the optimal solution, we will instead will rely on a greedy heuristic – an algorithm which is not guaranteed to find the optimal solution but will get us a valid solution quickly.

The graph coloring heuristic we are using is very simple – when at an unlabeled vertex, check all adjacent vertices for colors and pick the first color which does not belong to any neighbor. (When the neighbor vertex does not yet have a color, we can ignore it). This approach will not guarantee an optimal (or even very good) coloring scheme. You can see this for yourself by taking different ‘visit’ paths through a small graph and observing the color output.

For example, if we ‘visit’ vertices in alphabetical order (A, B, C, D, E) then the heuristic will produce the following labeling (we often represent colors by numbers for convenience):

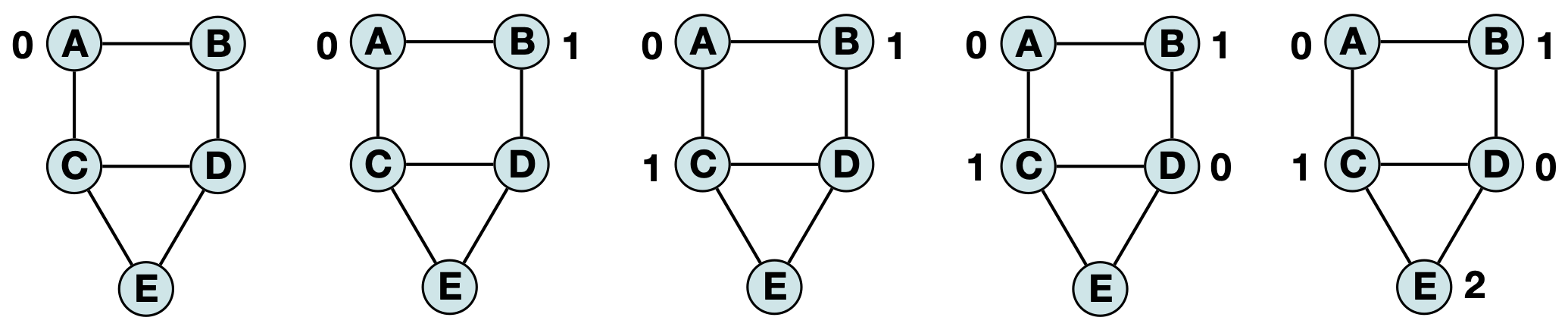
However, if we ‘visit’ vertices in based on the highest degree to lowest degree (C, D, A, B, E) we get a similar (but distinct) labeling:

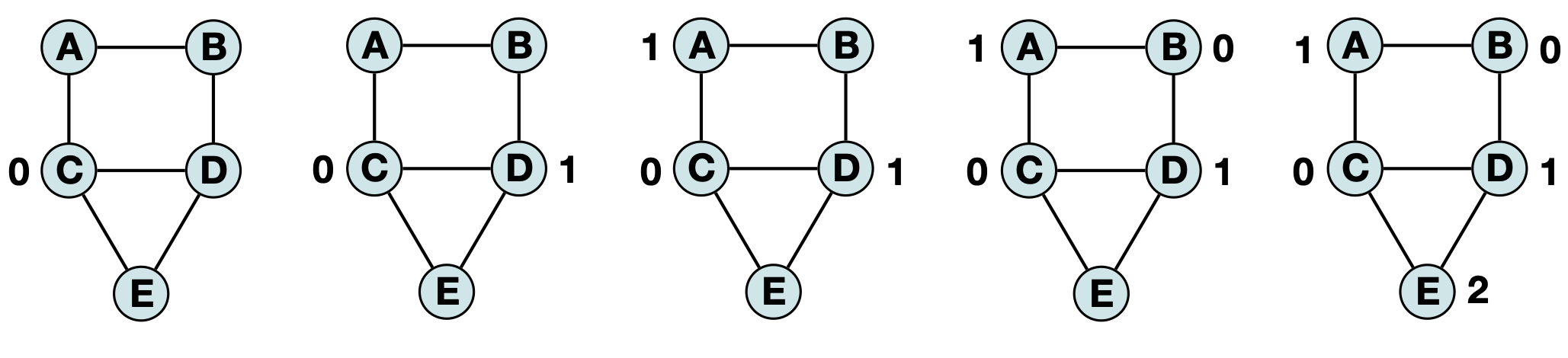
You can decide for yourself what order works best – there will be many possible colorings which use the same total amount of colors. Accordingly, the autograder will grade based on the correctness of your labeling, as long as it does not time out the autograder or use more colors (timeslots) than the provided vector has. The one notable exception is that sometimes there is no valid labeling – your code should be able to self-terminate after trying every vertex as a potential start node. Note: This is a greatly reduced subset of the full brute force search, which would require every possible start node (and every possible combination of second node, third node, etc…). If your implementation does not find a valid labeling in O(|V|), you can assume a valid labeling is impossible and return a V2D containing a single row with value -1.

Grading Information — Part 3

The following files are used to grade mp_schedule:

• src/schedule.cpp
• src/schedule.h