Week Five Lecture Notes

Nested quantifiers

Which of the following statements are true?

1. $\forall x \in \mathbb{R}, \ \exists y \in \mathbb{R}, y^3 \le x$
2. $\exists y \in \mathbb{R}, \ \forall x \in \mathbb{R}, y^3 \le x$
3. $\exists x \in \mathbb{N}, \ \forall y \in \mathbb{N}, \text{GCD}(x,y) = 1$
4. $\forall x \in \mathbb{Z}, \ \exists y \in \mathbb{Z}, x = y^2$

Answers:

1. TRUE. For any choice of $x$ there is a smaller real value $z$. Take the cube root of $z$ to get $y$.
2. FALSE. For any choice of $y$ there is some smaller $x$.
3. TRUE. $x=1$ will give $\text{GCD}(x,y) = 1$ for all $y$.
4. FALSE. Take $x=2$ as a counterexample. There is no integer $y$ that when squared equals 2.

Onto proof

Let \(f: \mathbb{Z}^2 \rightarrow \mathbb{Z}\) such that \(f(x,y) = 4x + 3y\)
Claim: f is onto

A function \(f:A\rightarrow B\) is onto if and only if

For every k in B, there is a value j in A such that f(j) = k.

So our specific function f is onto if and only if

For every integer k, there is a pair of integers \((x,y)\) such that f(x,y) = 4x + 3y = k.

On scratch paper

How to get 7 as output? input (1,1)

How to get 1 as output? input (1,-1) or (-2,3) or ....

How to get k as output? input (k, -k) or (-2k, 3k) or ...

For the proof, pick one way to find the pre-image of an output value k. Let's use (-2k, 3k).

Proof:

Let \(k \in \mathbb{Z}\).

Consider \((-2k,4k) \in \mathbb{Z}^2\).

\(f(-2k,3k) = 4(-2k) + 3(3k) = -8k + 9k = k\). So \((-2k,3k)\) is a pre-image of k.

Since k was arbitrarily chosen, this means that every integer k has a pre-image. So f is onto.

One-to-one proof

Let \(g:\mathbb{Z} \rightarrow \mathbb{Z}\) be one-to-one.
Let \(f:\mathbb{Z} \rightarrow \mathbb{Z}^2\) such that \(f(x) = (g(x)|x|, |x|)\).
Prove that f is one-to-one.

A function \(f: A \rightarrow B\) is one-to-one if

1. For any x,y in A, if \(x \not= y\), then \(f(x) \not= f(y)\) or
2. For any x,y in A, if \(f(x) = f(y)\), then \(x = y\).

Proofs normally use the second form.

Slightly buggy proof:

Let \(x\) and \(y\) be integers. Suppose that \(f(x) = f(y)\).

By the definition of \(f\), this means that \((g(x)|x|,|x|) = (g(y)|y|,|y|)\).

So \(g(x)|x| = g(y)|y|\) and \(|x| = |y|\).

So \(g(x)|x| = g(y)|x|\).

Dividing the this equation by \(|x|\), we get \(g(x) = g(y)\).

Since g is one-to-one, this implies that x = y, which is what we needed to prove.

Ooops: what happens if \(x=y=0\)?

Correct proof

Let \(x\) and \(y\) be integers. Suppose that \(f(x) = f(y)\).

By the definition of \(f\), this means that \((g(x)|x|,|x|) = (g(y)|y|,|y|)\).

So \(g(x)|x| = g(y)|y|\) and \(|x| = |y|\).

There are two cases:

Case 1: \(|x| = 0\). So \(x = 0\). Since \(|x| = |y|\), \(y\) must also be zero. So \(x= y\).

Case 2: \(|x| \not = 0\). Since \(g(x)|x| = g(y)|y|\) and \(|x| = |y|\), we have \(g(x)|x| = g(y)|x|\).

Dividing this equation by \(|x|\), we get \(g(x) = g(y)\). Since g is onto, this implies that \(x = y\).

In both cases, \(x=y\), which is what we needed to prove.

Obstruse abstract proof with both onto and one-to-one

Claim: For any sets A, B, and C, and any functions \(g: A\rightarrow B\) and \(f: B\rightarrow C\), if \(f \circ g\) is one-to-one and g is onto, then f is one-to-one

What does this even mean and why do I think it's true?

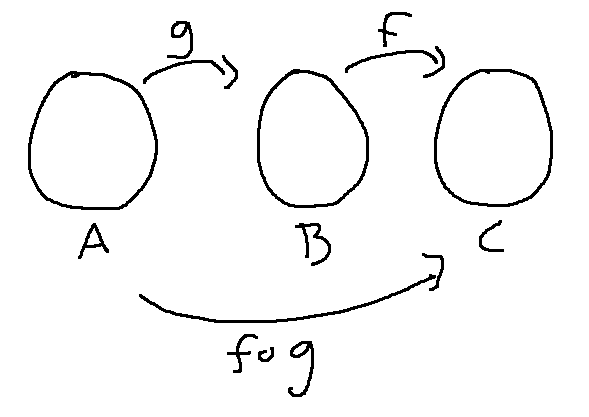
Recall: \((f \circ g)(x) = f(g(x)) \)

Bubble diagram for keeping track of what's going on:

Why does g need to be onto?

Long ago, ten CS theory faculty played World of Warcraft and each one had an avatar. Jeff Erickson's avatar \(e_J\) might have been an elf with a purple braid. We can model this with two functions:

g:{CS theory faculty} \(\rightarrow\) {World of Warcraft avatars}
f: {World of Warcraft avatars} \(\rightarrow\) {hairstyles}

Let's say each theory faculty member had an avatar with a different hairstyle. Then \(f \circ g\) would be one-to-one.

But there were about 10 million World of Warcraft subscribers and only about 3000 hairstyles. So some avatars must have shared hairstyles. So f can't be one-to-one.

Here's the picture if Michelle Obama was also playing as an elf (\(e_M\)) with the same purple braid as Jeff's avatar.

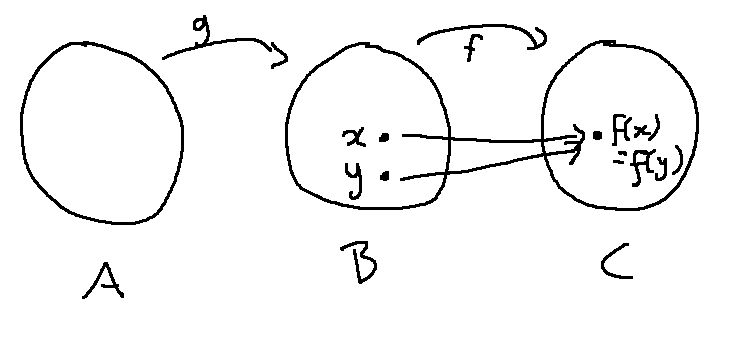
So our claim won't work unless g's outputs cover all of B.

Proof by picture

Pick \(x\) and \(y\) from B. Suppose \(f(x) = f(y)\). We need to show that \(x=y\).

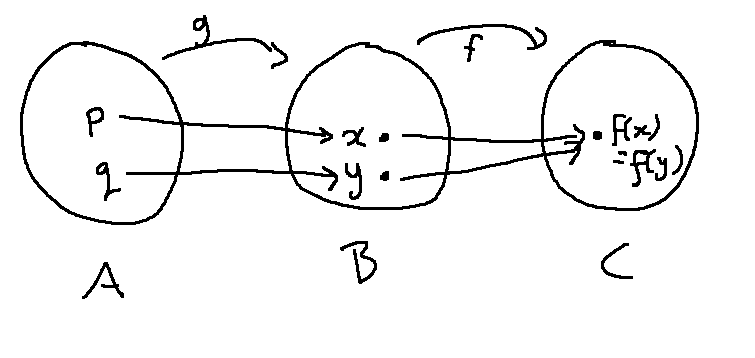
\(g\) is onto. So we have pre-images for \(x\) and \(y\). \(g(p) = x\) and \(g(q) = y\).

Since \(f \circ g\) is one-to-one:

\((f \circ g)(p) = f(g(p)) = f(x)\)
\((f \circ g)(q) = f(g(q)) = f(y)\)

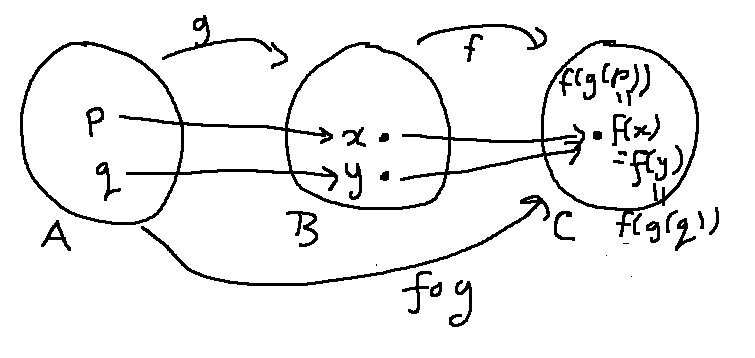
Since we know \(f(x)= f(y)\), we have \((f \circ g)(p) = (f \circ g)(q)\).

Since \((f \circ g)\) is one-to-one, this means \(p=q\) and therefore \(x=y\).

Formal proof

Proof:

Let \(A\), \(B\), and \(C\) be sets and suppose that \(g: A\rightarrow B\) and \(f: B\rightarrow C\) are functions. Also suppose that \(f \circ g\) is one-to-one and g is onto.

Let \(x\) and \(y\) be elements of \(B\). Suppose that \(f(x) = f(y)\). We need to show that \(x = y\).

Since \(g\) is onto, there are \(p\) and \(q\) in \(A\) such that \(g(p) = x\) and \(g(q) = y\).

\((f \circ g)(p) = f(g(p)) = f(x) = f(y) = f(g(q)) = (f \circ g)(q)\)

So \((f \circ g)(p) = (f \circ g)(q)\). Since \(f \circ g\) is one-to-one, this means that \(p=q\).

Since \(p=q\), \(g(p) = g(q)\). So \(x = g(p) = g(q) = y\). So \(x = y\).

We've shown that \(f(x) = f(y)\) implies that x=y. So f is one-to-one. \(\Box\)