Conway's Game of Life

So far, we've seen state diagrams with a finite number of states. But some of the most interesting applications involve infinite state spaces. A good example is John Conway's Game of Life. It's actually a little simulator, very loosely motivated by the behavior of populations. The player gets to input the starting state and then the rules take over.

The playing space is an infinite checkerboard. You start by marking soem cells as "live". When moving from step to step, you consider the eight neighbors of each cell (i.e. diagonal neighbors count).

• A cell with 0-1 live neighbors, or 4-8 live neighbors, stays/becomes dead.
• A cell with 2 live neighbors keeps its current status.
• A cell with 3 live neighbors stays/becomes live.

Here's a simulator that we can play with:

• simulator by Edwin Martin (edwin@bitstorm.org)

This starting configuration dies away:

  XXX
  X X
  

This one doesn't change:

    XX
   X  X
    XX   
  

This one turns into an oscillator:

    X
   XXX
    X   
  

Gliders

When the game was published in Scientific American in 1970, there was a big interest in working out patterns that would do fun things. For example, the "glider" (below) moves across the board. A lot of this had to be worked out on graph paper, because there were very few computers and they were very primitive.

glider

    X X
     XX
     X   
  

You can argue about whether a glider needs an infinite state space. Perhaps we can simply re-normalize the playing field so that it follows the glider. However, if your starting configuration contains a non-moving object as well as the glider, then the state space is clearly infinite because the distance between the two objects increases without bound.

Even more interesting is a glider gun, first produced by Bill Gosper. This generates an increasing sequence of gliders, so that the number of live cells in the system increases.

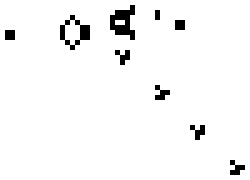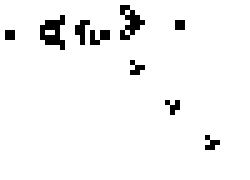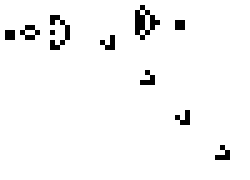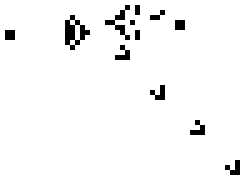
glider gun from wikipedia

Wrap up

Notice that a Game of Life configuration does one of three things:

• "Halts": It stops changing after a while.
• "Repeats": It gets into a repeating loop after a while.
• "Aperiodic": The configuration keeps changing but it's not returning to the same configuration.

If we just had the first two types of behavior, we could watch the system for a while and it would eventually halt or repeat a state. However, it's not clear how to tell whether the system is aperiodic or we just haven't waited long enough to see a halt or repeated state.

Closely related to the aperiodic behavior is the fact that you can simulate a Turing Machine, i.e. a very simple stripped-down computer, using the Game of Life.