Learning Objectives: This Lab is not to be worked in groups. Each student must work this Lab. By completing this Lab exercise you should be competent in the following learning objectives:
Simple use of the GNOME Desktop.
How to enter/exit the Matlab environment.
Use Matlab arithmetic operators on scalars, row vectors, and column vectors.
Use Matlab's built-in editor.
Use of Matlab Help facility.
Symbolics using Matlab
View the course website using Mozilla Firefox.
Lock your screen to protect your work
Instructions:
Read the instructions below carefully. Each student should perform the following on an individual basis. However, you should be able to get assistance from any student in your lab. If you can't solve it, ask the TA.
Passing of the Lab will require that you answer all the questions on the lab answer sheet and submit your answers thru Compass GradeBook. Ask your lab TA how you can submit your answers.
Log onto an EWS account and follow the instructions for Part 2 thru Part 9.
Using your mouse, left click the Applications menu (located at the top of the screen) then choose EWS Software and finally Matlab.
Wait for the Matlab prompt ">>" to appear and then type the
following commands:
(When entering commands, don't include the ">>" symbol.)
Matlab works like a high powered hand calculator. Type the
following commands at the Matlab prompt:
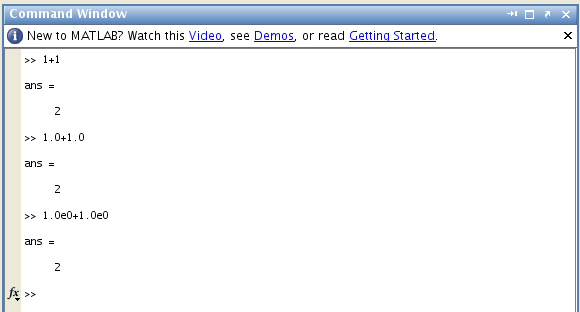
>> 1+1
>> 1.0 + 1.0
>> 1.0e0 + 1.0e0
You should see,

Therefore , Matlab doesn't distinguish between the integer 1 and the decimal representation 1.0 and scientific notation 1.0e0 . The numbers 1 or 1.0 or 1.0e0 are called scalars in Matlab ( so 2, 2.0 and 2.0e0 are the same scalar too and 101.101 and 1.01101e2 are also the same Matlab scalars).
On the answer sheet fill in the blanks with the correct answers
for questions 1 - 5.
If the answer gives a Matlab error message, don't write down the
entire message, just fill in the blanks with the word ERROR.
Before you type the following make sure to first type
>> format short e
at the Matlab prompt.
1.
>> 4 \ 1
2.
>> 1 / 4
3.
>> 2^5
4.
>> 2.0e1 - 3.0e1 * 5.0e1
5.
>> (2.0e1 - 3.0e1) * 5.0e1
Constants in Matlab are literal 1, 1.0 , 1.0e0 or symbolic , like "pi" . At the Matlab prompt type:
>> pi
Note that your answer is incorrect since the decimal expansion for
pi is infinite. This is an important point concerning
Matlab---Matlab does not implement inifinite precision arithmetic.
The difference between Matlab's value and the correct value of pi
is called round-off error
( http://mathworld.wolfram.com/RoundoffError.html ) . However we
are not "seeing" the full precision of Matlab. Use the format
command to see all the digits of Matlab's internal representation
of pi .
>> format long e
>>pi
Using Help
If you want to know the details of any Matlab command xxx (or
function yyy) type doc xxx (or doc yyy), so type,
>> doc format
or you can select/highlight whatever command you need help with and press the F1 function key at the top of the keyboard. To close the pop-up, just press Esc key when the pop-up is selected.
You can also get to Matlab Help by using the Matlab Help facility.
For example, on the Matlab Menu Bar, click Help. Next click on
"Product Help" in the drop-down list. Finally, type "format" in
the search box and press the Enter key on your keyboard).
Matlab has other constants, such as i (imaginary , in Matlab you
can also use j instead of i) , Inf (infinity) , and NaN (which
means Not a number )
On the answer sheet answer questions 6-20.
6.
>> Inf + 1
7.
>> Inf - 1
8.
>> 1 / Inf
9.
>> Inf * Inf
10.
>> 0 * Inf
11.
>> (-1) * Inf
12.
>> Inf - Inf
13.
>> 1 / 0
14.
>> -1 / 0
15.
>> i * i
16.
>> format short
>> 1 + 2*i
17.
>> 1 + 2i
18.
>> (1 + 2i) - (3 + 4i)
19.
>> (1 + 2i) * (3 + 4i)
20.
>> (1 + 2i) / (3 + 4i)
To make a list in Matlab use a pair of square brackets [ ] . For
example at the Matlab command prompt type,
>> [ ]
Ok that's the empty list,
>> [ 1 2 3 4 ]
>> [ 1 2 3 4 [ 5 6 7 8] ]
You can optionally use the comma as a separator rather than a
space (blank).
>> [1, 2, 3 ,4]
>> [ [1, 2, 3, 4] , [5, 6, 7, 8] ]
or
>> [ 1 2, 3 , 4]
The lists above are examples of row vectors (row lists). In Matlab
you can also make column lists using the semi-colon.
>> [1 ; 2 ; 3 ; 4]
You can change a row vector into a column vector and vice versa
using the apostrophe operator.
>> [ 1 2 3 4]'
>> [ 1 ; 2 ; 3 ; 4]'
In the future we will dicuss how you can create tables of values
(called matrices) in Matlab. We will also apply
commas/blanks and semi-colons to tables.
The general rule for comma/blank (example [xxx , yyy]) and
semi-colon [xxx ; yyy ] in Matlab is the following:
the comma or blank means paste the value yyy to the right of xxx
whereas a semicolon means paste the value yyy below xxx.
However, the new vector (or table) must be a full rectangle
otherwise Matlab will generate an error. For example type,
>> [ 1 2 3 4 ; 5]
Okay it's the future, so lets do a table,
>> [ 1 2 3 ; 4 5 6]
Important: The length of a vector the number of
values it holds. The size of a list (vector) or table
(matrix) is the number of rows by number of columns.
You can add two vectors if and only if they are of the same size,
that is they have the same number of rows and the same number of
columns. For example,
>> [ 1 2 3] + [ 4 5 6]
but not,
>> [ 1 2 3] + [ 4 5]
The Matlab colon operator is useful in creating lists,
>> 1 : 4
>> .5 : 2.5
So a : b means create a list by starting at a and keep adding 1
until you get to b. But what if b is not an integer multiple of a?
You will stop before you exceed b.
>> 1 : 2.5
1 is the default stepsize for the colon operator, but you can
choose your own, for example for a step size of 2 type,
>> 1 : 2 : 7
You can also choose a negative stepsize,
>> 7 : -2 : 1
On the answer sheet answer questions 21-26.
21.
>> [ 1 2 3]'
22.
>> [1; 2; 3] - [4; 5; 6]
23.
>> [1; 2; 3] + [1 2 3]
24.
>> [ [1 2 3] ; [1 2 3] ]
25.
>> x = -1 : 3
26.
>> x = 1 : 3 : 11
Matlab variables are likened to drawers in your desk. They(the
drawers) have a loction and hold stuff. To create a variable, use
an assignment statement like,
>> x = [ 1 2 3]
Now to dump the stuff out of your drawer just type,
>> x
Its not the same as emptying your drawer since the the stuff is
still there, type again,
>> x
Important: An assignemnt statement works this way, evaluate
what's on the right hand side of the equals and then assign the
results of the evaluation to the variable on the left hand side of
the equals sign. For example type,
>> [ 1 2 3] = x
which doesn't work since the varible must be on the left hand side
of the equals.
Evaluation of the right hand side means use the current values of
the variables, for instance, if x was assigned [ 1 2 3] then
typing,
>> y = x + [ 1 2 3]
means , evaluate [ 1 2 3] + [ 1 2 3] ( which is [ 2 4 6] ) and
then assign [ 2 4 6] to the variable y.
As a note, when you type,
>> [ 1 2 3]
since you haven't used an assignment statement (=) Matlab
evaluates the expression and assigns the results to the variable ans
.
ans =
1 2 3
You can treat ans as any other variable,
>> ans
1 2 3
On the answer sheet answer questions 27-29.
27.
>> x = [0 2 1];
>> y = x + [2 4 2]
28.
>> x
29.
>> y = [x, 2 3 4]
A Matlab function is a sequence of Matlab statements (the code) . These Matlab statements are evaluated sequentially, using the input values (if any) provided in the call to the function. The function then may return a value or values. Functions differ from scripts in that all function variables are local to the function. That is, the variables in a function can't been seen or modified in the Matlab command window.
The basic Math functions you find on your hand calculator are
included in Matlab for example,
>> sin( pi/2) (formally when we type this and hit the Enter
key in programming terminology we say we "call" the sin function)
>> exp (1) ( e1)
>> log( exp(1)) (natural log, that is, log base e, standard
math notation is ln)
>> log10(10) ( log base 10)
>> abs(-1) ( absolute value)
>> sqrt( 4) (square root)
If you forget or want to get more details as to what these
functions do, you can use Matlab Help or type help xxx at the
Matlab command window.
Matlab has innumerably many functions. Consider a few we will use
later this semester.
On the answer sheet answer questions 30-42 .
30.
>> x = linspace(-2, 2, 5)
31.
>> x = linspace(0, 10, 100);
(don't forget this semi-colon, it means suppress out to screen)
>> min(x)
32.
>> max(x)
33.
>> x = [2 3 5];
>> sum(x)
34.
>> sum([1; 4; 5])
35.
>> z = [1
2 2 2];
>> cumsum(z)
36.
>> x = [1 3 6 12];
>> diff(x)
37.
>> x = [3 5 10];
>> mean(x)
38.
>> x = [3 5 10];
>> median(x)
39.
>> x = [1 2 3 4];
>> median(x)
40.
>> x = [1 2 3 4];
>> diff(cumsum(x))
41.
>> sqrt(-1)
42.
>> abs(3 - 4i)
All Matlab programs are either scripts or functions. In this part
of Lab 1 we will write a script. In Lab 2 we will write a function
and compare the differences between functions and scripts.
A MATLAB script file contains any Matlab command you can enter at
the Matlab prompt.
To write a script you first open the Matlab editor using the
"edit" command. Then after your type in your code (Matlab
statements) you save your file. Script files can have any name you
choose but their file extension must be ".m". To execute a script
file, while in the Matlab environment, type in the name of the
script file.
All the commands (but not comments ) in a script file are executed. The execution starts with the first command at the top of the file and proceeds sequentially downward. A comment is anything (text, numbers, ...) that follows (on the same line) the "%" symbol. Comments are informative messages programmers include to help remind themselves and explain to others what the code is trying to accomplish.
You may choose to comment a script file. A comment is not executable but gives information for the programmer.
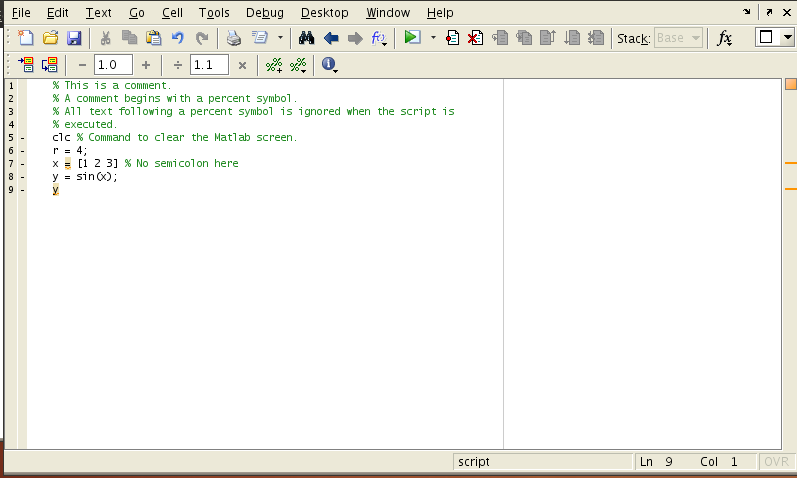
Open the Matlab editor by typing (use your last name not "lastname")
>> edit lastname.m
If you are asked whether to create the file, choose yes.
in the Matlab command window. Type the following Matlab commands into ".m" and click File then select Save or Save AS from the menu.
% This is a comment. % A comment begins with a percent symbol. % All text following a percent symbol is ignored when the script is % executed. clc % Command to clear the Matlab screen. r = 4; x = [1 2 3] % No semicolon here y = sin(x); y

On the answer sheet answer questions 43-50 .
43. Before we run the script file, in the Matlab environment, enter the who command, which lists all your variables:
>> who
List the variables: (Write "No variables" if no variables appear)
44. Now type the following,
>> clear >> who
List the variables:______________________________
45. Next type,
>> r = 1; >> who
List the variables: ______________________________
46. Type the following,
>> r
What is the value of r? _________
Use the "what" system command to make sure that you have correctly saved your lastname.m file.
>> what (this lists the .m and .mat files in your directory)
If you don't see the "lastname" file ask your TA for help before you proceed.
47. Run the script by typing your last name at the Matlab prompt.
Write what is displayed on your screen:_______________________________
48. Type
>>r
What is the value of r? _________
49. So, can running a script alter the value of a workspace variable? Y / N
50. Again, type
>> who
List the variables in your workspace:
Like Mathematica, Matlab can be used to perform symbolic
differentiation, integration and to compute limits. Symbolic
operations like differentiation, integration or limits require
that we tell Matlab which symbolic variables are in use in our
formula. To do this we need to use the syms command (not
to be confused with "The Sims").
Example 1: Find the indefinite integral of x2 with
respect to x
>> syms x ( we tell Matlab that x is a symbolic variable not
a variable in the sense discussed above in Part 4)
>> int(x*x,x) ( the first argument in the call to the int
function is x*x and the second argument is x)
When there is no ambiguity, you can omit the argument that lists
the symbolic variable. Type,
>> int(x*x)
The result is symbolic so you can use the result is the input to
another function. For example, type,
>> result = int(x^2,x)
Let's check our answer by differentiating with respect to x
>> diff(result,x,1) ( 1 means first derivative) Note
that we used the diff function in question 36 but its input wasn't
a symbolic variable so diff has
works in a different way when the input is specific numerical
values.
Also note that since there is only one symbolic variable in the
input "result" there is no ambiguity about what variable we are
differentiating with respect to so we can write,
>> diff(result)
Example 2: find the limit of x2/x as x goes to 0
>> limit(x^2/x, x, 0)
Example 3: The formula may contain non-symbolic variables as in,
>> a = 2.5
>> solution = int(a*x,x)
On the answer sheet answer questions 51-53 .
51. Compute the derivative of t3 with respect to t,
>> syms t
Note: When you execute the syms
command, you may see a page of red text. If you do, please restart
Matlab.
Fill in the blank with Matlab code to call the diff function to compute the second derivative of t3. You must use the diff function.
>> solution =
_______________________________ (The solution should be
6t,
but you should write the command used to find the
solution.)
Did you notice that in question 26 the same diff function works
with vector inputs and does NOT compute the derivative. Here diff
detects that it is passed a symbolic expression so that it
computes the symbolic derivative.
52. Write the result of executing the following code,
>> syms y
>> limit(sin(y) / y, y, 0)
53. Write the result of executing the following code,
>> syms z
>> diff(int(z^4, z), z)
You can Exit matlab now by typing
>> exit
at the Matlab prompt ">>" .
On the answer sheet answer questions 54 - 55.
54. Find in the course syllabus: Find the grade range(in points) for a B+ grade for CS101:
55. Click the "Staff " hyper-link: What is the email address of your lab TA?
For your reference, the course website is at:
http://courses.engr.illinois.edu/cs101/su2015
Although some lab work is done in groups, the MPs(machine problems) must be worked individually. It is the students responsibility to make sure that his/her code is not copied since this would constitute cheating--- see Lecture 0 of the class notes. When you are working on your MP and have to leave the lab for a brief time, you should choose Lock Screen from the System menu at the top of the screen. When you come back into the lab, click on the computer screen and type your password to unlock the terminal.
To complete the first Lab activity you should Lock Screen and then unlock the screen again. Once you have done that, minimize all the windows on the screen so the desktop is showing.
56. Create a screenshot of your computer screen. Do this by choosing Applications->Accessories->Take Screenshot from the main Linux menu. Choose "save to clipboard" option. Then paste your solution into the lab1_answers.odt file.
Submit the lab 1 answer sheet on Compass.
Log out: Choose "Log Out" from the System menu. NEVER leave your
computer without logging out since someone else entering the lab
after you would have access to all your files.
Congratulations you have just finished Lab #1 !!!