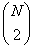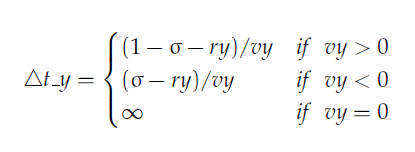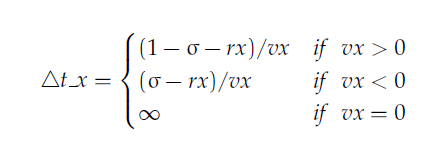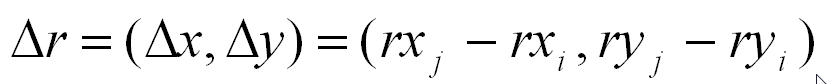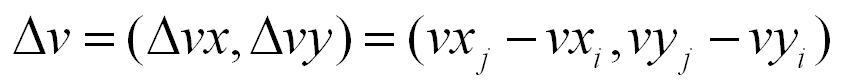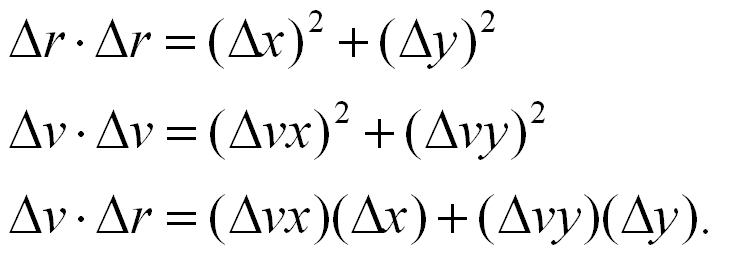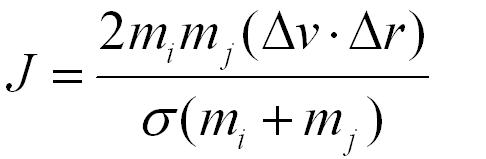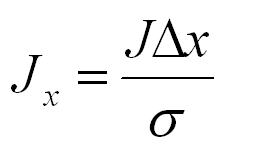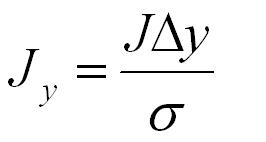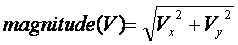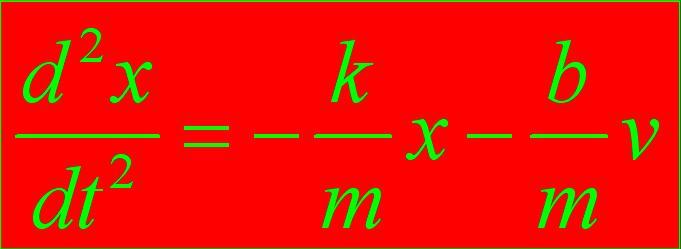You will need to read the following instructions in sections 1) thru 3). You will begin coding in section 4) Implementation

1) Introduction

1.1) Dynamics of Hard Spheres - Your Honor’s Project

The motion of molecules in a gas, the dynamics of chemical reactions, atomic diffusion, sphere packing, the stability of the rings around Saturn, the phase transitions of cerium and cesium, one-dimensional self-gravitating systems, a game of billiards or snooker, front propagation are all examples of dynamics. Also, they have the additional similarity of having spherical or nearly spherical colliding objects in each of the above presented examples. We can take some time here to observe three facts: 1) Their inter-disciplinary nature, 2) The role of Computer Programming and 3) The fact that a common program written to simulate the motion of colliding particles can describe all these phenomena. We could also observe the fact that all these are at least related to the Brownian Motion which was introduced earlier.

The purpose of this programming assignment is to develop a computer program which could represent to an acceptable level of accuracy, the above mentioned condition; that is, to simulate the motion of “N” colliding particles based on the laws governing elastic collisions and basic dynamics.

[P.S.: We are really grateful to the Computer Sciences Department of the Princeton University for providing us with useful material in this respect. More information regarding this can be found here.]

2) Modeling

2.1) In General

Modeling refers to the process of the reproduction of the given problem, usually to a smaller scale. Modeling often involves certain simplifying assumptions which make the process of creating a model simpler.

The modeling involved in dynamical analysis is in turn sub divided into 2 major steps:-

a) Creating an Analytical Model

b) Obtaining a Mathematical Model from the Analytical Model.

The process of obtaining the Analytical Model consists of the following main steps:

a) A list of simplifying assumptions which permit to reduce the real life problem into a simpler analytical model.

b) Drawings that depict the Analytical Model.

c) A list of design parameters.

To create a useful Analytical Model, you must clearly have in mind the intended use of the analytical model, that is, the types of behavior of the real system that the model is supposed to represent faithfully.

Once the analytical model of the structure has been created, we can apply the concerned physical laws to convert the dynamical equations of the system under question into Mathematical equations. These Mathematical equations so obtained are termed the “Mathematical Model”.

In practice, you will find that the entire process of creating first an analytical model and then a mathematical model may be referred to simply as mathematical modeling.

2.2) Analytical Modeling of the “Molecular Dynamics” Problem

Any real life problem is a complex one. However, it is observed that certain simplifying assumptions can be made which reduce the complexity of the problem without a great deal of reduction in the accuracy of the desired variables. In other words, these assumptions make life much simpler than what it would be otherwise.

For this problem, one major simplification has been made. The molecule (or the sphere) under study is an elastic body, which should undergo elastic deformations upon collisions. However, it has been observed that neglecting these small deformations does not affect the end result very much, although it reduces the complexity of the problem a good deal. So, in the analytical model of this problem, we assume that atoms or molecules or the spheres (these three terms are equivalent; the use of any of these three words in future would represent the same.) in the container behave as “hard spheres”, also called the “billiard ball model”. When we focus on the two-dimensional version of this, they behave as the “hard disc model”.

We will do our calculations in 2D. (3D would not be much more difficult but we will leave that for you to do for fun.)

In addition to this major assumption, we also make other simplifications which result in the following salient features of this model:

a) “N” particles in motion.

b) All particles are confined in the ‘unit box’.

A box of unit height and width, 0 <= x <=1, 0 <= y <= 1.

c) Particle ‘i’ has the position (rx_i, ry_i), velocity (vx_i, vy_i), mass m_i, and radius σ_i.

d) All particles interact via elastic collisions with each other and with the reflecting boundary.

e) No other forces are exerted. (e.g. no gravitaional effect on particles or between particles.) Thus, particles travel in straight lines at constant speed between collisions.

There are two natural approaches to simulating the system of particles.

A) Time-driven simulation:

Discretize time into quanta of size dt. Update the position of each particle after every dt units of time and check for overlaps. If there is an overlap, roll back the clock to the time of the collision, update the velocities of the colliding particles, and continue the simulation. This approach is simple, but it suffers from two significant drawbacks.

First, we must perform on the order of N² collision checks per time quantum ,

(actually N choose 2 particle-to-particle collisions, 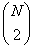= N*(N-1)/2 plus 2*N checks for the particle-wall collisions).

Second, we may miss collisions if dt is too large and colliding particles fail to overlap when we are looking. To ensure a reasonably accurate simulation, we must choose dt to be very small, and this slows down the simulation.
We will NOT do time-driven simulation in this MP.

B) Event-driven simulation:

With event-driven simulation we focus on those times at which interesting events occur. In the hard disc model, all particles travel in straight line trajectories at constant speeds between collisions. Thus, our main challenge is to determine the ordered sequence of particle collisions. We address this challenge by maintaining a event matrix of future events for each particle. At any given time, the event matrix contains the next future collision that would occur for each particle, assuming each particle moves in a straight line trajectory forever. As particles collide and change direction, some of the events scheduled on the priority queue become "stale" or "invalidated", and no longer correspond to physical collisions. Thus we will have to update this event matrix. For example, we have the following events in the queue:

particle# |  time-to-next-collision | particle/wall

1   .02     5  ( particle #1 will collide in .02 seconds with particle #5)

2   .2       1   ( particle #2 will collide in .2 seconds with particle #1, we haven't yet taken into account here that particle #1 will first collide with paricle #5 )

3   .05    -1 ( partice #3 will collide with  the horizontal wall  in .05 seconds,  -1 means horizontal wall collision)

4   .4      -2 ( particle #4 will collide with the vertical wall in .4 seconds, -2 means vertical wall collision)

5   .02     1  ( particle #5 will collide in .02 seconds with particle #1)

…

N   Inf     -3   ( particle #N will not make any collisions since a value of -3 means zero velocity so no collison with any wall,  and there is also no particle collisions. Inf is the Matlab constant for +infinity.)

From the values shown above the next collision for any of the particles is between Particle 1 and 5 since the time for this collision is the smallest value ( .02 seconds).
Particle 2’s next collision is with Particle 1 but that won’t happen since Particle 1 will collide with Particle 5 first ( in .02 seconds).

The event matrix will have N rows but just two columns (since the first column above is always 1 thru N we don’t need to store this in the event matrix.).

So the format of the event matrix will be such that the i-th row of the event matrix has the form:

[ time-to-next-collision   j   ]

where j is an integer from 1 to N  representing a particle number or -1,-2 representing a horizontal or vertical wall collision respectively or -3 meaning NO COLLISION with wall or partice.

In the case where j = -3 instead of using the Matlab Inf as in a row value of

[ Inf   -3]
instead we could record this row as

[ arbitrary_real_number    -3]

if we wanted to avoid using the Matlab constant Inf.

 

3) The Math

In this section we present the formulas that specify if and when a particle will collide(hit) with the boundary (wall) or with another particle, assuming all particles travel in straight-line trajectories.
For simplicity we will avoid considering simultaneous collisions with 3 or more particles or simultaneous collisions of separate pairs of particles or a particle that hits the corner of the box ( hits both walls simultaneously).

 

3.1) Collision Prediction

I) Collision between particle and a wall:

  Assume you had only a single particle of radius σ in the unit box (0 <= x <= 1 and 0 <= y <= 1) where the center of the partice is located at (rx, ry) and thus σ <= rx <= 1-σ and σ <= ry <= 1-σ , with velocity (vx, vy).
The questions we need answered are:

1) Which wall will the particle hit, if any? 
2) What is the new position vector (rx', ry') and new velocity vector (vx', vy') after the collision.
3) How much time does it take to hit the wall Δt?

Here is our strategy for answering the above questions.
We will answer 3) first then use our results to determine 1) and then 2) will follow.

To answer question 3) ,

If the inital velocity is zero i.e.  (vx, vy) = (0,0) then the particle would not move and thus not make contact with a new wall( of course it could be touching a wall and not moving too but that doesn't change the fact that the particle will not hit a new wall). This answers question 1)  and to answer question 2) since vx = vy = 0 then its new position at any future time would be (rx', ry') = (rx, ry) and new velocity (vx', vy') = (0,0).
Else if the particle were moving, ie. vx and vy are not both 0 then then there must be a future contact with the walls of the unit box. Lets solve this problem in a lazy way. We first assume that the box has no vertical walls, only horizontal walls (extended infinitly in both directions) and then try compute Δt_y the time the hit the horizontal wall. Next assume that the box has no horizontal walls jut vertical walls and then try to compute Δt_x the time to hit the vertical wall. Now that we have computed Δt_y and Δt_x find the smallest of the two Δt = min(Δt_x, Δt_y) and that will tell us which wall is actually hit. This answers question 1). Question 2) is answered by using the formula (rx', ry') = (rx, ry) +Δt * (vx,vy) and (vx', vy') = (vx, -vy) if a horizontal wall is hit and (vx', vy') = (-vx , vy) if a vertical wall is hit.  There is a very rare case where Δt_x = Δt_y when the particle hits the corner of the box. You don't have to write code for this case. If you write code then the new positon is also given by the same formula (rx', ry') = (rx, ry) +Δt * (vx,vy) but the new velocity is given by  (vx', vy') = (-vx, -vy).

Yes, it may occur that vx > 0 and vy = 0 so that computing  Δt_y = Inf in Matlab  but since  Δt_x is finite then  Δt = min( Δt_x,  Δt_y) =  Δt_x and this is correct so your code should work correctly without any changes.
Also, it may occur that vx = vy = 0 but this would give Δt = min( Δt_x, Δt_y) = min(Inf, Inf) = Inf and that is correct so again you don't need to modify your code for this special case. If you don’t like working with Inf then in these cases set Δt = 1.0e100.

All that is left to do is to find the formulas for Δt_x and Δt_y.

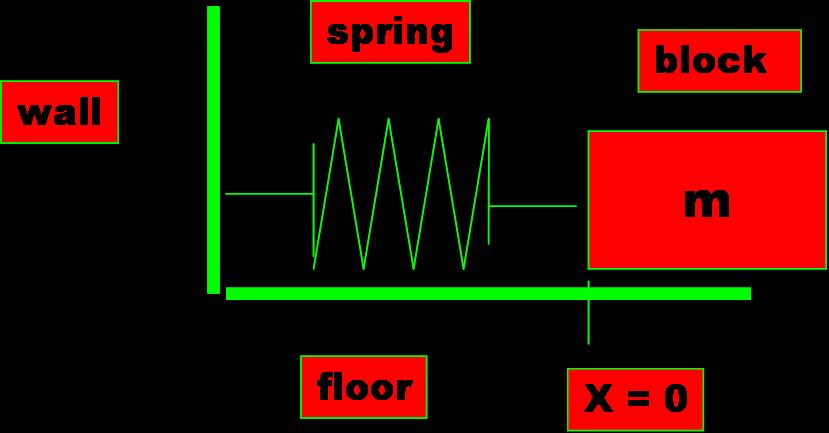
a) Δt_y  ---Horizontal Wall Collision

Given the position vector (rx, ry), velocity vector (vx, vy), and radius σ of a single particle at time t, we wish to determine if and when it will collide with a vertical or horizontal wall. the new velocity (vx', vy') =  (vx, -vy) for either upper or lower wall collision. To determine the new position  (rx', ry') consider the figure below.

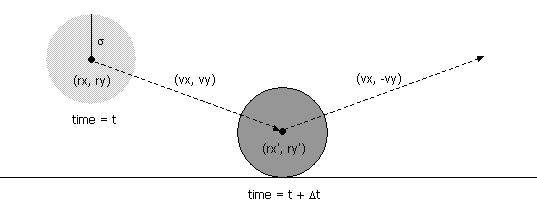
                                                                                                                                                        The figure above shows a future collision of a particle with the lower horizontal side of the boundary(wall).

A particle comes into contact with a horizontal wall at time t + Δt if the quantity ry + Δt * vy equals either σ (lower horizontal wall collision) or (1 - σ) (upper horizontal wall collison).
Solving for Δt yields:

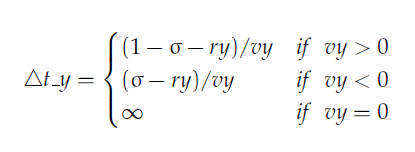
b) Δt_x ---Vertical Wall Collision

An analogous equation predicts the time of collision with a vertical wall. The

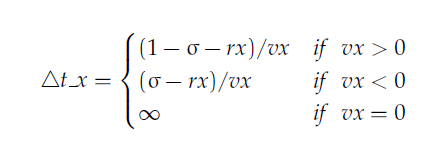
Since we are going to be dealing not with just one particle in the unit box it may occur that before a particle hits a wall of the box the particle hits (or is hit ... depending on your perspective, that is, from which particle you view the collision) another particle. We need to answer the following questions.

We are given information on particle  i   at time t , its position (rx_i , ry_i) and velocity (vx_i , vy_i )

1) Will particle i hit particle j   (whose position at time t is (rx_j , ry_j) and velocity is (vx_j , vy_j ))  ? 
2) What is the new position vector (rx', ry') and new veloctiy vector (vx', vy') at the time of collision for both particles i and j ?
3) How much time Δt does it take for particle i to hit particle j  ?

II) Collision between two particles.

Again, we will answer 3) first and if Δt  = Inf we know there is no collision but if Δt  is finite there will be a collision and then we will answer 2).

 

Given the positions and velocities of two particles i and j at time t, we wish to determine if and when they will collide with each other.

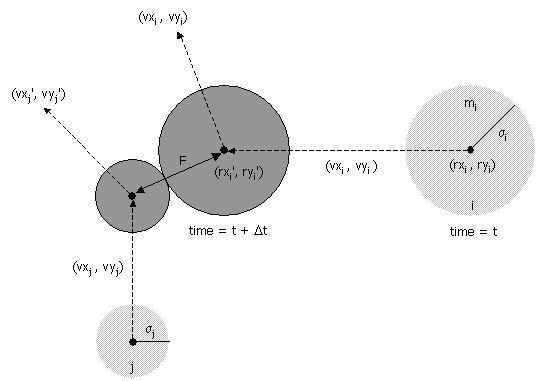
Let (rx_i' , ry_i' ) and (rx_j' , ry_j' ) denote the positions of particles i and j at the moment of contact, say t + Δt. When the particles collide, their centers are separated by a distance of σ = σ_i + σ_j. In other words:

σ² = (rx_i' - rx_j' )² + (ry_i' - ry_j' )²

During the time prior to the collision, the particles move in straight-line trajectories. Thus,

rx_i' = rx_i + Δt vx_i,   ry_i' = ry_i + Δt vy_i      EQUATION  1
rx_j' = rx_j + Δt vx_j,    ry_j' = ry_j + Δt vy_j       EQUATION  2

Substituting these four equations into the previous one, solving the resulting quadratic equation for Δt, selecting the physically relevant root, and simplifying, we obtain an expression for Δt in terms of the known positions, velocities, and radii.

      and
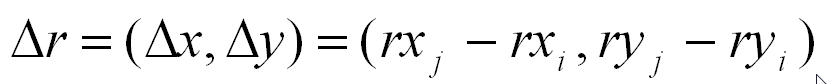EQUATION 3

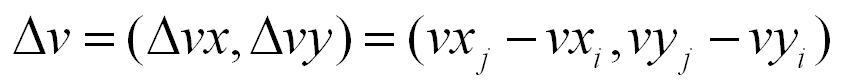EQUATION 4

     and

 

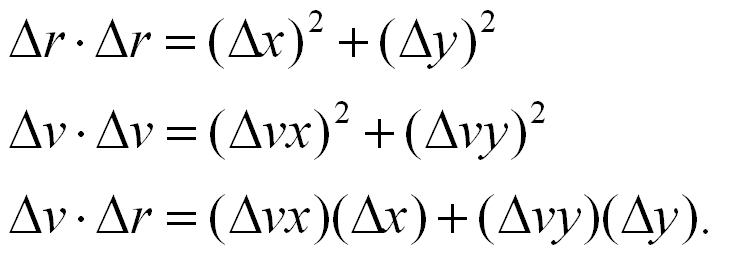
If either (Δv ⋅ Δr) ≥ 0 or d < 0, then the quadratic equation has no solution for Δt > 0; otherwise we are guaranteed that Δt ≥ 0.

 

In the event the particles i and j will collide at the future time we then need to determine the new positions and velocities. There are three equations governing the elastic collision between a pair of hard discs: (i) conservation of linear momentum, (ii) conservation of kinetic energy, and (iii) upon collision, the normal force acts perpendicular to the surface at the collision point. Students inclined towards Physics are encouraged to derive the equations from first principles; the rest of you may keep reading.

I) Collision between particle and a wall:

When two hard discs collide, the normal force acts along the line connecting their centers (assuming no friction or spin). The impulse (Jx, Jy) due to the normal force in the x and y directions of a perfectly elastic collision at the moment of contact are:

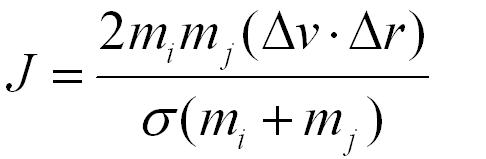
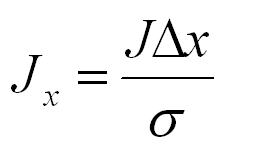EQUATION 5

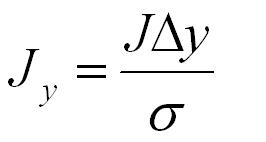EQUATION 6

 

and where m_i and m_j are the masses of particles i and j, and σ, Δx, Δy and Δ v ⋅ Δr are defined as above. Once we know the impulse, we can apply Newton's second law (in momentum form) to compute the velocities immediately after the collision.

vx_i' = vx_i + Jx / m_i, vx_j' = vx_j - Jx / m_j     EQUATION 7
vy_i' = vy_i + Jy / m_i, vy_j' = vy_j - Jy / m_j    EQUATION 8

4) Implementation

Download ALL of the following files:

main.m

start_position1.m

start_position2.m

create_event.m

update.m

box.m

plotbox.m

plotp.m

demo.p

 

Your programming in this MP will involve completing the update function.

We have given you the code for the main function but it’s a good idea to look at the code before you begin coding for the update function. There is NO checker for this MP. So you must first complete your code for the update function and then type the following at the Matlab prompt:

>> position = main(500, 1.0e-11, 'start_position1');

or

>> position = main(500, 2.0e-10, 'start_position2');

Your results should look similar to,

>> position = demo(500,2.0e-10, 'start_position2');

You can type Control-C to terminate execution.

4.1) The main function a Step - by - Step Algorithm

1. The function ‘main.m’ which has three inputs, the number of molecules N, the total time ‘total_time’ and a function that computes the initial position matrix.

2. You will be able to download two functions that compute the initial position matrix one is named start_position1.m and the other start_position2.m. The main function calls the start_position1.m or start_position2.m function that you pass to main as a function argument. Note that the start position matrix has the form:

[ x , y , vx , vy , radius , mass ] and has ‘N’ rows.

3. We first plot the position matrix.

4. Assign time = 0

5. Call the create_event function to create initial event matrix.

6. Loop while time < total_time

a. Call the update function to find the time to the next collision dt, and update both the position and event matrices.

b. Increase time by dt.

c. plot the position matrix

4.2) Event Driven Simulation … update function

When we update the event matrix we will,

1)   1) find the minimum time-to-collision value in the event matrix

2)   2) if the above event corresponds to a particle-to-particle collision then add these to the update list. The update list contains the particle number (integer) for those particles we need to update the event matrix, that is, for these particles we need to find their next collision and put that collision in the event matrix. If the next collision is particle-wall then just add this particle to the list.

3)   3) check whether there are other particles in the event list that were to collide with the particle(s) in the list above. These particles should also be added to the list.

4)   4) update the position matrix using the math below above

5)   5) reduce the time (every row in the event matrix) by the minimum time-to-collision found in 1)

6)   6) call the create_event function and update all rows in the event matrix that are in the list from steps 2) and 3)

 

 

You are required to complete the following two tasks.

First Task: Completing the code for the function “update.m”. Replace all the blanks with your code.

Second Task:  Using the start_position1  call main as shown below. The start_position1  function assigns all particles to have the same magnitude for velocity in the position matrix. Remember if the velocity of a particle is V = [Vx, Vy] then the magnitude of the velocity would be,

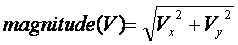
After you run the Matlab command,

>> position = main(500, 8.0e-11, 'start_position1');  % this may take 20-30 minutes and if you run it on a lab computer while and not remotely it will take less time

create a vector named velocities that contains only the magnitudes of the velocities of the particles and then display the velocities in a histogram, (see Maxwell/Boltzmann  to get an approximate view what your plot should look like. Your plot would look closer to the one shown if you increased the value 8.0e-11)

>> hist(velocities,14)

In the figure window click File/Save As and save this image as velocities.fig.

Submit the following files:
:

I) update.m

II) velocities.fig