
The first thing you need to do is to download this file: mp07.zip. It has the following content:
main.py. This file plays the game (python3 main.py).submitted.py: Your homework. Edit, and then submit to Gradescope.mp07_notebook.ipynb: This is a Jupyter notebook to help you debug. You can completely ignore it if you want, although you might find that it gives you useful instructions.grade.py: Once your homework seems to be working, you can test it by typingpython grade.py, which will run the tests intests/tests_visible.py.tests/test_visible.py: This file contains about half of the unit tests that Gradescope will run in order to grade your homework. If you can get a perfect score on these tests, then you should also get a perfect score on the additional hidden tests that Gradescope uses.grading_examples/. This directory contains the JSON answer keys on which your grade is based (the visible ones). You are strongly encouraged to read these, to see what format your code should produce.chess/,res/,tools/. These directories contain code and resources from PyChess that are necessary to run the assignment.requirements.txt: This tells you which python packages you need to have installed, in order to rungrade.py. You can install all of those packages by typingpip install -r requirements.txtorpip3 install -r requirements.txt.extracredit*: These files are for extra credit only, check the ec section for details.
This file (mp07_notebook.ipynb) will walk you through the whole MP, giving you instructions and debugging tips as you go.
Table of Contents¶
I. Getting Started¶
The main.py file will be the primary entry point for this assignment. Let’s start by running it as follows:
!python3 main.py --help
This will list the available options. You will see that both player0 and player1 can be human, or one of four types of AI: random, minimax, alphabeta, or stochastic. The default is --player0 human --player1 random, because the random player is the only one already implemented. In order to play against an "AI" that makes moves at random, type
!python3 main.py
You should see a chess board pop up. When you click on any white piece (you may need to double-click), you should see bright neon green dots centered in all of the squares to which that piece can legally move, like this:

When you click (or double-click) on one of those green dots, your piece will move there. Then the computer will move one of the black pieces, and it will be your turn again.
If you have trouble using the mouse to play, you can debug your code by watching the computer play against itself. For example,
python3 main.py --player0 random --player1 random
If you want to start from one of the stored game positions, you can load them as, for example:
python3 main.py --loadgame game1.txt
We will grade your submissions using grade.py. This file is available to you, so that you can understand how this assignment will be graded.
Let’s see what happens when we run this script:
!python3 grade.py
As you can see, all of the tests raise NotImplementedError, because we have not yet implemented the functions minimax or alphabeta in submitted.py. We will do this in the next few sections.
II. the PyChess API¶
The chess-playing interface that we're using is based on PyChess. All the components of PyChess that you need are included in the assignment5.zip file, but if you want to learn more about PyChess, you are welcome to download and install it. The standard distribution of PyChess includes a game-playing AI using the alphabeta search algorithm. You are welcome to read their implementation to get hints for how to write your own, but note that we have changed the function signature so that if you simply cut and paste their code into your own, it will not work.
You do not need to know how to play chess in order to do this assignment. You need to know that chess is a game between two players, one with white pieces, one with black pieces. White goes first. Players alternate making moves until white wins, black wins, or there is a tie. You don't need to know anything else about chess to do the assignment, though you may have more fun if you learn just a little (e.g., by playing against the computer).
Though you don't need to know anything about chess, you do need to understand a few key concepts, and a few key functions, from the PyChess API. The most important concepts are:
- player. There are two players: Player 0, and Player 1.
Player 0 plays white pieces, Player 1 black. Player 0 goes first.
- side. PyChess keeps track of whose turn it is by using a boolean called side:
side==Falseif Player 0 should play next.
- side. PyChess keeps track of whose turn it is by using a boolean called side:
- move. A move is a 3-list:
move==[fro,to,promote].frois a 2-list:fro==[from_x,from_y], wherefrom_xandfrom_yare each numbers between 1 and 8, specifying the starting x and y positions.tois also a 2-list:to==[to_x,to_y].promoteis eitherNoneor"q", whereqmeans that you are trying to promote your piece to a queen. - board. A board is a 2-tuple of lists of pieces:
board==([white_piece0, white_piece1, ...], [black_piece0, black_piece1, ...]). Each piece is a 3-list:piece=[x,y,type].xis the x position of the piece (left-to-right, 1 to 8).yis the y position of the piece (top-to-bottom, 1 to 8).typeis a letter indicating the type of piece, which can be (p=pawn,r=rook,n=knight,b=bishop,q=queen, ork=king).
To get some better understanding, let's look at the way the board is initialized at the start of the game. The function chess.lib.convertMoves starts with an initialized board, then runs forward through a series of specified moves, and gives us the resulting board. If the series of specified moves is the empty string, then chess.lib.convertMoves gives us the opening board position:
import chess.lib.utils, pprint
side, board, flags = chess.lib.convertMoves("")
print("Should we start with the White player?", side)
print("")
print("The starting board position is:")
pprint.PrettyPrinter(compact=True,width=40).pprint(board)
II.A evaluate¶
The function value=evaluate(board) returns the heuristic value of the board for the white player (thus, in the textbook's terminology, the white player is Max, the black player is Min).
For example, you can find the numerical value of a board by typing:
import chess.lib.heuristics
# Try the default board
value = chess.lib.heuristics.evaluate(board)
print("The value of the default board is",value)
# Try a board where Black is missing a rook
board2 = [ board[0], board[1][:-1] ]
value = chess.lib.heuristics.evaluate(board2)
print("If we eliminate one of black's rooks, the value is ",value)
# Try a board where White is missing a rook
board3 = [ board[0][:-1], board[1] ]
value = chess.lib.heuristics.evaluate(board3)
print("If we eliminate one of white's rooks, the value is ",value)
# Eliminate one piece from each player
board4 = [ board[0][:-1], board[1][:-1] ]
value = chess.lib.heuristics.evaluate(board4)
print("If the players are each missing a rook, the value is ",value)
II.B encode and decode¶
Lists cannot be used as keys in a dict, therefore, in order to give your moveTree to the autograder, you will need some way to encode the moves. encoded=encode(*move) converts a move into a string representing its standard chess encoding. The decode function reverses the processing of encode. For example:
from chess.lib.utils import encode, decode
# This statement evaluates to True
move1 = encode([7,2],[7,4],None)
print("The move [7,2]->[7,4] encodes as",move1)
# This statement also evaluates to True
move2=encode([5,7],[5,8],"q")
print("The move [5,7]->[5,8] with promotion to queen is encoded as",move2)
# This statement evaluates to True
move3 = decode("g7g5")
print("The move g7g5 is decoded to",move3)
II.C generateMoves, convertMoves, makeMove¶
The function generateMoves is a generator that generates all moves that are legal on the current board. The function convertMoves generates a starting board. The function makeMove implements a move, and returns the resulting board (and side and flags). For example, the following code prints all of the moves that white can legally make, starting from the beginning board:
import submitted, importlib
import chess.lib
# Create an initial board
side, board, flags = chess.lib.convertMoves("")
# Iterate over all moves that are legal from the current board position.
for move in submitted.generateMoves(board, side, flags):
newside, newboard, newflags = chess.lib.makeMove(side, board, move[0], move[1], flags, move[2])
print("This move is legal now:",move, newflags)
The flags and newflags variables specify whether or not it has become legal for black to make certain specialized types of moves. For more information, see chess/docs.txt.
II.D random¶
In order to help you understand the API, the file submitted.py contains a function from which you can copy any useful code. The function moveList, moveTree, value = random(side, board, flags, chooser) takes the same input as the functions you will write, and generates the same type of output, but instead of choosing a smart move, it chooses a move at random.
Here, the input parameter chooser is set to chooser=random.choice during normal game play, but during grading, it will be set to some other function that selects a move in a non-random fashion. Use this function as if it were equivalent to random.choice.
import submitted, importlib
importlib.reload(submitted)
help(submitted.random)
III. Assignment¶
For this assignment, you will need to write three functions: minimax and alphabeta. The content of these functions is described in the sections that follow.
III.A minimax search¶
For Part 1 of this assignment, you will implement minimax search. Specifically, you will implement a function minimax(side, board, flags, depth) in search.py with the following docstring:
importlib.reload(submitted)
help(submitted.minimax)
As you can see, the function accepts side, board, and flags variables, and a non-negative integer, depth. It should perform minimax search over all possible move sequences of length depth, and return the complete tree of evaluated moves as moveTree. If side==True, you should choose a path through this tree that minimizes the heuristic value of the final board, knowing that your opponent will be trying to maximize value; conversely if side==False. Return the resulting optimal list of moves (including moves by both white and black) as moveList, and the numerical value of the final board as value.
A note about depth: The depth parameter specifies the total number of moves, including moves by both white and black. If depth==1 and side==False, then you should just find one move, from the current board, that maximizes the value of the resulting board. If depth==2 and side==False, then you should find a white move, and the immediate following black move. If depth==3 and side==False, then you should find a white, black, white sequence of moves. For example, see wikipedia's page on minimax for examples and pseudo-code.
You are strongly encouraged to look at the grading examples in the grading_examples folder, to get a better understanding of what the minimax function outputs should look like. For example, the board game in more grading_examples/minimax_game0_depth2.json contains value on the first line, moveList on the second line, and moveTree on the third line:
import json, pprint
with open("grading_examples/minimax_game0_depth2.json","r") as f:
value=json.loads(f.readline())
print("value is",value,"\n")
moveList=json.loads(f.readline())
print("moveList is",moveList,"\n")
moveTree=json.loads(f.readline())
print("moveTree is:",moveTree,"\n")
You will certainly want to implement minimax as a recursive function. You will certainly want to use the function generateMoves to generate all moves that are legal in the current game state, and you will certainly want to use makeMove to find the newside, newboard, and newflags that result from making each move. When you get to depth==0, you will certainly want to use evaluate(board) in order to compute the heuristic value of the resulting board.
Once you have implemented minimax, you can test it by playing against it. If you have pygame installed, the following line should pop up a board on which you can play against your own minimax player. If you have not yet written minimax, the game will throw a NotImplementedError when it is white's turn to move.
!python3 main.py --player1 minimax
Test that it is working correctly by moving one of your knights forward. The computer should respond by moving one of its knights foward, as shown here:
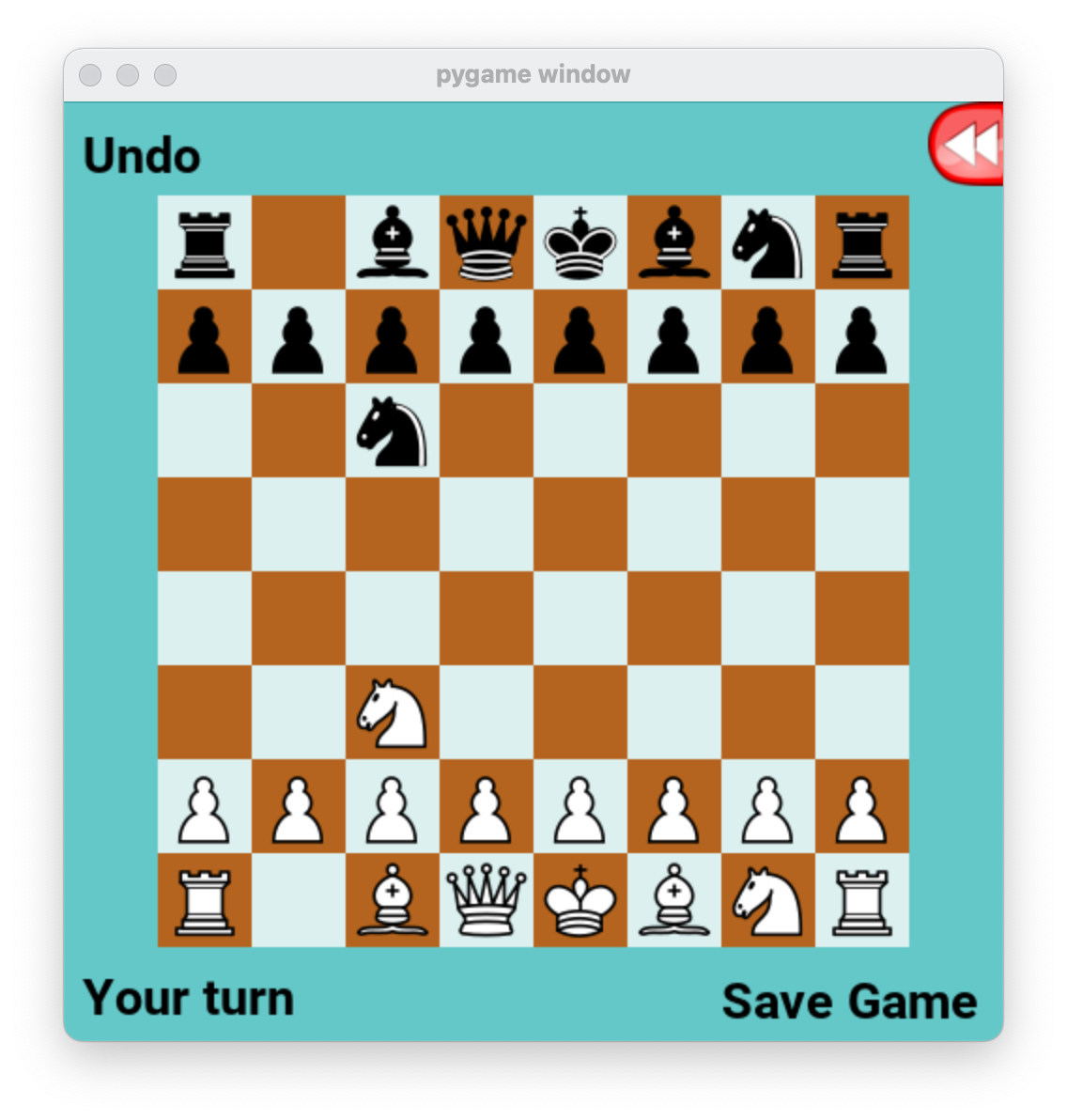
If you want to watch a minimax agent win against a random-move agent, you can type
!python3 main.py --player0 minimax --player1 random
III.B alphabeta search¶
For Part 2 of this assignment, you will implement alphabeta search. Specifically, you will implement a function alphabeta(side, board, flags, depth) in search.py with the following docstring:
import submitted
help(submitted.alphabeta)
For any given input board, this function should return exactly the same value and moveList as minimax; the only difference between the two functions will be the returned moveTree. The tree returned by alphabeta should have fewer leaf nodes than the one returned by minimax, because alphabeta pruning should make it unnecessary to evaluate some of the leaf nodes.
You can test this using:
!python3 main.py --player0 random --player1 alphabeta
IV. Extra Credit¶
The heuristic we've been using, until now, is the default PyChess heuristic: it assigns a value to each piece, with extra points added or subtracted depending on the piece's location. For extra credit, if you wish, you can try to train a neural network to compute a better heuristic.
IV.A. The Game¶
The extra credit assignment will be graded based on how often your heuristic beats the default PhChess heuristic in a two-player game.
Ideally, the game would be chess. Unfortunately, grading your heuristic based on complete chess games would take too much time. Instead, the function extracredit_grade.py plays a very simple game:
- Each of the two players is given the same chess board. Each of you assigns a numerical value to the board.
- Then, the scoring program finds the depth-two minimax value of the same board. This value is provided in the lists called "values" in the data files
extracredit_train.txtandextracredit_validation.txt; but if you have already completed the main assignment, it should be the same value that you'd get by running yourminimaxoralphabetasearch withdepth=2. - The winner of the game is the player whose computed value is closest to the reference value.
Notice that what we're asking you to do, basically, is to create a neural network that can guess the value of the PyChess heuristic two steps ahead.
Notice that, if you can design a funny neural net architecture that, instead of being trained to solve this problem, solves it without training by exactly computing a two-step minimax operation, then you're done. This is explicitly allowed, because we think it would be a very effective and very interesting solution.
Most of you, we guess, will choose a more general neural net architecture, and train it so that it imitates the results of two-step minimax.
IV.B. Distributed Code: Exactly Reproduce the PyChess Heuristic¶
You will find the following files for the extra credit:
- extracredit.py: Trains the model. This is the code you will edit and submit.
- extracredit_embedding.py: Embeds a chess board into a (15x8x8) binary pytorch tensor.
- extracredit_train.txt: Training data: sequences of moves, and corresponding values.
- extracredit_validation.txt: Validation data: sequences of moves, and corresponding values.
- extracredit_grade.py: The grading script.
Try the following:
!python3 extracredit.py
What just happened? Well, if you open extracredit.py you will find these lines:
# Well, you might want to create a model a little better than this...
model = torch.nn.Sequential(torch.nn.Flatten(),torch.nn.Linear(in_features=8*8*15, out_features=1))
# ... and if you do, this initialization might not be relevant any more ...
model[1].weight.data = initialize_weights()
model[1].bias.data = torch.zeros(1)
# ... and you might want to put some code here to train your model:
trainset = ChessDataset(filename='extracredit_train.txt')
trainloader = torch.utils.data.DataLoader(trainset, batch_size=1000, shuffle=True)
for epoch in range(100):
for x,y in trainloader:
pass # Replace this line with some code that actually does the training
# ... after which, you should save it as "model_ckpt.pkl":
torch.save(model, 'model_ckpt.pkl')
The torch.nn.Sequential line has flattened the input board embedding, and then multiplied it by a matrix. The function initialize_weights() initializes that matrix to be exactly equal to the weights used in the PyChess linear heuristic. If you look closely at the training part of the code, you will see that it has done nothing at all; this part of the code is only here to show you how the ChessDataset and DataLoader can be used. After the pass, you see that the model, initialized but not trained, has been saved to model_ckpt.pkl.
IV.C. Leaderboard¶
Now that you've saved model_ckpt.pkl, you can score it using extracredit_grade.py:
!python3 extracredit_grade.py
The leaderboard section shows two separate scores:
winratio_validationis the fraction, of the 1000 boards inextracredit_validation.txt, in which your neural net beat the PyChess heuristic.winratio_evaluationis the same thing, but for the boards inextracredit_evaluation.txtwhich you shouldn't have access to. This is used for final grading with the autograder and will always be -1 locally.
IV.D. Extra Credit Grade¶
Your extra credit grade is given by the variable score in the output from extracredit_grade.py. It is calculated as
score =(2 * (grade_ratio >= 0.5)) + 100 * min(0.08, max(grade_ratio - 0.5, 0))
where grade_ratio is either winratio_validation or winratio_evaluation depending on whether you are grading locally or on gradescope. You will get 2 points for getting winratio = 0.5 and full 10 points if you can get winratio higher than 0.58.
Note: Final grade is determined by the score on gradescope which will be different from local score due to the difference in validation and evaluation set. Local score is for your reference only.
IV.E. Submission Instructions¶
Your file extracredit.py must create a pytorch torch.nn.Module object, and then save it in a file called model_ckpt.pkl.
Pre-trained models (of any interestingly large size) cannot be uploaded to Gradescope, so your model will have to be created, trained, and saved by the file extracredit.py.
You are strongly encouraged to load extracredit_train.txt and/or extracredit_validation.txt in your extracredit.py function.
In order to allow you to train interesting neural nets, we've set up Gradescope to allow you up to 40 minutes of CPU time (on one CPU). It is possible to get full points for this extra credit assignment in three or four minutes of training, but some of you may want to experiment with bigger models.
Warning: Hard to beat alpha-beta!¶
The extra credit thresholds are set so that you can get all of the points if you do well enough on the training data, even if your result is massively overtrained and doesn't generalize well to validation or evaluation data. That's because it's actually really hard to find a neural model that beats alpha-beta by any significant margin. Deep Blue did not use a neural network explicitly, though it had a number of parameters in its evaluation function that were trained using machine-learning-like techniques.
V. Grade your homework¶
Submit the main part of this assignment by uploading submitted.py to Gradescope. You can upload other files with it, but only submitted.py will be retained by the autograder.
Submit the extra credit part of this assignment by uploading extracredit.py to Gradescope. You can upload other files with it, but only extracredit.py will be retained by the autograder.