1 Terrain Generation

Many basic terrain modeling algorithms employ something called Perlin noise to create a highly detailed natural appearance. Invented by Ken Perlin in 1982 while working on the movie Tron, Perlin noise uses randomness and repetition to synthesize 2D and 3D textures. In 1997, Perlin won an Academy Award for Technical Achievement from the Academy of Motion Picture Arts and Sciences for this contribution to graphics. Perlin noise and techniques based off of it are still widely used in games and movies today.

Realistic terrain generation in modern games require tools that do more than just model the basic underlying terrain…these tools support operations like creation of vegetation and roads and erosion. See this talk by Ubisoft developer Etienne Carrier if you are interested in seeing the tools technical artists use these days.

2 The Faulting Method

The same year (1982) that Ken Perlin crated Perlin Noise, Benoit Mandelbrot proposed a less efficient but easier-to-implement method called the faulting method.

In addition to this page, you can find a summary of the faulting method in section 3.1.2 of the following survey paper on terrain generation algorithms:

A Review of Digital Terrain Modeling. Eric Galin, Eric Guérin, Adrien Peytavie, et al. [PDF]

The overall faulting method process runs as follows:

1. Create a triangulated 2D grid
2. Repeatedly
   1. Pick a random vertical plane, called a fault plane
   2. Move points on one side of the fault plane up and points on the other side of the fault plane down by some small increment
3. Compute the vertex normals

2.1 Creating a grid

2.1.1 Rectangular grids

An n \times n rectangular grid of points like this:

can be joined into triangles by one of two ways of splitting the squares;

• either join (i, i+1, i+n) and (i+1, i+n, i+n+1)

• or join (i, i+1, i+n+1) and (i+n+1, i+n, i)

Rectangular grids are easy to define, but because of the longer diagonal compared to shorter edges the chosen axes can be visually noticeable in some situations.

2.1.2 Hexagonal grids

Triangular or hexagonal grids can be created by modifying the rectangualr grid creation as follows:

1. Move each row over by ½ compared to the row before it
2. Reduce row separation by a factor of \sqrt{3} / 2
3. The result is a sheered rectangle
   • to make it hexagonal, omit a point with row and column indices (r,c) if (r + c) < \frac{n}{2} or (r+c) > \frac{3n}{2}
   • to make it triangular, omit a point with row and column indices (r,c) if (r + c) > n

2.2 Random fault planes

We will construct a fault plane cutting through the terrain by generating a random point p and random direction vector \vec{n} to define the plane.

1. First generate a random point p in the (x,y) bounds of the grid.
2. Generate a random normal vector \vec{n} with z = 0 for the plane; in other words, (x_n,y_n,0), where x_n,y_n is a point uniformly sampled on the unit circle. If \theta is a random angle between 0 and 2\pi then an appropriate random normal would be \vec{n}=(\cos{\theta},\sin{\theta},0).

Then for each vertex b,

1. Test which side of the plane that vertex falls on by using the dot product test (b-p) \cdot n \ge 0.

   

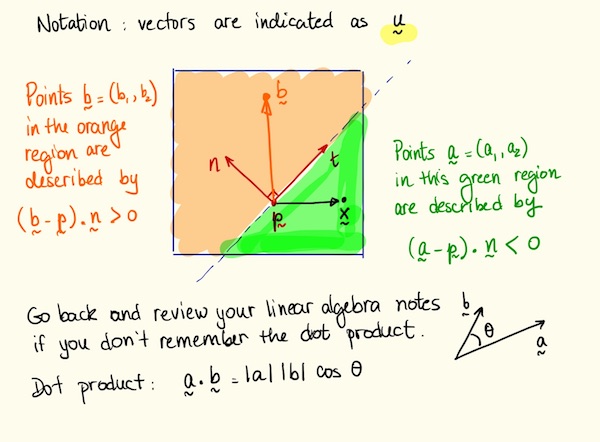
2. If b is in the negative half-space, lower the z coordinate of by some amount \Delta. If b is in the positive half-space, raise the z coordinate of by some amount \Delta.

   Optional You may get better results with distance weighted displacements for \Delta, only moving vertices that are relatively close to the faulting plane. To do so compute the distance r=\mathbf{d}(b,\Phi_i) from b to the fault plane \Phi_i and alter the \Delta you use for each vertex by a coefficient function g(r)=(1-(r/R)^2)^2 for r<R and g(r)=0 elsewhere. R is a parameter you determine.

This algorithm works best if early faults have large displacements and later faults have smaller ones. A simple way to achieve this is to scale \Delta down each iteration by some scaling factor between 0 and 1.

Once you’re done, you might need to re-scale the vertical axis to get the desired ratio between vertical displacement and horizontal size.

2.3 Compute vertex normals

The cross product of any pair of edge vectors of a triangle is (a) normal to the triangle and (b) has a length proportional to the triangle’s area. But depending on which two points you pick, it might be pointing in either direction: either out of or in to the surface the triangle is part of.

A reasonable way to compute a vertex normal is as an area-weighted average of the face normals of its adjacent faces: in other words, the sum of those cross-product-generated vectors.

Thus, we can find the vertex normals by

1. Initialize a zero-vector for every vertex

2. Loop over every triangle, and for each

   1. Find two edge vectors, p_2-p_0 and p_1-p_0

   2. Take the cross product of the edge vectors

      What if it points the wrong way? Ideally we’d define the triangles carefully so it never does, but for terrain we can also fix it: if the z component is negative, negate the vector.

   3. Add the vector to all three vertex’s normals

3. Normalize all the resulting normal vectors.

   For best performance, normalize them in JavaScript if they won’t change frame to frame, in the vertex shader if they will.

   Don’t forget to also normalize them in your fragment shader! Normalizing per vertex keeps longer normals from dominating the interpolation; normalizing per fragment corrects for the shortening that happens during interpolation.