In this MP you will
- Generate a sphere with any number of latitude and longitude points
- Generate a torus with any number of rings and slices
This MP is elective, with no core components. It assumes you have already completed the Terrain MP.
1 Overview
You will submit a webpage that has
- Two number entry fields
- One checkbox field
- One button
- One canvas
- A 3D view of dynamically-generated fractal terrain
Submit an HTML file and any number of js, glsl, and css files. No image or JSON files are permitted for this assignment.
You are welcome to use a JavaScript math library, such as the one used in in-class examples or others you might know.
2 Specification
2.1 HTML input setup
Have one input numeric field for entering a number of rings in the generated object. Rings are latitude lines on a sphere (like the equator) and encircle the opening of a torus. The poles of a sphere do not count as rings, so a 1-ring sphere has the equator and two poles.
Have one input numeric field for entering a number of slices in the generated object. Slices are longitude lines on a sphere (like the prime meridian) and pass through the hole of a torus.
Optionally, Have one checkbox for selecting between sphere and torus. If you do not have this, or have it but don’t generate both geometry types upon request, you will get at most half credit on this MP.
HTML input elements, styling, and event handling are beyond the scope of this class. See the Terrain MP for example code for setting up inputs. The checkbox can be added with this HTML:
<label>Torus: <input id="torus" type="checkbox"/></label>and this JavaScript:
const torus = document.querySelector('#torus').checked2.2 Generate a sphere
When the button is clicked and the torus checkbox is not checked, generate a sphere.
Position the vertices so that edges form latitude and longitude lines
around the sphere. Support any number of rings ≥ 1 and any number of
slices ≥ 3. As a simple check, if you use 1 latitude ring and 4 slices,
you should get the Platonic solid called an octahedron.
We recommend computing the surface normals exactly: the surface normal of a point on a sphere points directly away from the center of that sphere. For a unit-radius sphere centered at the origin, that means that \vec n = \mathbf{p}. If you don’t compute them exactly make sure you don’t have any visible creases or seams, especially near the poles and equator.
When generating a sphere with r rings and s slices you should end up with exactly 2+rs vertices and 2rs triangles.
2.3 Generate a torus
When the button is clicked and the torus checkbox is checked, generate a torus.
Position the vertices so that edges form a grid over the torus with some edge chains circling the entire torus and others passing through its center.
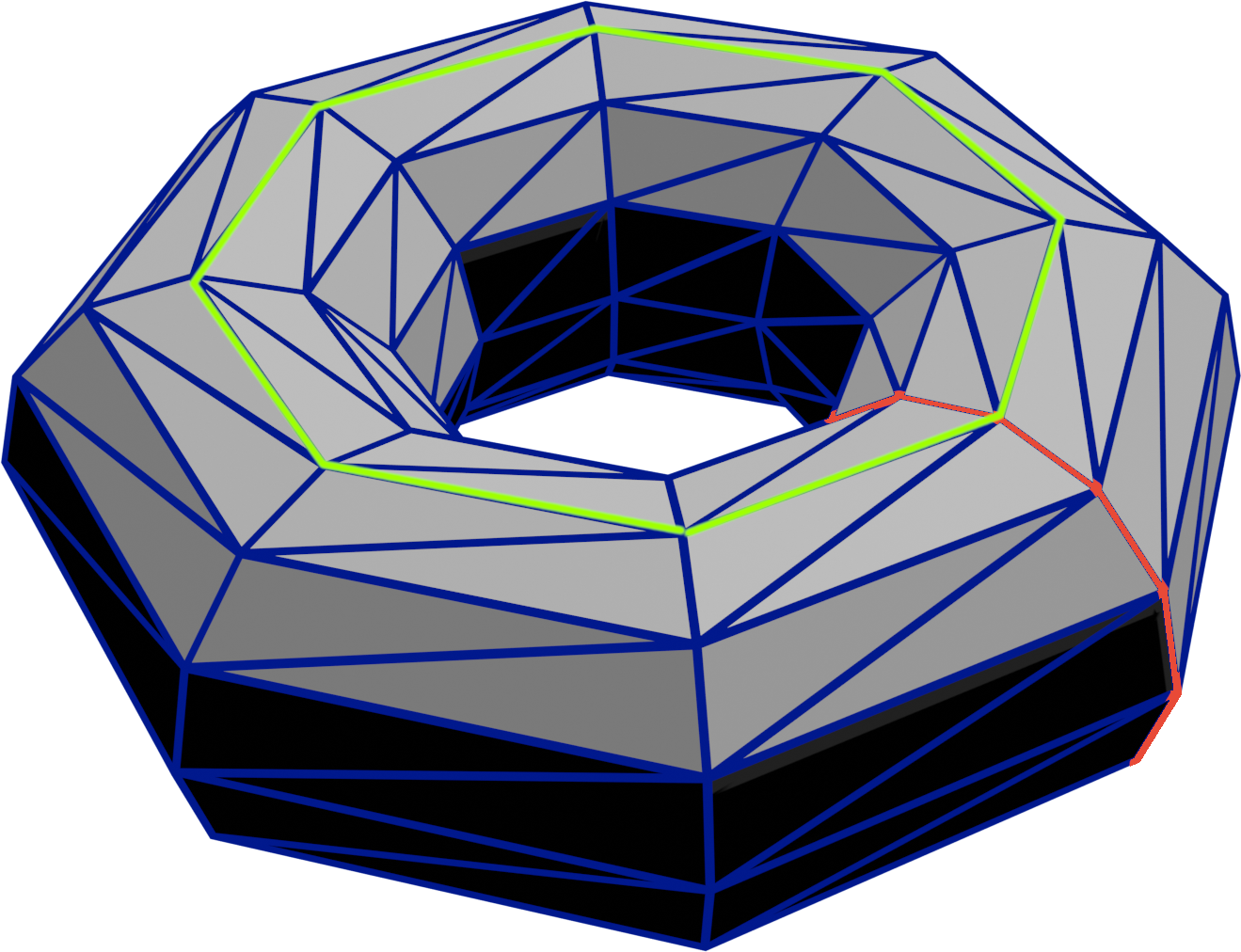
Support any number of rings ≥ 3 and any number of slices ≥ 3.
We recommend computing the surface normals exactly: the surface normal of a point on a torus points directly away from the center of ring at that part of the torus. If you don’t compute them exactly make sure you don’t have any visible creases or seams.
When generating a sphere with r rings and s slices you should end up with exactly rs vertices and 2rs triangles.
2.4 Render and light
Render the geometry with both diffuse and specular lighting. Have the camera moving around the geometry.
3 Evaluating your results
On both your development machine and when submitted to the submission server and then viewed by clicking the HTML link, the resulting page should initially be blank. Once the button is pressed a sphere or torus should appear, filling most of the screen with a moving camera. One example might be the following:
If your submission only generates spheres, or only toruses, you’ll get half the points. Points will be deducted if you generate more vertices or triangles than the shape being generated requires.